So verwenden Sie die t-Verteilung in Python

Die t-Verteilung ist eine Wahrscheinlichkeitsverteilung, die der Normalverteilung ähnlich ist, außer dass sie stärkere Seiten als die Normalverteilung hat.

Das heißt, im Vergleich zur Normalverteilung befinden sich mehr Werte in der Verteilung an den Enden als in der Mitte:

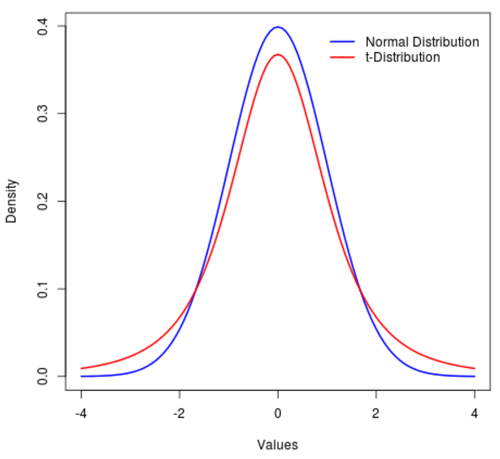
Dieses Tutorial erklärt, wie man die t-Verteilung in Python verwendet.

So generieren Sie bei der Verteilung

Sie können die Funktion t.rvs(df, size) verwenden, um Zufallswerte aus einer t-Verteilung mit einem bestimmten Freiheitsgrad und Stichprobenumfang zu generieren:

from scipy.stats import t

#Generiere Zufallswerte aus der t-Verteilung mit df=6 und Stichprobengröße=10
t.rvs(df=6, size=10)

array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611,
       -0.45384974, -0.2767931 , -0.40177789, -0.3602592 ,  0.38262431])

Das Ergebnis ist ein Array von 10 Werten, die bei einer Verteilung mit 6 Freiheitsgraden folgen.

So berechnen Sie p-Werte mithilfe der t-Verteilung

Wir können die Funktion t.cdf(x, df, loc=0, scale=1) verwenden, um den p-Wert zu finden, der mit einer t-Teststatistik verknüpft ist.

Beispiel 1: Finden Sie den einseitigen P-Wert

Angenommen, wir führen einen einseitigen Hypothesentest durch und erhalten am Ende eine Teststatistik von -1,5 und Freiheitsgrade = 10.

Wir können die folgende Syntax verwenden, um den p-Wert zu berechnen, der dieser Teststatistik entspricht:

from scipy.stats import t

#p-Wert berechnen
t.cdf(x=-1.5, df=10)

0.08225366322272008

Der einseitige p-Wert, der einer Teststatistik von -1,5 mit 10 Freiheitsgraden entspricht, beträgt 0,0822.

Beispiel 2: Finden Sie den zweiseitigen P-Wert

Angenommen, wir führen einen zweiseitigen Hypothesentest durch und erhalten am Ende eine Teststatistik von 2,14 und Freiheitsgrade = 20.

Wir können die folgende Syntax verwenden, um den p-Wert zu berechnen, der dieser Teststatistik entspricht:

from scipy.stats import t

#p-Wert berechnen
(1 - t.cdf(x=2.14, df=20)) * 2

0.04486555082549959

Der zweiseitige p-Wert, der einer Teststatistik von 2,14 mit 20 Freiheitsgraden entspricht, beträgt 0,0448.

Hinweis: Sie können diese Antworten mit dem Rechner für die inverse t-Verteilung überprüfen.

Wie man bei der Verteilung zeichnet

Sie können die folgende Syntax verwenden, um die Verteilung mit bestimmten Freiheitsgraden darzustellen:

from scipy.stats import t
import matplotlib.pyplot as plt

#Erzeuge eine t-Verteilung mit einer Stichprobengröße von 10000
x = t.rvs(df=12, size=10000)

# Diagramm der t-Verteilung erstellen
plt.hist(x, density=True, edgecolor='black', bins=20)

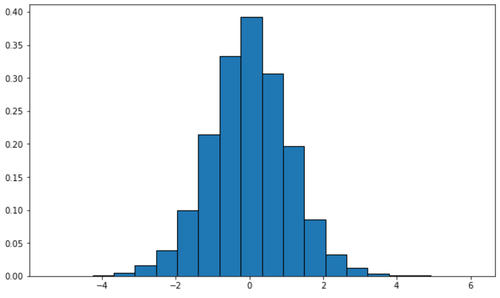
Alternativ können Sie eine Dichtekurve mit dem Seaborn-Visualisierungspaket erstellen:

import seaborn as sns

#Dichtekurve erstellen
sns.kdeplot(x)

Zusätzliche Ressourcen

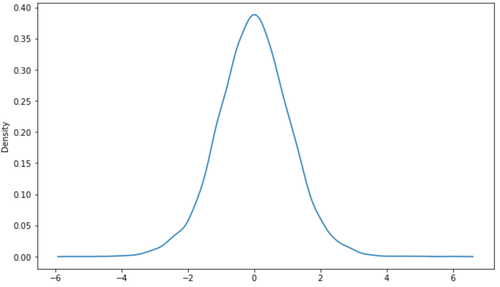
Die folgenden Tutorials bieten zusätzliche Informationen zur t-Verteilung:

Rechner für die inverse t-Verteilung