Eine einfache Einführung in Random Forests

Wenn die Beziehung zwischen einer Reihe von Prädiktorvariablen und einer Antwortvariablen sehr komplex ist, verwenden wir häufig nichtlineare Methoden, um die Beziehung zwischen ihnen zu modellieren.

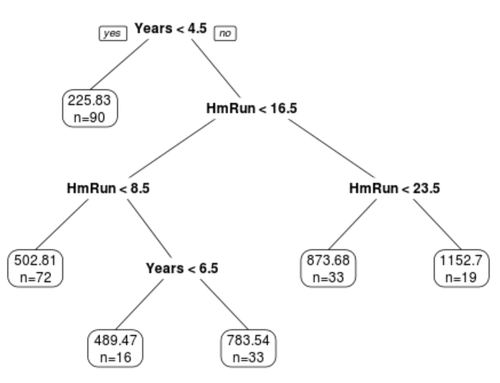
Eine solche Methode sind Klassifikations- und Regressionsbäume, die eine Reihe von Prädiktorvariablen verwenden, um Entscheidungsbäume zu erstellen, die den Wert einer Antwortvariablen vorhersagen.

Der Vorteil von Entscheidungsbäumen besteht darin, dass sie leicht zu interpretieren und zu visualisieren sind. Die Verkleinerung besteht darin, dass sie tendenziell unter einer hohen Varianz leiden. Das heißt, wenn wir einen Datensatz in zwei Hälften teilen und einen Entscheidungsbaum auf beide Hälften anwenden, können die Ergebnisse sehr unterschiedlich sein.

Eine Möglichkeit, die Varianz von Entscheidungsbäumen zu verringern, besteht in der Verwendung einer als Bagging bezeichneten Methode, die wie folgt funktioniert:

1. Nehmen Sie b Bootstrap-Proben aus dem Originaldatensatz.

2. Erstellen Sie einen Entscheidungsbaum für jedes Bootstrap-Beispiel.

3. Berechnen Sie den Durchschnitt der Vorhersagen jedes Baums, um ein endgültiges Modell zu erhalten.

Der Vorteil dieses Ansatzes besteht darin, dass ein Bagged-Modell in der Regel eine Verbesserung der Testfehlerrate im Vergleich zu einem einzelnen Entscheidungsbaum bietet.

Der Nachteil ist, dass die Vorhersagen aus der Sammlung von Bagged-Trees stark korreliert sein können, wenn der Datensatz zufällig einen sehr starken Prädiktor enthält. In diesem Fall verwenden die meisten oder alle Bagged-Trees diesen Prädiktor für die erste Aufteilung, was zu Bäumen führt, die einander ähnlich sind und stark korrelierte Vorhersagen aufweisen.

Wenn wir also die Vorhersagen jedes Baums mitteln, um ein endgültiges Bagged-Modell zu erhalten, ist es möglich, dass dieses Modell die Varianz im Vergleich zu einem einzelnen Entscheidungsbaum nicht wesentlich reduziert.

Eine Möglichkeit, dieses Problem zu umgehen, ist die Verwendung einer Methode, die als zufällige Gesamtstrukturen bezeichnet wird.

Was sind Random Forests?

Ähnlich wie beim Bagging nehmen Random Forests auch b Bootstrap-Proben aus einem Originaldatensatz.

Wenn jedoch ein Entscheidungsbaum für jede Bootstrap-Stichprobe erstellt wird, wird jedes Mal, wenn eine Teilung in einem Baum berücksichtigt wird, nur eine zufällige Stichprobe von m Prädiktoren als Teilungskandidaten aus dem vollständigen Datensatz von p Prädiktoren betrachtet.

Hier ist die vollständige Methode, mit der zufällige Gesamtstrukturen ein Modell erstellen:

1. Nehmen Sie b Bootstrap-Proben aus dem Originaldatensatz.

2. Erstellen Sie einen Entscheidungsbaum für jedes Bootstrap-Beispiel.

• Beim Erstellen des Baums wird jedes Mal, wenn eine Teilung berücksichtigt wird, nur eine zufällige Stichprobe von m Prädiktoren als Teilungskandidaten aus dem vollständigen Datensatz von p Prädiktoren betrachtet. 3. Durchschnitt der Vorhersagen jedes Baums, um ein endgültiges Modell zu erhalten.

Mit dieser Methode wird die Sammlung von Bäumen in einem Random Forest dekorrelierten im Vergleich zu den durch Bagging erzeugten Bäume.

Wenn wir also die durchschnittlichen Prädikationen jedes Baums verwenden, um ein endgültiges Modell zu erhalten, weist dieser tendenziell eine geringere Variabilität auf und führt zu einer geringeren Testfehlerrate im Vergleich zu einem verpackten Modell.

Bei der Verwendung zufälliger Gesamtstrukturen betrachten wir m = √ p-Prädiktoren normalerweise jedes Mal als geteilte Kandidaten, wenn wir einen Entscheidungsbaum teilen.

Wenn wir beispielsweise p = 16 Gesamtprädiktoren in einem Datensatz haben, betrachten wir normalerweise nur m = √16 = 4 Prädiktoren als potenzielle Split-Kandidaten bei jedem Split.

Technischer Hinweis: Es ist interessant festzustellen, dass wenn wir m = p wählen (d.h. alle Prädiktoren bei jedem Split als Split-Kandidaten betrachten), dies der einfachen Verwendung von Bagging entspricht.

Out-of-Bag-Fehlerschätzung

Ähnlich wie beim Bagging können wir den Testfehler eines Random Forest-Modells mithilfe der Out-of-Bag-Schätzung berechnen.

Es kann gezeigt werden, dass jedes Bootstrap-Beispiel etwa 2/3 der Beobachtungen aus dem Originaldatensatz enthält. Das verbleibende Drittel der Beobachtungen, die nicht zur Anpassung an den Baum verwendet wurden, werden als OOB-Beobachtungen (Out-of-Bag) bezeichnet.

Wir können den Wert für die i-te Beobachtung im Originaldatensatz vorhersagen, indem wir die durchschnittliche Vorhersage von jedem der Bäume nehmen, in denen diese Beobachtung OOB war.

Mit diesem Ansatz können wir eine Vorhersage für alle n Beobachtungen im Originaldatensatz erstellen und so eine Fehlerrate berechnen, die eine gültige Schätzung des Testfehlers darstellt.

Der Vorteil dieses Ansatzes zur Schätzung des Testfehlers besteht darin, dass er viel schneller als die k-fache Kreuzvalidierung ist, insbesondere wenn der Datensatz groß ist.

Die Vor- und Nachteile von Random Forests

Vorteile:

• In den meisten Fällen bieten Random Forests eine Verbesserung der Genauigkeit im Vergleich zu Bagging-Modellen und insbesondere im Vergleich zu Einzelentscheidungsbäumen.
• Random Forests sind robust gegenüber Ausreißern.
• Für die Verwendung zufälliger Gesamtstrukturen ist keine Vorverarbeitung erforderlich.

Nachteile:

• Sie sind schwer zu interpretieren.
• Sie können rechenintensiv (d.h. langsam) sein, um auf großen Datenmengen aufzubauen. In der Praxis verwenden Datenwissenschaftler normalerweise zufällige Gesamtstrukturen, um die Vorhersagegenauigkeit zu maximieren, sodass die Tatsache, dass sie nicht leicht zu interpretieren sind, normalerweise kein Problem darstellt.