Einführung in die multiple lineare Regression

Wenn wir die Beziehung zwischen einer einzelnen Prädiktorvariablen und einer Antwortvariablen verstehen wollen, verwenden wir häufig eine einfache lineare Regression.

Wenn wir jedoch die Beziehung zwischen mehreren Prädiktorvariablen und einer Antwortvariablen verstehen möchten, können wir stattdessen multiple lineare Regressionen verwenden.

Wenn wir p Prädiktorvariablen haben, hat ein multiples lineares Regressionsmodell die Form:

Y = β ₀ + β ₁ X ₁ + β ₂ X ₂ +… + β _p X _p + ε

wo:

• Y: Die Antwortvariable
• X _j: Die j-te Prädiktorvariable
• β _j: Der durchschnittliche Effekt einer Zunahme von X _{j um} eine Einheit auf Y, wobei alle anderen Prädiktoren festgehalten werden
• ε: Der Fehlerterm

Die Werte für β ₀ , β ₁ , B ₂ ,…, β _p werden nach der Methode der kleinsten Quadrate ausgewählt, die die Summe der quadratischen Residuen (RSS) minimiert:

RSS = Σ (y _i - ŷ _i ) ²

wo:

• Σ: Ein griechisches Symbol, das Summe bedeutet
• y _i: Der tatsächliche Antwortwert für die i-te Beobachtung
• ŷ _i: Der vorhergesagte Antwortwert basierend auf dem multiplen linearen Regressionsmodell

Die Methode zur Ermittlung dieser Koeffizientenschätzungen basiert auf der Matrixalgebra, auf die hier nicht näher eingegangen wird. Glücklicherweise kann jede statistische Software diese Koeffizienten für Sie berechnen.

Interpretieren der Ausgabe mehrerer linearer Regressionen

Angenommen, wir passen ein Modell mit mehreren linearen Regressionen an, indem wir die untersuchten Stunden der Prädiktorvariablen und die vorbereitenden Prüfungen sowie die Prüfungsergebnisse der Antwortvariablen verwenden.

Der folgende Screenshot zeigt, wie die Ausgabe der multiplen linearen Regression für dieses Modell aussehen könnte:

Hinweis: Der folgende Screenshot zeigt multiple lineare Regressionsausgaben für Excel. Die in der Ausgabe angezeigten Zahlen sind jedoch typisch für die Regressionsausgaben, die Sie mit einer statistischen Software sehen.

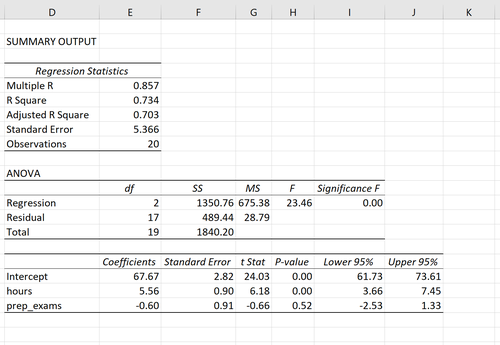
Aus den Modellausgaben ermöglichen die Koeffizienten die Bildung eines geschätzten multiplen linearen Regressionsmodells:

Prüfungsergebnis = 67,67 + 5,56 * (Stunden) - 0,60 * (Vorbereitungsprüfungen)

Die Interpretation der Koeffizienten erfolgt wie folgt:

• Jede zusätzliche Erhöhung der untersuchten Stunden um eine Einheit ist mit einer durchschnittlichen Erhöhung der Prüfungspunktzahl um 5,56 Punkte verbunden, vorausgesetzt, die Vorbereitungsprüfungen werden konstant gehalten.
• Jede zusätzliche Erhöhung der vorbereiteten Prüfungen um eine Einheit ist mit einer durchschnittlichen Abnahme der Prüfungsergebnisse um 0,60 Punkte verbunden, vorausgesetzt, die untersuchten Stunden werden konstant gehalten.

Wir können dieses Modell auch verwenden, um die erwartete Prüfungspunktzahl zu ermitteln, die ein Schüler auf der Grundlage seiner gesamten Stunden und der vorbereiteten Prüfungen erhält. Zum Beispiel wird von einem Studenten, der 4 Stunden studiert und 1 Vorbereitungsprüfung ablegt, erwartet, dass er bei der Prüfung 89,31 Punkte erzielt:

Prüfungsergebnis = 67,67 + 5,56 * (4) -0,60 * (1) = 89,31

So interpretieren Sie das Residuum der Modellausgabe:

• R-Quadrat: Dies ist als Bestimmungskoeffizient bekannt. Es ist der Anteil der Varianz in der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann. In diesem Beispiel lassen sich 73,4% der Abweichungen in den Prüfungsergebnissen durch die Anzahl der untersuchten Stunden und die Anzahl der vorbereiteten Prüfungen erklären.
• Standardfehler: Dies ist der durchschnittliche Abstand, um den die beobachteten Werte von der Regressionslinie fallen. In diesem Beispiel fallen die beobachteten Werte durchschnittlich um 5,366 Einheiten von der Regressionslinie ab.
• F: Dies ist die Gesamt-F-Statistik für das Regressionsmodell, berechnet als Regressions-MS / Residuen-MS.
• Bedeutung F: Dies ist der p-Wert, der der gesamten F-Statistik zugeordnet ist. Es zeigt uns, ob das Regressionsmodell insgesamt statistisch signifikant ist oder nicht. Mit anderen Worten, es sagt uns, ob die beiden erklärenden Variablen zusammen eine statistisch signifikante Assoziation mit der Antwortvariablen haben. In diesem Fall beträgt der p-Wert weniger als 0,05, was darauf hinweist, dass die erklärenden Variablen Stunden, die untersucht und Vorbereitungsprüfungen kombiniert wurden, eine statistisch signifikante Assoziation mit dem Prüfungsergebnis aufweisen.
• Koeffiziente P-Werte. Die einzelnen p-Werte geben Auskunft darüber, ob jede erklärende Variable statistisch signifikant ist oder nicht. Wir können sehen, dass die untersuchten Stunden statistisch signifikant sind (p = 0,00), während die durchgeführten Vorbereitungsprüfungen (p = 0,52) bei α = 0,05 statistisch nicht signifikant sind. Da die vorbereiteten Prüfungen statistisch nicht signifikant sind, entscheiden wir uns möglicherweise, sie aus dem Modell zu entfernen.

So bewerten Sie die Anpassung eines multiplen linearen Regressionsmodells

Es gibt zwei Zahlen, die häufig verwendet werden, um zu bewerten, wie gut ein multiples lineares Regressionsmodell zu einem Datensatz passt:

1. R-Quadrat: Dies ist der Anteil der Varianz in der Antwortvariablen, der durch die Prädiktorvariablen erklärt werden kann.

Der Wert für R-Quadrat kann im Bereich von 0 bis 1 liegen. Ein Wert von 0 zeigt an, dass die Antwortvariable überhaupt nicht durch die Prädiktorvariable erklärt werden kann. Ein Wert von 1 gibt an, dass die Antwortvariable durch die Prädiktorvariable fehlerfrei perfekt erklärt werden kann.

Je höher das R-Quadrat eines Modells ist, desto besser kann das Modell die Daten anpassen.

2. Standardfehler: Dies ist der durchschnittliche Abstand, um den die beobachteten Werte von der Regressionslinie fallen. Je kleiner der Standardfehler ist, desto besser kann ein Modell die Daten anpassen.

Wenn wir Vorhersagen mithilfe eines Regressionsmodells treffen möchten, kann der Standardfehler der Regression eine nützlichere Metrik sein als das R-Quadrat, da er uns eine Vorstellung davon gibt, wie genau unsere Vorhersagen in Einheiten sein werden.

In den folgenden Artikeln finden Sie eine vollständige Erläuterung der Vor- und Nachteile der Verwendung von R-Quadrat im Vergleich zum Standardfehler zur Beurteilung der Modellanpassung:

• Was ist ein guter R-Quadrat-Wert?
• Grundlegendes zum Standardfehler eines Regressionsmodells

Annahmen der multiplen linearen Regression

Es gibt vier Hauptannahmen, die die multiple lineare Regression für die Daten macht:

1. Lineare Beziehung: Es besteht eine lineare Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variablen y.

2. Unabhängigkeit: Die Residuen sind unabhängig. Insbesondere gibt es keine Korrelation zwischen aufeinanderfolgenden Residuen in Zeitreihendaten.

3. Homoskedastizität: Die Residuen weisen auf jeder Ebene von x eine konstante Varianz auf.

4. Normalität: Die Residuen des Modells sind normalverteilt.

Eine vollständige Erklärung zum Testen dieser Annahmen finden Sie in diesem Artikel.

Multiple lineare Regression mit Software

Die folgenden Tutorials enthalten schrittweise Beispiele für die Durchführung einer multiplen linearen Regression mit unterschiedlicher Statistiksoftware/Programmen:

So führen Sie eine mehrfache lineare Regression in R durch
Durchführen einer mehrfachen linearen Regression in Python
Durchführen einer mehrfachen linearen Regression in Excel
Durchführen einer mehrfachen linearen Regression in SPSS
Durchführen einer mehrfachen linearen Regression in Stata
So führen Sie eine lineare Regression in Google Tabellen durch