Eine Einführung in die Binomialverteilung

Die Binomialverteilung ist eine der beliebtesten Verteilungen in der Statistik. Um die Binomialverteilung zu verstehen, ist es hilfreich, zunächst Binomialversuche zu verstehen.

Binomialtests

Ein Binomialtest ist ein Versuch mit folgenden Eigenschaften:

• Der Test besteht aus n wiederholten Versuchen.
• Jeder Versuch hat nur zwei mögliche Ergebnisse.
• Die mit p bezeichnete Erfolgswahrscheinlichkeit ist für jeden Versuch gleich.
• Jeder Versuch ist unabhängig.

Das offensichtlichste Beispiel für einen Binomialtest ist ein Münzwurf. Angenommen, wir werfen 10 Mal eine Münze. Dies ist ein Binomialtest, da es die folgenden vier Eigenschaften aufweist:

• Der Test besteht aus n wiederholten Versuchen – Es gibt 10 Versuche.
• Jeder Versuch hat nur zwei mögliche Ergebnisse – Kopf oder Zahl.
• Die mit p bezeichnete Erfolgswahrscheinlichkeit ist für jeden Versuch gleich. Wenn wir „Erfolg“ als Landung auf dem Kopf definieren, beträgt die Erfolgswahrscheinlichkeit für jeden Versuch genau 0,5.
• Jeder Versuch ist unabhängig – Das Ergebnis eines Münzwurfs hat keinen Einfluss auf das Ergebnis eines anderen Münzwurfs.

Die Binomialverteilung

Die Binomialverteilung beschreibt die Wahrscheinlichkeit, in n Binomialtests k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Wahrscheinlichkeit, dass X = k erfolgreich ist, durch die folgende Formel ermittelt werden:

P(X = k) = _n C _k * P ^k * (1-p) ^nk

wobei:

• n: Anzahl der Versuche
• k: Anzahl der Erfolge
• p: Erfolgswahrscheinlichkeit eines bestimmten Versuchs
• _n C _k: Die Anzahl der Möglichkeiten, k Erfolge in n Versuchen zu erzielen

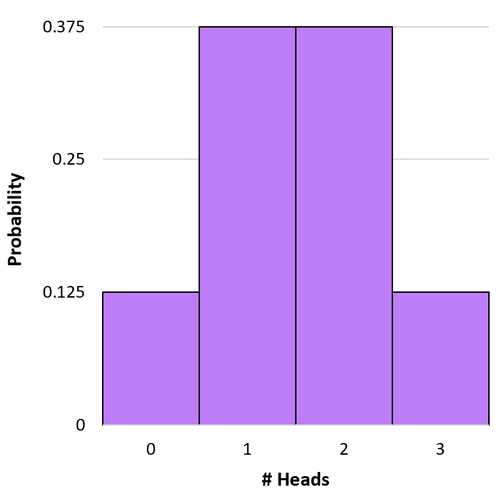
Nehmen wir zum Beispiel an, wir werfen dreimal eine Münze. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, 0, 1, 2 und 3 Köpfe während dieser 3 Flips zu erhalten:

P(X = 0) = ₃ C ₀ * .5 ⁰ * (1-.5) ^3-0 = 1 * 1 * (.5) ³ = 0,125

P(X = 1) = ₃ C ₁ * .5 ¹ * (1-.5) ^3-1 = 3 * .5 * (.5) ² = 0,375

P(X = 2) = ₃ C ₂ · 0,5 ² · (1–5) ^3–2 = 3 · 0,25 · (0,5) ¹ = 0,375

P(X = 3) = ₃ C ₃ * .5 ³ * (1-.5) ^3-3 = 1 * .125 * (.5) ⁰ = 0.125

Wir können ein einfaches Histogramm erstellen, um diese Wahrscheinlichkeitsverteilung zu visualisieren:

Berechnung der kumulativen Binomialwahrscheinlichkeiten

Es ist einfach, eine einzelne Binomialwahrscheinlichkeit (z. B. die Wahrscheinlichkeit, dass eine Münze 1 Mal aus 3 Flips auf den Köpfen landet) mit der obigen Formel zu berechnen. Um jedoch die kumulativen Binomialwahrscheinlichkeiten zu berechnen, müssen einzelne Wahrscheinlichkeiten hinzugefügt werden.

Nehmen wir zum Beispiel an, wir möchten die Wahrscheinlichkeit wissen, dass eine Münze 1 Mal oder weniger aus 3 Flips auf den Köpfen landet. Wir würden die folgende Formel verwenden, um diese Wahrscheinlichkeit zu berechnen:

P( X ≤ 1) = P(X = 0) + P(X = 1) = 0,125 + 0,375 = 0,5.

Dies wird als kumulative Wahrscheinlichkeit bezeichnet, da mehr als eine Wahrscheinlichkeit hinzugefügt werden muss. Wir können die kumulative Wahrscheinlichkeit, k oder weniger Köpfe für jedes Ergebnis zu erhalten, unter Verwendung einer ähnlichen Formel berechnen:

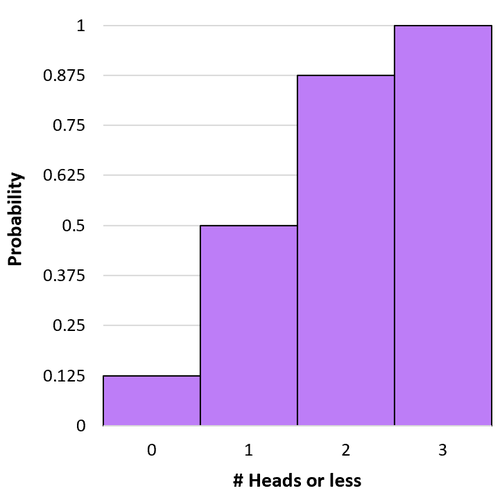
P( X ≤ 0) = P(X = 0) = 0,125.

P( X ≤ 1) = P(X = 0) + P(X = 1) = 0,125 + 0,375 = 0,5.

P( X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0,125 + 0,375 + 0,375 = 0,875.

P( X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0,125 + 0,375 + 0,375 + 0,125 = 1.

Wir können ein Histogramm erstellen, um diese kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

Eigenschaften der Binomialverteilung

Die Binomialverteilung hat folgende Eigenschaften:

Der Mittelwert der Verteilung ist μ = np

Die Varianz der Verteilung beträgt σ ²= np (1-p)

Die Standardabweichung der Verteilung ist σ = √ np (1-p)

Angenommen, wir werfen dreimal eine Münze. Sei p = die Wahrscheinlichkeit, mit der die Münze auf Köpfen landet.

Die mittlere Anzahl von Köpfen, die wir erwarten würden, ist μ = np = 3 * .5 = 1,5.

Die Varianz in der Anzahl der Köpfe, die wir erwarten würden, ist σ ² = np (1-p) = 3 * .5 * (1-.5) = 0,75.

Probleme mit der Binomialverteilung

Verwenden Sie die folgenden Übungsprobleme, um Ihr Wissen über die Binomialverteilung zu testen.

Problem 1

Frage: Bob macht 60% seiner Freiwurfversuche. Wenn er 12 Freiwürfe schießt, wie hoch ist die Wahrscheinlichkeit, dass er genau 10 macht?

Antwort: Unter Verwendung des obigen Binomialverteilungsrechners mit p = 0,6, n = 12 und k = 10 stellen wir fest, dass P(X = 10) = 0,06385 ist.

Problem 2

Frage: Jessica wirft 5 Mal eine Münze. Wie groß ist die Wahrscheinlichkeit, dass die Münze zweimal oder weniger auf den Köpfen landet?

Antwort: Unter Verwendung des obigen Binomialverteilungsrechners mit p = 0,5, n = 5 und k = 2 stellen wir fest, dass P(X ≤ 2) = 0,5 ist.

Problem 3

Frage: Die Wahrscheinlichkeit, dass ein bestimmter Student an einem bestimmten College aufgenommen wird, beträgt 0,2. Wenn sich 10 Studenten bewerben, wie hoch ist die Wahrscheinlichkeit, dass mehr als 4 akzeptiert werden?

Antwort: Unter Verwendung des obigen Binomialverteilungsrechners mit p = 0,2, n = 10 und k = 4 stellen wir fest, dass P(X> 4) = 0,03279 ist.

Problem 4

Frage: Sie werfen 12 Mal eine Münze. Was ist die durchschnittliche erwartete Anzahl von Köpfen, die angezeigt werden?

Antwort: Denken Sie daran, dass der Mittelwert einer Binomialverteilung als μ = np berechnet wird. Somit ist μ = 12 · 0,5 = 6 Köpfe.

Problem 5

Frage: Mark trifft bei 10% seiner Versuche einen Homerun. Wenn er 5 Versuche in einem bestimmten Spiel hat, wie groß ist die Varianz der Anzahl der Home Runs, die er treffen wird?

Antwort: Denken Sie daran, dass die Varianz einer Binomialverteilung als σ² = np(1-p) berechnet wird. Somit ist σ ² = 6 * 0,1 * (1 – 0,1) = 0,54.

Zusätzliche Ressourcen

In den folgenden Artikeln erfahren Sie, wie Sie mit der Binomialverteilung in verschiedenen statistischen Softwareprogrammen arbeiten:

• So berechnen Sie Binomialwahrscheinlichkeiten in Excel
• Wie man Binomialwahrscheinlichkeiten in R berechnet