So führen Sie einen Wilcoxon-Vorzeichen-Rang-Test in R durch

Der Wilcoxon-Vorzeichen-Rang-Test ist die nicht parametrische Version des gepaarten t-Tests. Es wird verwendet, um zu testen, ob es einen signifikanten Unterschied zwischen zwei Populationsmitteln gibt oder nicht, wenn die Verteilung der Unterschiede zwischen den beiden Stichproben nicht als normal angenommen werden kann.

In diesem Tutorial wird erklärt, wie ein Wilcoxon-Vorzeichen-Rang-Test in R durchgeführt wird.

Beispiel: Wilcoxon-Vorzeichen-Rang-Test in R

Angenommen, ein Basketballtrainer möchte wissen, ob ein bestimmtes Trainingsprogramm die Anzahl der Freiwürfe seiner Spieler erhöht. Um dies zu testen, lassen 15 Spieler vor und nach dem Trainingsprogramm jeweils 20 Freiwürfe schießen.

Da jeder Spieler mit sich selbst „gepaart“ werden kann, hatte der Trainer geplant, einen gepaarten t-Test zu verwenden, um festzustellen, ob es einen signifikanten Unterschied zwischen der mittleren Anzahl von Freiwürfen vor und nach dem Trainingsprogramm gibt. Die Verteilung der Unterschiede stellt sich jedoch als nicht normal heraus, sodass der Trainer stattdessen einen Wilcoxon-Vorzeichen-Rang-Test verwendet.

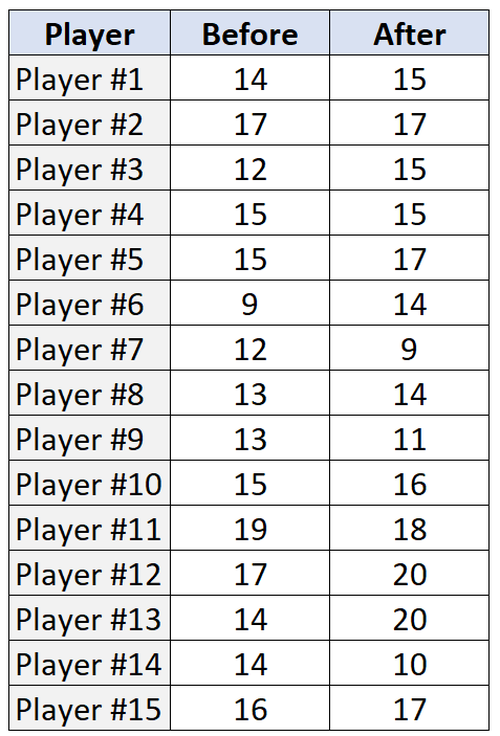
Die folgende Tabelle zeigt die Anzahl der Freiwürfe (aus 20 Versuchen), die jeder der 15 Spieler vor und nach dem Trainingsprogramm ausgeführt hat:

Um den Wilcoxon-Vorzeichen-Rang-Test für diese Daten in R durchzuführen, können wir die Funktion wilcox.test() verwenden, die die folgende Syntax verwendet:

wilcox.test(x, y, paired=TRUE)

wobei:

• x, y: zwei Vektoren von Datenwerten
• paired: Wenn Sie dies auf TRUE setzen, wird R mitgeteilt, dass unsere beiden Vektoren gepaarte Daten enthielten

Der folgende Code veranschaulicht die Verwendung dieser Funktion zur Durchführung des Wilcoxon-Vorzeichen-Rang-Tests für diese Daten:

#Erstellen Sie die beiden Datenvektoren
before <- c (14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c (15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#Wilcoxon-Vorzeichen-Rang-Test durchführen
wilcox.test(before, after, paired=TRUE)

    Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

Die Teststatistik beträgt 29,5 und der entsprechende p-Wert beträgt 0,275. Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Es gibt keinen statistisch signifikanten Unterschied in der Anzahl der Freiwürfe vor und nach der Teilnahme der Spieler am Trainingsprogramm.

Standardmäßig führt diese Funktion einen zweiseitigen Wilcoxon-Signed-Rank-Test durch. Sie können jedoch einen Test für den linken oder einen rechten Test angeben, indem Sie das alternative Argument verwenden:

#Führen Sie den linksseitigen Wilcoxon-Vorzeichen-Rang-Test
wilcox.test(before, after, paired=TRUE, alternative="less")

    Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#Führen Sie den rechtsseitigen Wilcoxon-Vorzeichen-Rang-Test durch
wilcox.test(before, after, paired=TRUE, alternative="greater")

    Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Zusätzliche Ressourcen

Eine Einführung in den Wilcoxon-Vorzeichen-Rang-Test
Wilcoxon Signed-Rank-Tabelle
So führen Sie einen Wilcoxon-Vorzeichen-Rang-Test in Stata durch
So führen Sie einen Wilcoxon-Vorzeichen-Rang-Test in Python durch