So führen Sie den Wilcoxon-Vorzeichen-Rang-Test durch

Der Wilcoxon-Vorzeichen-Rang-Test ist die nicht parametrische Version des gepaarten t-Tests. Es wird verwendet, um zu testen, ob zwischen zwei Populationsmitteln ein signifikanter Unterschied besteht oder nicht.

Wann ist der Wilcoxon-Vorzeichen-Rang-Test anzuwenden?

Verwenden Sie den Wilcoxon-Vorzeichen-Rang-Test, wenn Sie den gepaarten t-Test verwenden möchten, die Verteilung der Unterschiede zwischen den Paaren jedoch stark nicht normal verteilt ist.

Der einfachste Weg, um festzustellen, ob die Unterschiede nicht normal verteilt sind, besteht darin, ein Histogramm der Unterschiede zu erstellen und festzustellen, ob sie einer etwas normalen, „glockenförmigen“ Verteilung folgen.

Beachten Sie, dass der gepaarte t-Test gegenüber Abweichungen von der Normalität ziemlich robust ist. Daher muss die Abweichung von einer Normalverteilung ziemlich stark sein, um die Verwendung des Wilcoxon-Vorzeichen-Rang-Test zu rechtfertigen.

So führen Sie den Wilcoxon-Vorzeichen-Rang-Test durch

Das folgende Beispiel zeigt, wie der Wilcoxon-Vorzeichen-Rang-Test durchgeführt wird.

Ein Basketballtrainer möchte wissen, ob ein bestimmtes Trainingsprogramm die Anzahl der Freiwürfe seiner Spieler erhöht. Um dies zu testen, lassen 15 Spieler vor und nach dem Trainingsprogramm jeweils 20 Freiwürfe schießen.

Da jeder Spieler mit sich selbst „gepaart“ werden kann, hatte der Trainer geplant, einen gepaarten T-Test zu verwenden, um festzustellen, ob es einen signifikanten Unterschied zwischen der mittleren Anzahl von Freiwürfen vor und nach dem Trainingsprogramm gibt.

Die Verteilung der Unterschiede stellt sich jedoch als nicht normal heraus, sodass der Trainer stattdessen den Wilcoxon-Vorzeichen-Rang-Test verwendet.

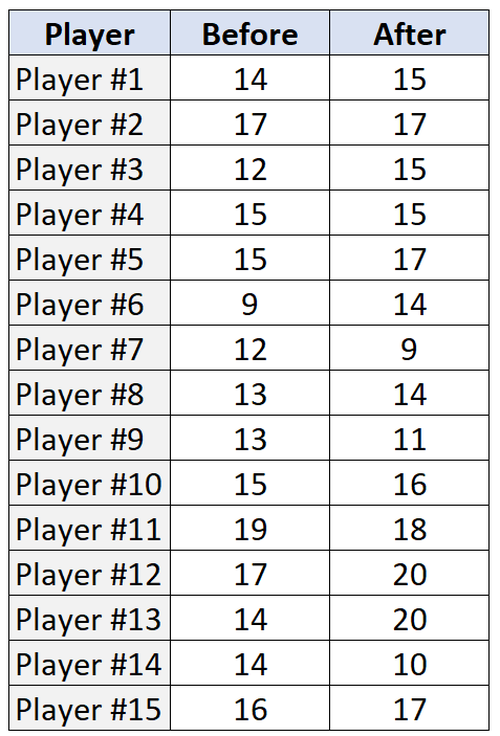
Die folgende Tabelle zeigt die Anzahl der Freiwürfe (aus 20 Versuchen), die jeder der 15 Spieler vor und nach dem Trainingsprogramm ausgeführt hat:

Schritt 1: Geben Sie die Nullhypothese und die Alternativhypothese an.

H ₀: Die mittlere Differenz zwischen den beiden Gruppen ist Null.

H _A: Der Medianunterschied ist negativ. (z.B. machen die Spieler weniger Freiwürfe, bevor sie am Trainingsprogramm teilnehmen)

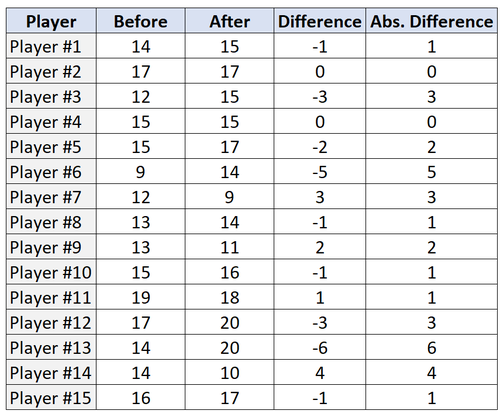
Schritt 2: Finden Sie die Differenz und die absolute Differenz für jedes Paar.

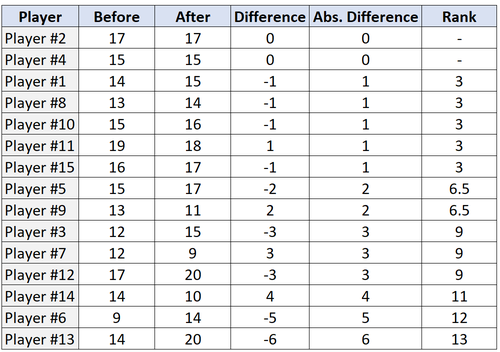
Schritt 3: Ordnen Sie die Paare nach den absoluten Differenzen und weisen Sie einen Rang von den kleinsten zu den größten absoluten Differenzen zu. Ignorieren Sie Paare mit einer absoluten Differenz von „0“ und weisen Sie bei Rängen den Mittelwert der Ränge zu.

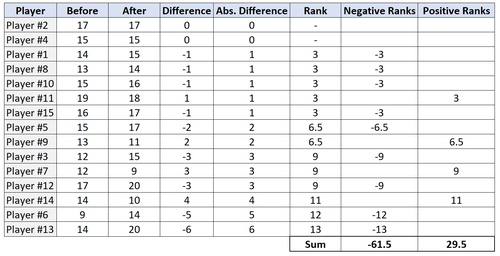
Schritt 4: Finden Sie die Summe der positiven und negativen Ränge.

Schritt 5: Die Nullhypothese ablehnen oder nicht ablehnen.

Die Teststatistik W ist der kleinere der absoluten Werte der positiven und negativen Ränge. In diesem Fall beträgt der kleinere Wert 29,5. Somit ist unsere Teststatistik W = 29,5.

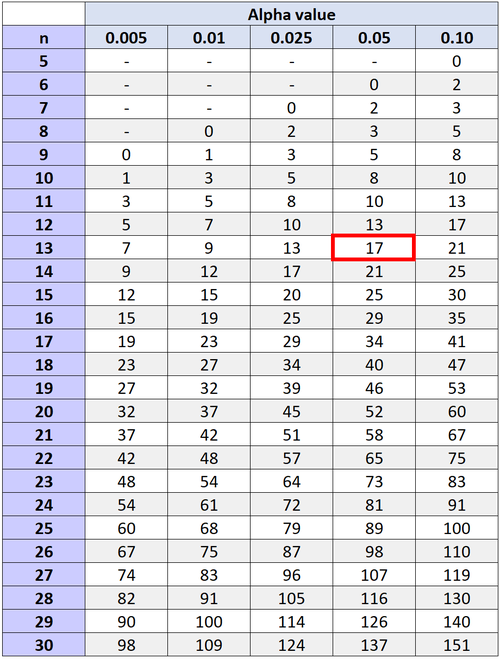
Um zu bestimmen, ob wir die Nullhypothese ablehnen oder nicht ablehnen sollen, können wir auf den kritischen Wert verweisen, der in der Tabelle der kritischen Werte des Wilcoxon-Vorzeichen-Rang-Test gefunden wurde und mit n und unserem gewählten Alpha-Level übereinstimmt.

Wenn unsere Teststatistik W kleiner oder gleich dem kritischen Wert in der Tabelle ist, können wir die Nullhypothese ablehnen. Andernfalls können wir die Nullhypothese nicht ablehnen.

Der kritische Wert, der einem Alpha-Level von 0,05 und n = 13 entspricht (die Gesamtzahl der Paare abzüglich der beiden, für die wir keine Ränge berechnet haben, da sie eine beobachtete Differenz von 0 hatten), beträgt 17.

Da unsere Teststatistik (W = 29,5) nicht kleiner oder gleich 17 ist, können wir die Nullhypothese nicht ablehnen. Wir haben nicht genügend Beweise, um zu sagen, dass das Trainingsprogramm zu einer signifikanten Erhöhung der Anzahl der Freiwürfe der Spieler führt.