Welch-Test: Wann man ihn benutzt + Beispiele

Von Fabian
Kategorie: Tutorials
Tags: Hypothesentest
Lesezeit: 6 Minuten

Wenn wir die Mittelwerte zweier unabhängiger Gruppen vergleichen möchten, können wir zwischen zwei verschiedenen Tests wählen:

Student-t-Test: Bei diesem Test wird davon ausgegangen, dass beide Datengruppen aus Populationen stammen, die einer Normalverteilung folgen, und dass beide Populationen die gleiche Varianz aufweisen.

Welch-Test: Bei diesem Test wird davon ausgegangen, dass beide Datengruppen aus Populationen stammen, die einer Normalverteilung folgen. Es wird jedoch nicht davon ausgegangen, dass diese beiden Populationen dieselbe Varianz aufweisen.

Der Unterschied zwischen dem Student-t-Test und dem Welch-Test

Es gibt zwei Unterschiede bei der Durchführung des Student-t-Tests und des Welch-Tests:

  • Die Teststatistik
  • Die Freiheitsgrade

Students-T-Test:

Teststatistik: ( x 1 – x 2 ) / s p (√ 1 / n 1 + 1 / n 2 )

wobei x 1 und x 2 die Stichprobenmittelwerte sind, n 1 und n 2 die Probengrößen für Probe 1 bzw. Probe 2 sind und wobei s p wie folgt berechnet wird:

s p = √ (n 1 -1) s 12 + (n 2 -1) s 22 / (n 1 + n 2 -2)

wobei s 12 und s 22 die Stichprobenvarianzen sind.

Freiheitsgrade: n 1 + n 2 – 2

Welch-Test

Teststatistik: ( x 1 – x 2 ) / (√ s 12 / n 1 + s 22 / n 2 )

Freiheitsgrade: (s 12 / n 1 + s 22 / n 2 ) 2 / {[(s 12 / n 1 ) 2 / (n 1 – 1)] + [(s 22 / n 2 ) 2 / (n 2 – 1)]}

Die Formel zur Berechnung der Freiheitsgrade für den Welch-Test berücksichtigt die Differenz zwischen den beiden Standardabweichungen. Wenn die beiden Stichproben jedoch die gleichen Standardabweichungen aufweisen, entsprechen die Freiheitsgrade für den Welch-Test genau den Freiheitsgraden für den Student-t-Test.

Typischerweise sind die Standardabweichungen für die beiden Stichproben nicht gleich und daher sind die Freiheitsgrade für den Welch-Test tendenziell kleiner als die Freiheitsgrade für den Student-t-Test.

Es ist auch wichtig zu beachten, dass die Freiheitsgrade für den Welch-Test normalerweise keine ganze Zahl sind. Wenn Sie den Test von Hand durchführen, empfiehlt es sich, auf die nächstniedrigere ganze Zahl abzurunden. Wenn Sie eine Statistiksoftware wie R verwenden, kann die Software den Dezimalwert für die Freiheitsgrade übergeben.

Wann sollten Sie den Welch-Test verwenden?

Einige Leute argumentieren, dass der Welch-Test die Standardauswahl für den Vergleich der Mittelwerte zweier unabhängiger Gruppen sein sollte, da er besser abschneidet als der Student-t-Test, wenn Stichprobengrößen und -abweichungen zwischen den Gruppen ungleich sind, und bei Stichprobengrößen identische Ergebnisse liefert sind Varianzen gleich.

In der Praxis ist es beim Vergleich der Mittelwerte zweier Gruppen unwahrscheinlich, dass die Standardabweichungen für jede Gruppe identisch sind. Daher ist es eine gute Idee, immer den Welch-Test zu verwenden, damit Sie keine Annahmen über gleiche Varianzen treffen müssen.

Beispiele für die Verwendung des Welch-Tests

Als nächstes werden wir den Welch-Test an den folgenden zwei Proben durchführen, um festzustellen, ob sich die Populationsmittelwerte bei einem Signifikanzniveau von 0,05 signifikant unterscheiden:

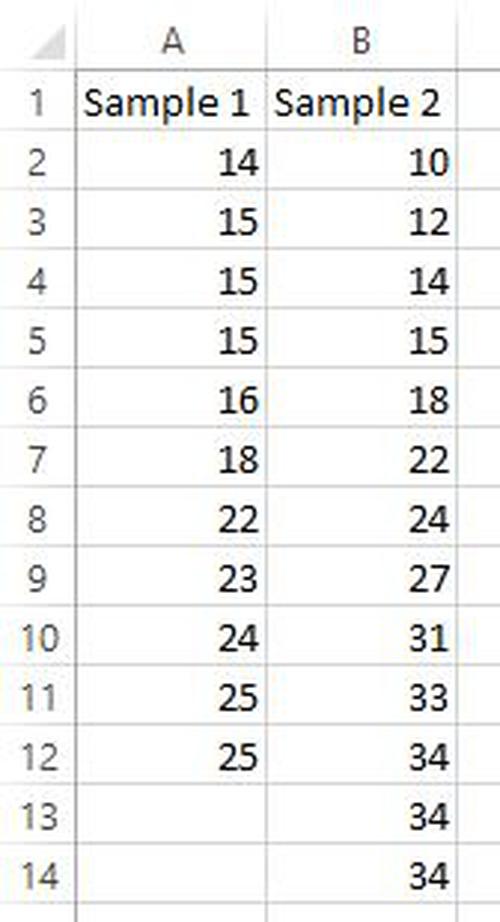
Probe 1: 14, 15, 15, 15, 16, 18, 22, 23, 24, 25, 25

Probe 2: 10, 12, 14, 15, 18, 22, 24, 27, 31, 33, 34, 34, 34

Wir werden veranschaulichen, wie der Test auf drei verschiedene Arten durchgeführt wird:

  • Von Hand
  • Verwenden von Microsoft Excel
  • Verwendung der statistischen Programmiersprache R.

Welch-Test von Hand

Um den Welch-Test von Hand durchzuführen, müssen wir zuerst die Stichprobenmittel, Stichprobenvarianzen und Stichprobengrößen ermitteln:

x 1 – 19,27
x 2 – 23,69
s 12 – 20,42
s 22 – 83,23
n 1 – 11 n 2 – 13

Als nächstes können wir diese Zahlen eingeben, um die Teststatistik zu finden:

Teststatistik: ( x 1 – x 2 ) / (√ s 12 / n 1 + s 22 / n 2 )

Teststatistik: (19,27 – 23,69) / (√ 20,42 / 11 + 83,23 / 13 ) = -4,42 / 2,873 = -1,538

Freiheitsgrade: (s 12 / n 1 + s 22 / n 2 ) 2 / {[(s 12 / n 1 ) 2 / (n 1 – 1)] + [(s 22 / n 2 ) 2 / (n 2 – 1)]}

Freiheitsgrade: (20,42 / 11 + 83,23 / 13) 2 / {[(20,42 / 11) 2 / (11-1)] + [(83,23 / 13) 2 / (13-1)]} = 18,137. Wir runden dies auf die nächstgelegene ganze Zahl von 18 ab.

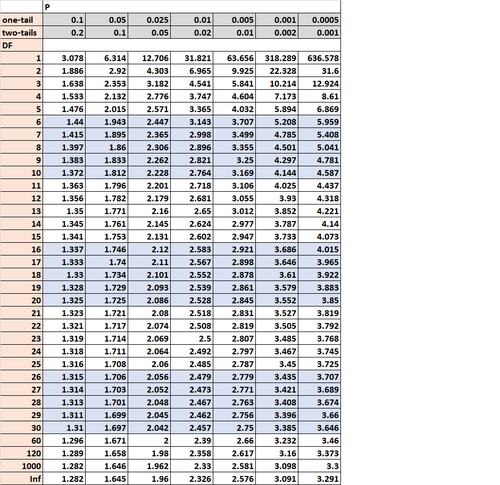
Zuletzt finden wir den t- kritischen Wert in der t-Verteilungstabelle, der einem zweiseitigen Test mit Alpha = 0,05 für 18 Freiheitsgrade entspricht:

T Verteilungstabelle

Der t-kritische Wert beträgt 2,101. Da der absolute Wert unserer Teststatistik (1,538) nicht größer als der kritische Wert t ist, können wir die Nullhypothese des Tests nicht ablehnen. Es gibt nicht genügend Beweise dafür, dass die Mittelwerte der beiden Populationen signifikant unterschiedlich sind.

Welch-Test mit Excel

Um den Welch-Test in Excel durchzuführen, müssen wir zuerst das kostenlose Analysis ToolPak herunterladen. Wenn Sie dies noch nicht in Excel heruntergeladen haben, finden Sie hier ein kurzes Tutorial dazu.

Nachdem Sie das Analysis ToolPak heruntergeladen haben, können Sie die folgenden Schritte ausführen, um den Welch-Test für unsere beiden Beispiele durchzuführen:

1. Geben Sie die Daten ein. Geben Sie die Datenwerte für die beiden Stichproben in die Spalten A und B zusammen mit den Überschriften Stichprobe 1 und Stichprobe 2 in die erste Zelle jeder Spalte ein.

Beispieldaten in Excel

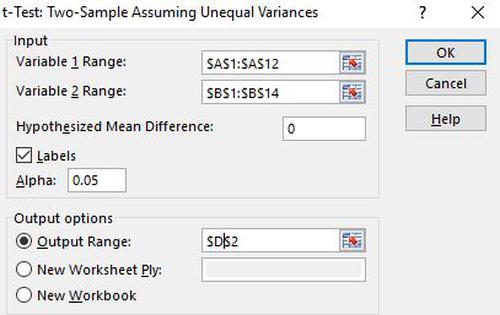
2. Führen Sie den Welch-Test mit dem Analysis ToolPak durch. Navigieren Sie zur Registerkarte Daten am oberen Menüband. Klicken Sie dann in der Gruppe Analyse auf das Symbol für das Datenanalyse.

Analyse-ToolPak in Excel

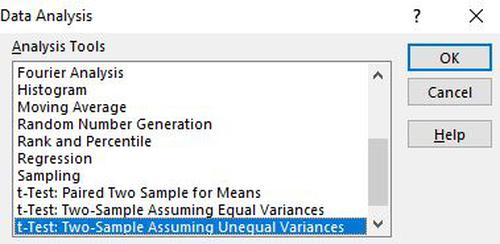
Klicken Sie im daraufhin angezeigten Feld auf t-Test: Two-Sample Assuming Unequal Variances, und klicken Sie dann auf OK.

Welchs T-Test in Excel

Geben Sie zum Schluss die folgenden Werte ein und klicken Sie auf OK:

Welchs T-Test mit Analysis ToolPak in Excel

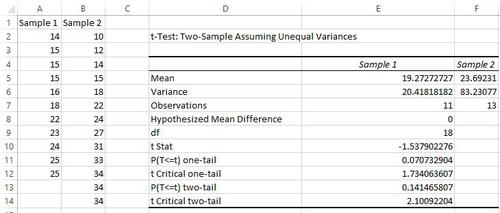
Die folgende Ausgabe sollte erscheinen:

Welchs T-Testergebnisse in Excel

Beachten Sie, dass die Ergebnisse dieses Tests mit den Ergebnissen übereinstimmen, die wir von Hand erhalten haben:

  • t Stat lautet -1,5379.
  • t Critical two-tail beträgt 2.1009.
  • Da der absolute Wert der Teststatistik nicht größer als der kritische zweiseitige Wert ist, unterscheiden sich die Mittelwerte der beiden Populationen statistisch nicht.
  • Außerdem beträgt der zweiseitige p-Wert des Tests (P(T<=t) two-tail) 0,14, was größer als 0,05 ist und bestätigt, dass die beiden Populationsmittelwerte statistisch nicht unterschiedlich sind.

Welch-Test mit R

Der folgende Code zeigt, wie der Welch-Test für unsere beiden Stichproben mit der statistischen Programmiersprache R durchgeführt wird:

#Erstellen Sie zwei Vektoren, um Beispieldatenwerte zu speichern
sample1 <- c (14, 15, 15, 15, 16, 18, 22, 23, 24, 25, 25)
sample2 <- c (10, 12, 14, 15, 18, 22, 24, 27, 31, 33, 34, 34, 34)

#Welch-Test durchführen
t.test(sample1, sample2)

#   Welch Two Sample t-test
#
#data:  sample1 and sample2
#t = -1.5379, df = 18.137, p-value = 0.1413
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -10.453875   1.614714
#sample estimates:
#mean of x mean of y 
# 19.27273  23.69231 
#

Die Funktion t.test() zeigt die folgende relevante Ausgabe an:

  • t: die Teststatistik = -1,5379
  • df: die Freiheitsgrade = 18.137
  • p-Wert: Der p-Wert des zweiseitigen Tests = 0,1413
  • 95%-Konfidenzintervall: Das 95%-Konfidenzintervall für den tatsächlichen Bevölkerungsunterschied bedeutet = (-10,45, 1,61)

Die Ergebnisse dieses Tests stimmen mit den Ergebnissen überein, die wir von Hand und unter Verwendung von Excel erhalten haben: Der Mittelwertunterschied für diese beiden Populationen ist bei alpha = 0,05 statistisch nicht signifikant.

Statistik: Der Weg zur Datenanalyse
Statistik: Der Weg zur Datenanalyse

* Amazon Affiliate Link

Das könnte Sie auch interessieren: