So führen Sie einen t-Test für gepaarte Stichproben in Excel durch

Ein t-Test für gepaarten Proben wird verwendet, um die Mittelwerte von zwei Proben zu vergleichen, wenn jede Beobachtung in einer Probe mit einer Beobachtung in der anderen Probe gepaart werden kann.

In diesem Tutorial wird erklärt, wie ein gepaarter Beispiel-T-Test in Excel durchgeführt wird.

So führen Sie einen t-Test für gepaarte Stichproben in Excel durch

Angenommen, wir möchten wissen, ob ein bestimmtes Studienprogramm die Leistung der Schüler bei einer bestimmten Prüfung erheblich beeinflusst. Um dies zu testen, haben wir 20 Schüler in einer Klasse, die einen Vortest machen. Dann lässt jeder der Studenten zwei Wochen lang am Studienprogramm teilnehmen. Dann wiederholen die Schüler einen Test mit ähnlichen Schwierigkeiten.

Um die Differenz zwischen den Durchschnittswerten beim ersten und zweiten Test zu vergleichen, verwenden wir einen T-Test mit gepaarten Stichproben, da für jeden Schüler die erste Testbewertung mit der zweiten Testbewertung gepaart werden kann.

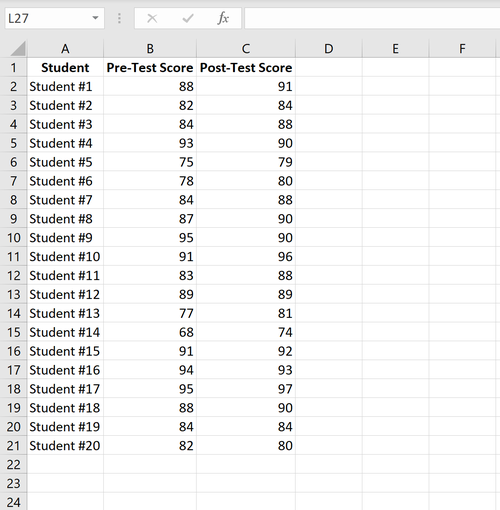
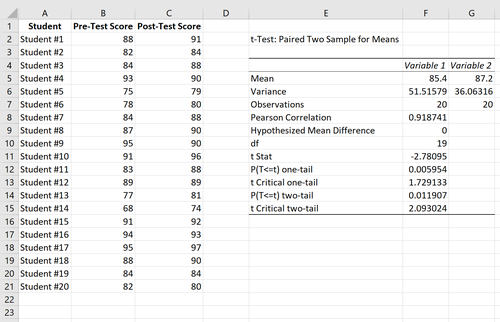
Das folgende Bild zeigt die Ergebnisse vor und nach dem Test für jeden Schüler:

Führen Sie die folgenden Schritte aus, um einen t-Test für gepaarte Stichproben durchzuführen, um festzustellen, ob zwischen dem Vortest und dem Nach-Test ein signifikanter Unterschied in den mittleren Testergebnissen besteht.

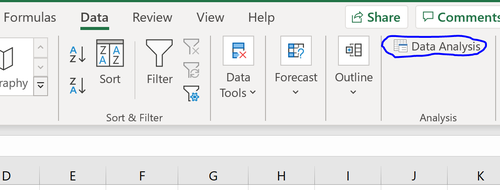
Schritt 1: Öffnen Sie das Data Analysis ToolPak.

Klicken Sie auf der Registerkarte Daten im oberen Menüband auf „Datenanalyse“.

Wenn Sie dies nicht als Option zum Klicken sehen, müssen Sie zuerst das Analyse-ToolPak herunterladen, das völlig kostenlos ist.

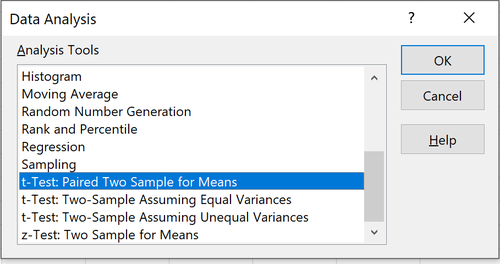
Schritt 2: Wählen Sie den geeigneten Test aus.

Wählen Sie die Option t-Test: gepaarte Stichproben für Mittelwert und klicken Sie dann auf OK.

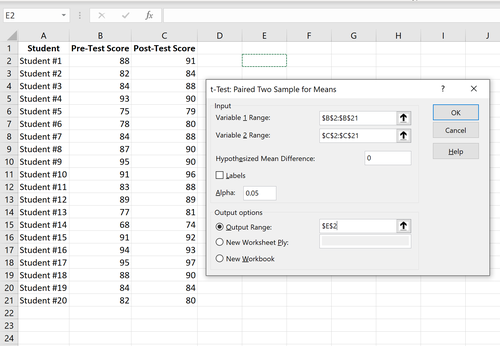
Schritt 3: Geben Sie die erforderlichen Informationen ein.

Geben Sie den Wertebereich für Variable 1 (die Ergebnisse vor dem Test), Variable 2 (die Ergebnisse nach dem Test) und die hypothetische mittlere Differenz ein (in diesem Fall setzen wir „0“, weil wir wissen möchten, ob die wahre mittlere Differenz zwischen den pre-Test und post-Test Ergebnissen 0 sind), und der Ausgabebereich, in dem die Testergebnisse angezeigt werden sollen. Klicken Sie dann auf OK.

Schritt 4: Interpretieren Sie die Ergebnisse.

Sobald Sie im vorherigen Schritt auf OK geklickt haben, werden die Ergebnisse des T-Tests angezeigt.

So interpretieren Sie die Ergebnisse:

Mean: Dies ist der Mittelwert für jede Probe. Die mittlere Punktzahl vor dem Test beträgt 85,4 und die mittlere Punktzahl nach dem Test beträgt 87,2.

Variance: Dies ist die Varianz für jede Stichprobe. Die Varianz der Ergebnisse vor dem Test beträgt 51,51 und die Varianz für die Ergebnisse nach dem Test beträgt 36,06.

Observations: Dies ist die Anzahl der Beobachtungen in jeder Probe. Beide Proben haben 20 Beobachtungen.

Pearson Correlation: Die Korrelation zwischen den Ergebnissen vor und nach dem Test. Es stellt sich heraus, 0,918 zu sein.

Hypothesized mean difference: Die Zahl, die wir „hypothetisieren“, ist der Unterschied zwischen den beiden Mitteln. In diesem Fall haben wir 0 gewählt, weil wir testen möchten, ob es überhaupt einen Unterschied zwischen den Ergebnissen vor und nach dem Test gibt.

df: Die Freiheitsgrade für den t-Test. Dies wird als n-1 berechnet, wobei n die Anzahl der Paare ist. In diesem Fall ist df = 20 – 1 = 19.

t Stat: Die Teststatistik t, die sich als -2,78 herausstellt.

P(T<=t) two-tail: Der p-Wert für einen zweiseitigen t-Test. In diesem Fall ist p = 0,011907. Dies ist kleiner als Alpha = 0,05, daher lehnen wir die Nullhypothese ab. Wir haben genügend Beweise, um zu sagen, dass es einen statistisch signifikanten Unterschied zwischen dem mittleren Ergebnis vor und nach dem Test gibt.

t Critical two-tail: Dies ist der kritische Wert des Tests, der durch Identifizieren des Werts in der t-Verteilungstabelle ermittelt wird, der einem zweiseitigen t-Test mit Alpha = 0,05 und df = 19 entspricht. Dies ergibt 2,093024. Da der Absolutwert unserer Teststatistik t größer als dieser Wert ist, lehnen wir die Nullhypothese ab. Wir haben genügend Beweise, um zu sagen, dass es einen statistisch signifikanten Unterschied zwischen dem mittleren Ergebnis vor und nach dem Test gibt.

Beachten Sie, dass sowohl der p-Wert- als auch der kritische Wertansatz zu derselben Schlussfolgerung führen.

Weiterführende Literatur:

So führen Sie einen Einstichproben-t-Test in Excel durch
So führen Sie einen Zwei-Stichproben-T-Test in Excel durch