Eine einfache Erklärung der statistischen vs. praktischen Signifikanz

Eine statistische Hypothese ist eine Annahme über einen Populationsparameter. Zum Beispiel können wir annehmen, dass die durchschnittliche Körpergröße eines Mannes in einem bestimmten Landkreis 68 Zoll beträgt. Die Annahme über die Körpergröße ist die statistische Hypothese und die wahre durchschnittliche Körpergröße eines Mannes in den USA ist der Bevölkerungsparameter.

Ein Hypothesentest ist ein formaler statistischer Test, den wir verwenden, um eine statistische Hypothese abzulehnen oder nicht abzulehnen. Um einen Hypothesentest durchzuführen, ziehen wir eine Zufallsstichprobe aus der Grundgesamtheit und bestimmen, ob die Stichprobendaten wahrscheinlich aufgetreten sind, vorausgesetzt, die Nullhypothese ist tatsächlich wahr.

Wenn die Stichprobendaten unter dieser Annahme hinreichend unwahrscheinlich sind, können wir die Nullhypothese verwerfen und schlussfolgern, dass ein Effekt existiert.

Die Art und Weise wie wir bestimmen, ob die Stichprobendaten unter der Annahme, dass die Null-Hypothese zutrifft, „hinreichend unwahrscheinlich“ ist, geschieht indem wir ein Signifikanzniveau definieren (normalerweise 0,01, 0,05 oder 0,10) und dann prüfen, ob der p-Wert des Hypothesentests unter diesem Signifikanzniveau liegt.

Wenn der p-Wert kleiner als das Signifikanzniveau ist, sagen wir, dass die Ergebnisse statistisch signifikant sind. Dies bedeutet einfach, dass ein gewisser Effekt existiert, aber es bedeutet nicht unbedingt, dass der Effekt in der realen Welt tatsächlich praktikabel ist. Ergebnisse können statistisch signifikant sein, ohne praktisch signifikant zu sein.

Verwandt: Eine Erklärung von p-Werten und statistischer Signifikanz

Praktische Signifikanz

Hypothesentests können trotz geringer Effektstärke statistisch signifikante Ergebnisse liefern. Es gibt zwei Möglichkeiten, wie kleine Effektstärken kleine (und damit statistisch signifikante) p-Werte erzeugen können:

1. Die Variabilität der Stichprobendaten ist sehr gering. Wenn Ihre Stichprobendaten eine geringe Variabilität aufweisen, kann ein Hypothesentest präzisere Schätzungen des Effekts der Grundgesamtheit liefern, sodass der Test selbst kleine Effekte erkennen kann.

Angenommen, wir möchten einen unabhängigen t-Test bei zwei Stichproben an den folgenden zwei Stichproben durchführen, der die Testergebnisse von 20 Schülern aus zwei verschiedenen Schulen zeigt, um festzustellen, ob sich die durchschnittlichen Testergebnisse zwischen den Schulen signifikant unterscheiden:

Probe 1: 85 85 86 86 85 86 86 86 86 85 85 85 86 85 86 85 86 86 85 86
Probe 2: 87 86 87 86 86 86 86 86 87 86 86 87 86 86 87 87 87 86 87 86

Der Mittelwert für Probe 1 beträgt 85,55 und der Mittelwert für Probe 2 beträgt 86,40. Wenn wir einen unabhängigen t-Test bei zwei Stichproben durchführen, stellt sich heraus, dass die Teststatistik -5,3065 beträgt und der entsprechende p-Wert < 0,0001 ist. Der Unterschied zwischen den Testergebnissen ist statistisch signifikant.

Der Unterschied zwischen den mittleren Testergebnissen dieser beiden Stichproben beträgt nur 0,85, aber die geringe Variabilität der Testergebnisse für jede Schule führt zu einem statistisch signifikanten Ergebnis. Beachten Sie, dass die Standardabweichung für die Scores 0,51 für Probe 1 und 0,50 für Probe 2 beträgt.

Diese geringe Variabilität ermöglichte es dem Hypothesentest, den winzigen Unterschied in den Scores zu erkennen und zu ermöglichen, dass die Unterschiede statistisch signifikant sind.

Der zugrunde liegende Grund dafür, dass eine geringe Variabilität zu statistisch signifikanten Schlussfolgerungen führen kann, liegt darin, dass die Teststatistik t für einen unabhängigen t-Test mit zwei Stichproben wie folgt berechnet wird:

Teststatistik t = [ ( x ₁ – x ₂ ) – d ] / (√ s ² ₁ / n ₁ + s ² ₂ / n ₂ )

wobei s ² ₁ und s ² ₂ die Stichprobenvariation für Stichprobe 1 bzw. Stichprobe 2 angeben. Beachten Sie, dass, wenn diese beiden Zahlen klein sind, der gesamte Nenner der Teststatistik t klein ist.

Und wenn wir durch eine kleine Zahl dividieren, erhalten wir eine große Zahl. Dies bedeutet, dass die Teststatistik t groß und der entsprechende p-Wert klein ist, was zu statistisch signifikanten Ergebnissen führt.

2. Die Stichprobengröße ist sehr groß. Je größer die Stichprobengröße, desto größer ist die statistische Aussagekraft eines Hypothesentests, der es ermöglicht, auch kleine Effekte zu erkennen. Dies kann trotz kleiner Effekte, die möglicherweise keine praktische Signifikanz haben, zu statistisch signifikanten Ergebnissen führen.

Angenommen, wir möchten einen unabhängigen t-Test bei zwei Stichproben an den folgenden zwei Stichproben durchführen, der die Testergebnisse von 20 Schülern aus zwei verschiedenen Schulen zeigt, um festzustellen, ob sich die durchschnittlichen Testergebnisse zwischen den Schulen signifikant unterscheiden:

Probe 1: 88 89 91 94 87 94 94 92 91 86 87 87 92 89 93 90 92 95 89 93
Probe 2: 95 88 93 87 89 90 86 90 95 89 91 92 91 88 94 93 94 87 93 90

Wenn wir für jede Stichprobe ein Boxplot erstellen, um die Verteilung der Punktzahlen anzuzeigen, können wir sehen, dass sie sich sehr ähnlich sehen:

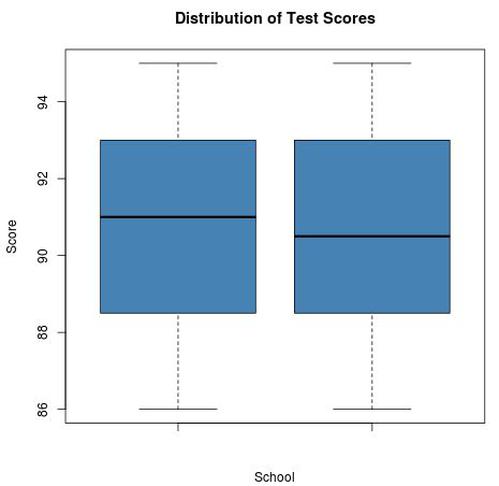
Der Mittelwert für Probe 1 beträgt 90,65 und der Mittelwert für Probe 2 beträgt 90,75. Die Standardabweichung für Probe 1 beträgt 2,77 und die Standardabweichung für Probe 2 beträgt 2,78. Wenn wir einen unabhängigen t-Test bei zwei Stichproben durchführen, stellt sich heraus, dass die Teststatistik -0,113 und der entsprechende p-Wert 0,91 beträgt. Der Unterschied zwischen den mittleren Testergebnissen ist statistisch nicht signifikant.

Überlegen Sie jedoch, ob die Stichprobengrößen der beiden Stichproben beide 200 betragen. In diesem Fall würde ein unabhängiger t-Test bei zwei Stichproben ergeben, dass die Teststatistik -1,97 beträgt und der entsprechende p-Wert knapp unter 0,05 liegt. Der Unterschied zwischen den mittleren Testergebnissen ist statistisch signifikant.

Der Grund dafür, dass große Stichprobengrößen zu statistisch signifikanten Schlussfolgerungen führen können, geht wiederum auf die Teststatistik t für einen zweistichprobenunabhängigen t-Test zurück:

Teststatistik t = [ ( x ₁ – x ₂ ) – d ] / (√ s ² ₁ / n ₁ + s ² ₂ / n ₂ )

Beachten Sie, dass bei _{kleinen n 1} und n ₂ der gesamte Nenner der Teststatistik t klein ist. Und wenn wir durch eine kleine Zahl dividieren, erhalten wir eine große Zahl. Dies bedeutet, dass die Teststatistik t groß und der entsprechende p-Wert klein ist, was zu statistisch signifikanten Ergebnissen führt.

Nutzung von Fachkenntnissen zur Bewertung der praktischen Signifikanz

Um zu bestimmen, ob ein statistisch signifikantes Ergebnis eines Hypothesentests praktisch signifikant ist, ist häufig Fachwissen erforderlich.

In den vorherigen Beispielen, bei denen wir auf Unterschiede zwischen den Testergebnissen für zwei Schulen getestet haben, wäre es hilfreich, das Fachwissen einer Person zu haben, die in Schulen arbeitet oder diese Arten von Tests durchführt, um festzustellen, ob ein mittlerer Unterschied von 1 Punkt hat praktische Implikationen.

Beispielsweise kann eine mittlere Differenz von 1 Punkt bei Alpha = 0,05 statistisch signifikant sein, aber bedeutet dies, dass die Schule mit den niedrigeren Werten den Lehrplan übernehmen sollte, den die Schule mit den höheren Werten verwendet? Oder wäre dies mit zu hohem Verwaltungsaufwand verbunden und wäre die Umsetzung zu teuer/zeitgerecht?

Nur weil es einen statistisch signifikanten Unterschied in den Testergebnissen zwischen zwei Schulen gibt, bedeutet dies nicht, dass die Effektstärke des Unterschieds groß genug ist, um irgendeine Art von Veränderung im Bildungssystem herbeizuführen.

Verwendung von Konfidenzintervallen zur Bewertung der praktischen Signifikanz

Ein weiteres nützliches Werkzeug zur Bestimmung der praktischen Signifikanz ist ein Konfidenzintervall. Ein Konfidenzintervall gibt uns einen Wertebereich an, in den der wahre Populationsparameter wahrscheinlich fallen wird.

Kehren wir zum Beispiel zum Vergleich der Unterschiede in den Testergebnissen zwischen zwei Schulen zurück. Ein Schulleiter kann erklären, dass eine durchschnittliche Punktzahldifferenz von mindestens 5 Punkten erforderlich ist, damit die Schule einen neuen Lehrplan annehmen kann.

In einer Studie können wir feststellen, dass der durchschnittliche Unterschied in den Testergebnissen 8 Punkte beträgt. Das Konfidenzintervall um diesen Mittelwert kann jedoch [4, 12] betragen, was darauf hindeutet, dass 4 die wahre Differenz zwischen den mittleren Testergebnissen sein könnte. In diesem Fall kann der Schulleiter zu dem Schluss kommen, dass die Schule den Lehrplan nicht ändern wird, da das Konfidenzintervall anzeigt, dass die wahre Differenz kleiner als 5 sein könnte.

In einer anderen Studie können wir jedoch feststellen, dass der mittlere Unterschied der Testergebnisse wieder 8 Punkte beträgt, das Konfidenzintervall um den Mittelwert jedoch [6, 10] betragen kann. Da dieses Intervall keine 5 enthält, wird der Schulleiter wahrscheinlich zu dem Schluss kommen, dass der tatsächliche Unterschied in den Testergebnissen größer als 5 ist, und daher feststellen, dass eine Änderung des Lehrplans sinnvoll ist.

Fazit

Abschließend haben wir folgendes gelernt:

• Die statistische Signifikanz zeigt nur an, ob ein Effekt auf einem bestimmten Signifikanzniveau vorliegt.
• Praktische Signifikanz ist, ob dieser Effekt praktische Auswirkungen in der realen Welt hat oder nicht.
• Wir verwenden statistische Analysen zur Ermittlung der statistischen Signifikanz und fachspezifische Expertise zur Einschätzung der praktischen Signifikanz.
• Kleine Effektstärken können zu kleinen p-Werten führen, wenn (1) die Variabilität der Stichprobendaten sehr gering ist und (2) die Stichprobengröße sehr groß ist.
• Indem wir eine minimale Effektstärke definieren, bevor wir einen Hypothesentest durchführen, können wir besser beurteilen, ob das Ergebnis eines Hypothesentests (auch wenn es statistisch signifikant ist) tatsächlich praxistauglich ist.
• Konfidenzintervalle können nützlich sein, um die praktische Signifikanz zu bestimmen. Wenn die minimale Effektstärke nicht innerhalb eines Konfidenzintervalls liegt, können die Ergebnisse praktisch signifikant sein.