So berechnen Sie einen P-Wert aus einem T-Test von Hand

Einer der in der Statistik am häufigsten verwendeten Tests ist der t-Test, mit dem häufig ermittelt wird, ob ein Populationsmittelwert einem bestimmten Wert entspricht.

Angenommen, wir möchten wissen, ob die mittlere Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Um dies zu testen, könnten wir eine Zufallsstichprobe von 20 Pflanzen sammeln, den Stichprobenmittelwert und die Stichprobenstandardabweichung ermitteln und einen t-Test durchführen, um festzustellen, ob die mittlere Höhe tatsächlich 15 Zoll beträgt.

Die Null- und Alternativhypothese für den Test lautet wie folgt:

H ₀: u = 15

H _a: µ ≤ 15

Die Formel für die Teststatistik lautet:

t = ( x – μ) / (s / √ n )

Dabei ist x der Stichprobenmittelwert, μ der hypothetische Mittelwert (in unserem Beispiel 15), s die Standardabweichung der Stichprobe und n die Stichprobengröße.

Sobald wir den Wert von t kennen, können wir eine statistische Software verwenden, um den entsprechenden p-Wert zu finden. Wenn der p-Wert kleiner als ein Alpha-Level ist (übliche Auswahlmöglichkeiten sind .01, .05 und .10), können wir die Nullhypothese ablehnen und daraus schließen, dass die mittlere Höhe der Pflanzen nicht gleich 15 Zoll ist.

Es ist jedoch auch möglich, den p-Wert des Tests von Hand unter Verwendung einer t-Verteilungstabelle zu schätzen. In diesem Beitrag erklären wir, wie das geht.

Beispiel: Berechnung des p-Wertes aus einem t-Test von Hand

Problem: Bob möchte wissen, ob die mittlere Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Um dies zu testen, sammelt er eine Zufallsstichprobe von 20 Pflanzen und stellt fest, dass der Stichprobenmittelwert 14 Zoll und die Standardabweichung der Stichprobe 3 Zoll beträgt. Führen Sie einen T-Test mit einem Alpha-Level von 0.05 durch, um festzustellen, ob die wahre mittlere Körpergröße tatsächlich 15 Zoll beträgt.

Lösung:

Schritt 1: Geben Sie die Nullhypothese und die Alternativhypothese an.

H ₀: u = 15

H _a: µ ≤ 15

Schritt 2: Finden Sie die Teststatistik.

t = ( x – μ) / (s / √ n ) = (14-15) / (3 / √ 20 ) = -1.49

Schritt 3: Finden Sie den p-Wert für die Teststatistik.

Um den p-Wert von Hand zu ermitteln, müssen wir die t-Verteilungstabelle mit n-1 Freiheitsgraden verwenden. In unserem Beispiel beträgt unsere Stichprobengröße n = 20, also n-1 = 19.

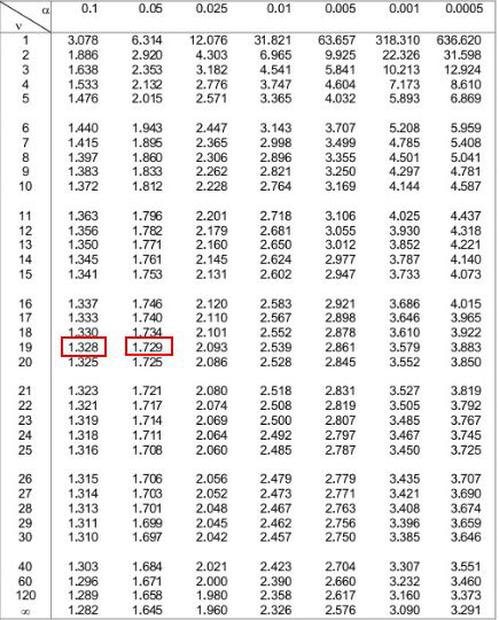
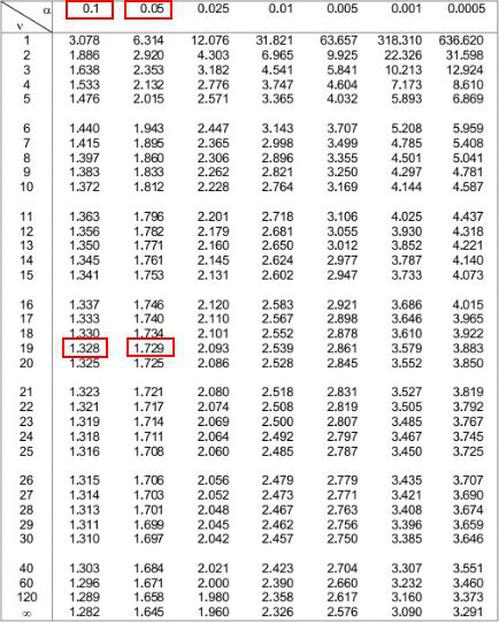
In der folgenden t-Verteilungstabelle müssen wir uns die Zeile ansehen, die auf der linken Seite „19“ entspricht, und versuchen, den absoluten Wert unserer Teststatistik 1.49 zu ermitteln.

Beachten Sie, dass 1.49 nicht in der Tabelle vorkommt, aber es zwischen den beiden Werten 1.328 und 1.729 liegt.

Als nächstes können wir uns die beiden Alpha-Ebenen oben in der Tabelle ansehen, die diesen beiden Zahlen entsprechen. Wir sehen, dass sie 0.1 und 0.5 sind.

Dies bedeutet, dass der p-Wert für einen einseitigen Test zwischen 0.1 und 0.05 liegt. Sagen wir .075. Da unser t-Test zweiseitig ist, müssen wir diesen Wert mit 2 multiplizieren. Unser geschätzter p-Wert beträgt also .,075 * 2 = 0,15.

Schritt 4: Ziehen Sie eine Schlussfolgerung.

Da dieser p-Wert nicht unter unserem gewählten Alpha-Level von 0.05 liegt, können wir die Nullhypothese nicht ablehnen. Daher haben wir nicht genügend Beweise, um zu sagen, dass die wahre mittlere Höhe dieser Pflanzenart anders als 15 Zoll ist.

Überprüfen der Ergebnisse mit einem Taschenrechner

Wir können unsere Teststatistik t und unsere Freiheitsgrade in einen Online-p-Wert-Rechner einstecken, um zu sehen, wie nahe unser geschätzter p-Wert am wahren p-Wert lag:

Der wahre p-Wert beträgt 0.15264, was ziemlich nahe an unserem geschätzten p-Wert von 0.15 liegt.

Fazit

Wir haben in diesem Beitrag gesehen, dass es möglich ist, den p-Wert eines t-Tests mithilfe der t-Verteilungstabelle von Hand zu schätzen. In den meisten Szenarien müssen Sie den p-Wert jedoch nie von Hand berechnen. Stattdessen können Sie entweder statistische Software wie R und Excel oder einen Online-Rechner verwenden, um den genauen p-Wert des Tests zu ermitteln.

In den meisten Fällen, insbesondere bei strengen statistischen Studien und Experimenten, sollten Sie einen Taschenrechner verwenden, um den genauen p-Wert aus einem t-Test zu ermitteln, damit Sie so genau wie möglich sind. Es ist jedoch gut zu wissen, dass Sie dies immer noch können Schätzen Sie den p-Wert aus einem t-Test von Hand, wenn Sie dies unbedingt benötigen.