Ein Mann-Kendall-Trendtest wird verwendet, um festzustellen, ob in Zeitreihendaten ein Trend vorhanden ist oder nicht. Es ist ein nichtparametrischer Test, was bedeutet, dass keine zugrunde liegende Annahme über die Normalität …
Ein Mann-Whitney-U-Test (manchmal auch als Wilcoxon-Rang-Summen-Test bezeichnet) wird verwendet, um die Unterschiede zwischen zwei unabhängigen Proben zu vergleichen, wenn die Probenverteilungen nicht normal verteilt sind und die Probengrößen klein sind (n <30). Es wird als nichtparametrisches Äquivalent zum unabhängigen t-Test mit zwei Stichproben angesehen.
Hier einige Beispiele, wann Sie einen Mann-Whitney-U-Test verwenden könnten:
- Sie möchten die Gehälter von fünf Absolventen der Universität A mit den Gehältern von fünf Absolventen der Universität B vergleichen. Die Gehälter sind nicht normal verteilt.
- Sie möchten wissen, ob der Gewichtsverlust für zwei Gruppen unterschiedlich ist: 12 Personen, die Diät A anwenden, und 10 Personen, die Diät B anwenden. Der Gewichtsverlust ist nicht normal verteilt.
- Sie möchten wissen, ob sich die Punktzahlen von 8 Schülern in Klasse A von denen von 7 Schülern in Klasse B unterscheiden. Die Punktzahlen sind nicht normal verteilt.
In jedem Beispiel haben Sie zwei Gruppen, die Sie vergleichen möchten, die Stichprobenverteilungen sind nicht normal und die Stichprobengrößen sind klein. Daher ist ein Mann-Whitney-U-Test angemessen, solange die folgenden Annahmen erfüllt sind.
Annahmen des Mann-Whitney-U-Tests
Bevor Sie einen Mann-Whitney-U-Test durchführen, müssen Sie sicherstellen, dass die folgenden vier Annahmen erfüllt sind:
- Ordinal oder stetig: Die Variable, die Sie analysieren, ist ordinal oder stetig. Beispiele für Ordnungsvariablen sind Likert-Elemente (z. B. eine 5-Punkte-Skala von „trifft überhaupt nicht zu“ bis „trifft voll zu“). Beispiele für kontinuierliche Variablen sind Größe (gemessen in Zoll), Gewicht (gemessen in Pfund) oder Prüfungsergebnisse (gemessen von 0 bis 100).
- Unabhängigkeit: Alle Beobachtungen beider Gruppen sind unabhängig voneinander.
- Form: Die Formen der Verteilungen für die beiden Gruppen sind ungefähr gleich.
Wenn diese Annahmen erfüllt sind, können Sie einen Mann-Whitney-U-Test durchführen.
So führen Sie einen Mann-Whitney-U-Test durch
Um einen Mann-Whitney-U-Test durchzuführen, folgen wir dem Standardverfahren zum Testen von Hypothesen in fünf Schritten:
1. Geben Sie die Hypothesen an.
In den meisten Fällen wird ein Mann-Whitney-U-Test als zweiseitiger Test durchgeführt. Die Nullhypothese und die Alternativhypothese lauten wie folgt:
H 0: Die beiden Populationen sind gleich
H a: Die beiden Populationen sind nicht gleich
2. Bestimmen Sie ein Signifikanzniveau, das für die Hypothese verwendet werden soll.
Entscheiden Sie sich für ein Signifikanzniveau. Übliche Optionen sind .01, .05 und .1.
3. Finden Sie die Teststatistik.
Die Teststatistik wird als U bezeichnet und ist die kleinere von U 1 und U 2 , wie nachstehend definiert:
U 1 = n 1 n 2 + n 1 (n 1 + 1 ) / 2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 + 1) / 2 – R 2
wobei n 1 und n 2 die Stichprobengrößen für Stichprobe 1 bzw. 2 sind und R 1 und R 2 die Summe der Ränge für Stichprobe 1 bzw. 2 sind.
Die folgenden Beispiele zeigen, wie Sie diese Teststatistik im Detail finden.
4. Die Nullhypothese ablehnen oder nicht ablehnen.
Bestimmen Sie anhand der Teststatistik, ob Sie die Nullhypothese basierend auf dem Signifikanzniveau und dem kritischen Wert in der Mann-Whitney-U-Tabelle ablehnen können oder nicht.
5. Interpretieren Sie die Ergebnisse.
Interpretieren Sie die Testergebnisse im Kontext der gestellten Frage.
Beispiele für die Durchführung eines Mann-Whitney-U-Tests
Die folgenden Beispiele zeigen, wie ein Mann-Whitney-U-Test durchgeführt wird.
Beispiel 1
Wir wollen wissen, ob ein neues Medikament Panikattacken wirksam vorbeugt oder nicht. Insgesamt 12 Patienten werden zufällig in zwei 6er-Gruppen aufgeteilt und erhalten das neue Medikament oder das Placebo. Die Patienten zeichnen dann auf, wie viele Panikattacken sie im Laufe eines Monats haben.
Die Ergebnisse sind unten gezeigt:
| NEUE DROGE | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Führen Sie einen Mann-Whitney-U-Test durch, um festzustellen, ob sich die Anzahl der Panikattacken bei den Patienten in der Placebogruppe im Vergleich zur neuen Arzneimittelgruppe unterscheidet. Verwenden Sie ein Signifikanzniveau von 0,05.
1. Geben Sie die Hypothesen an.
H 0: Die beiden Populationen sind gleich
H a: Die beiden Populationen sind nicht gleich
2. Bestimmen Sie ein Signifikanzniveau, das für die Hypothese verwendet werden soll.
Das Problem sagt uns, dass wir ein .05-Signifikanzniveau verwenden sollen.
3. Finden Sie die Teststatistik.
Denken Sie daran, dass die Teststatistik als U bezeichnet wird und die kleinere von U 1 und U 2 ist , wie unten definiert:
U 1 = n 1 n 2 + n 1 (n 1 + 1 ) / 2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 + 1) / 2 – R 2
wobei n 1 und n 2 die Stichprobengrößen für Stichprobe 1 bzw. 2 sind und R 1 und R 2 die Summe der Ränge für Stichprobe 1 bzw. 2 sind.
Um R 1 und R 2 zu finden , müssen wir die Beobachtungen beider Gruppen kombinieren und sie in der Reihenfolge vom kleinsten zum größten ordnen:
| NEUE DROGE | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Gesamtprobe: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Ränge: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = Summe der Ränge für Probe 1 = 1,5 + 4,5 + 4,5 + 6,5 + 8,5 + 8,5 = 34
R 2 = Summe der Ränge für Probe 2 = 1,5 + 3 + 6,5 + 10 + 11 + 12 = 44
Als nächstes verwenden wir unsere Stichprobengrößen n 1 und n 2 zusammen mit unserer Summe der Ränge R 1 und R 2 , um U 1 und U 2 zu finden.
U 1 = 6 (6) + 6 (6 + 1) / 2 – 34 = 23
U 2 = 6 (6) + 6 (6 + 1) / 2 – 44 = 13
Unsere Teststatistik ist die kleinere von U 1 und U 2 , die zufällig U = 13 ist.
4. Die Nullhypothese ablehnen oder nicht ablehnen.
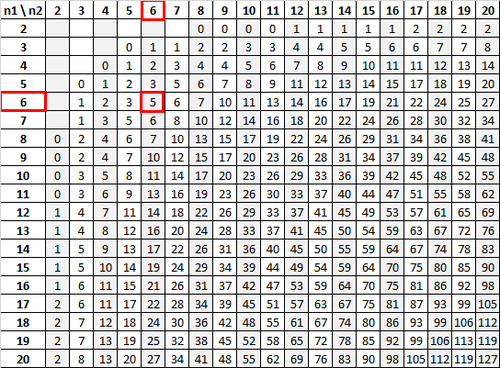
Unter Verwendung von n 1 = 6 und n 2 = 6 mit einem Signifikanzniveau von 0,05 zeigt die Mann-Whitney-U-Tabelle, dass der kritische Wert 5 ist:
Da unsere Teststatistik (13) größer als unser kritischer Wert (5) ist, können wir die Nullhypothese nicht ablehnen.
5. Interpretieren Sie die Ergebnisse.
Da wir die Nullhypothese nicht zurückweisen konnten, gibt es keine ausreichenden Beweise dafür, dass sich die Anzahl der Panikattacken bei Patienten in der Placebogruppe von der neuen Arzneimittelgruppe unterscheidet.
Beispiel 2
Wir möchten wissen, ob eine Woche lang 30 Minuten pro Tag lernen oder nicht, damit die Schüler bei einem Test besser abschneiden können. Insgesamt 15 Patienten werden zufällig einer Studie oder einer Gruppe ohne Studie zugeordnet. Nach einer Woche machen alle Schüler den gleichen Test.
Die Testergebnisse für die beiden Gruppen sind nachstehend aufgeführt:
| STUDIE | KEINE STUDIE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Führen Sie einen Mann-Whitney-U-Test durch, um festzustellen, ob es einen Unterschied zwischen den Testergebnissen für die Studie und der Gruppe ohne Studie gibt. Verwenden Sie ein Signifikanzniveau von 0,01.
1. Geben Sie die Hypothesen an.
H 0: Die beiden Populationen sind gleich
H a: Die beiden Populationen sind nicht gleich
2. Bestimmen Sie ein Signifikanzniveau, das für die Hypothese verwendet werden soll.
Das Problem sagt uns, dass wir ein Signifikanzniveau von 0,01 verwenden sollen.
3. Finden Sie die Teststatistik.
Denken Sie daran, dass die Teststatistik als U bezeichnet wird und die kleinere von U 1 und U 2 ist , wie unten definiert:
U 1 = n 1 n 2 + n 1 (n 1 + 1 ) / 2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 + 1) / 2 – R 2
wobei n 1 und n 2 die Stichprobengrößen für Stichprobe 1 bzw. 2 sind und R 1 und R 2 die Summe der Ränge für Stichprobe 1 bzw. 2 sind.
Um R 1 und R 2 zu finden , müssen wir die Beobachtungen beider Gruppen kombinieren und sie in der Reihenfolge vom kleinsten zum größten ordnen:
| STUDIE | KEINE STUDIE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Gesamtprobe: 72 , 75 , 80 , 81 , 84 , 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Ränge: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = Summe der Ränge für Probe 1 = 5 + 7 + 8 + 9 + 10 + 12 + 14 + 15 = 80
R 2 = Summe der Ränge für Probe 2 = 1 + 2 + 3 + 4 + 6 + 11 + 13 = 40
Als nächstes verwenden wir unsere Stichprobengrößen n 1 und n 2 zusammen mit unserer Summe der Ränge R 1 und R 2 , um U 1 und U 2 zu finden.
U 1 = 8 (7) + 8 (8 + 1) / 2 – 80 = 12
U 2 = 8 (7) + 7 (7 + 1) / 2 – 40 = 44
Unsere Teststatistik ist die kleinere von U 1 und U 2 , die zufällig U = 12 ist.
4. Die Nullhypothese ablehnen oder nicht ablehnen.
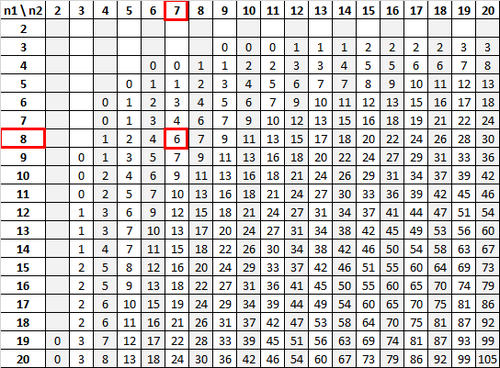
Unter Verwendung von n 1 = 8 und n 2 = 7 mit einem Signifikanzniveau von 0,01 zeigt die Mann-Whitney-U-Tabelle, dass der kritische Wert 6 ist:
Da unsere Teststatistik (12) größer als unser kritischer Wert (6) ist, können wir die Nullhypothese nicht ablehnen.
5. Interpretieren Sie die Ergebnisse.
Da wir die Nullhypothese nicht zurückgewiesen haben, gibt es keine ausreichenden Beweise dafür, dass sich die Testergebnisse der Studierenden, die studiert haben, von den Testergebnissen der Studierenden unterscheiden, die nicht studiert haben.
Zusätzliche Ressourcen
Mann-Whitney U-Tabelle
So führen Sie einen Mann-Whitney-U-Test in R durch
So führen Sie einen Mann-Whitney-U-Test in Python durch
So führen Sie einen Mann-Whitney-U-Test in SPSS durch
So führen Sie einen Mann-Whitney-U-Test in Stata durch
So führen Sie einen Mann-Kendall-Trendtest in Python durch
So führen Sie einen Chow-Test in Python durch
Ein Chow-Test wird verwendet, um zu testen, ob die Koeffizienten in zwei verschiedenen Regressionsmodellen auf verschiedenen Datensätzen gleich sind.
Dieser Test wird typischerweise im Bereich der Ökonometrie mit Zeitreihendaten verwendet …