Einführung in die Lasso-Regression

Bei der gewöhnlichen multiplen linearen Regression verwenden wir einen Satz von p Prädiktorvariablen und eine Antwortvariable, um ein Modell der Form anzupassen:

Y = β ₀ + β ₁ X ₁ + β ₂ X ₂ +… + β _p X _p + ε

wo:

• Y: Die Antwortvariable
• X _j: Die j-te Prädiktorvariable
• β _j: Der durchschnittliche Effekt einer Zunahme von X _{j um} eine Einheit auf Y, wobei alle anderen Prädiktoren festgehalten werden
• ε: Der Fehlerterm

Die Werte für β ₀ , β ₁ , B ₂ ,…, β _p werden nach der Methode der kleinsten Quadrate ausgewählt, die die Summe der quadratischen Residuen (RSS) minimiert:

RSS = Σ (y _i - ŷ _i ) ²

wo:

• Σ: Ein griechisches Symbol, das Summe bedeutet
• y _i: Der tatsächliche Antwortwert für die i-te Beobachtung
• ŷ _i: Der vorhergesagte Antwortwert basierend auf dem multiplen linearen Regressionsmodell

Wenn die Prädiktorvariablen jedoch stark korreliert sind, kann Multikollinearität zu einem Problem werden. Dies kann dazu führen, dass die Koeffizientenschätzungen des Modells unzuverlässig sind und eine hohe Varianz aufweisen. Das heißt, wenn das Modell auf einen neuen Datensatz angewendet wird, den es zuvor noch nicht gesehen hat, ist die Leistung wahrscheinlich schlecht.

Eine Möglichkeit, dieses Problem zu umgehen, besteht darin, eine als Lasso-Regression bekannte Methode zu verwenden, mit der stattdessen Folgendes minimiert werden soll:

RSS + λΣ | β _j |

wobei j im Bereich von 1 bis p liegt und λ ≥ 0 ist.

Dieser zweite Term in der Gleichung ist als Shrinkage Penalty bekannt.

Wenn λ = 0 ist, hat dieser Strafausdruck keine Auswirkung und die Lasso-Regression erzeugt dieselben Koeffizientenschätzungen wie die kleinsten Quadrate.

Wenn sich λ jedoch der Unendlichkeit nähert, wird die Schrumpfungsstrafe einflussreicher und die Prädiktorvariablen, die im Modell nicht importierbar sind, werden gegen Null geschrumpft und einige werden sogar aus dem Modell entfernt.

Warum Lasso-Regression verwenden?

Der Vorteil der Lasso-Regression gegenüber der Regression der kleinsten Quadrate liegt im Kompromiss zwischen Bias und Varianz.

Denken Sie daran, dass der mittlere quadratische Fehler (MSE) eine Metrik ist, mit der wir die Genauigkeit eines bestimmten Modells messen können. Sie wird wie folgt berechnet:

MSE = Var ( f̂ ( x ₀ )) + [Bias ( f̂ ( x ₀ ))] ² + Var (ε)

MSE = Varianz + Vorspannung ² + nicht reduzierbarer Fehler

Die Grundidee der Lasso-Regression besteht darin, eine kleine Verzerrung einzuführen, damit die Varianz wesentlich verringert werden kann, was zu einer niedrigeren Gesamt-MSE führt.

Betrachten Sie zur Veranschaulichung die folgende Tabelle:

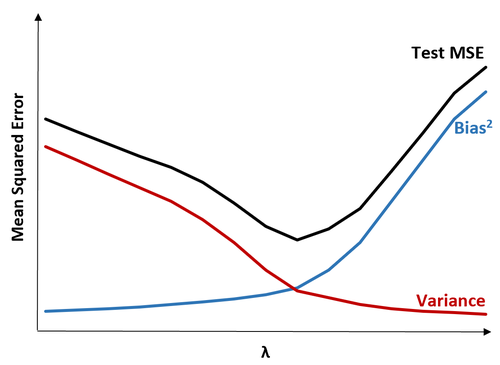
Beachten Sie, dass mit zunehmendem λ die Varianz mit sehr geringer Zunahme der Vorspannung erheblich abnimmt. Ab einem bestimmten Punkt nimmt die Varianz jedoch weniger schnell ab und die Schrumpfung der Koeffizienten führt dazu, dass sie signifikant unterschätzt werden, was zu einem starken Anstieg der Vorspannung führt.

Wir können dem Diagramm entnehmen, dass die Test-MSE am niedrigsten ist, wenn wir einen Wert für λ wählen, der einen optimalen Kompromiss zwischen Bias und Varianz ergibt.

Wenn λ = 0 ist, hat der Strafausdruck bei der Lasso-Regression keine Auswirkung und erzeugt daher die gleichen Koeffizientenschätzungen wie die kleinsten Quadrate. Durch Erhöhen von λ bis zu einem bestimmten Punkt können wir jedoch die Gesamttest-MSE reduzieren.

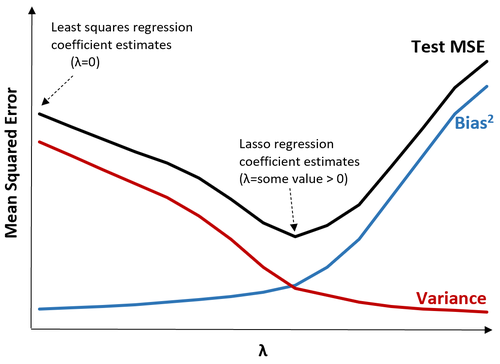
Dies bedeutet, dass die Modellanpassung durch Lasso-Regression kleinere Testfehler erzeugt als die Modellanpassung durch Regression der kleinsten Quadrate.

Lasso-Regression vs. Ridge-Regression

Die Lasso-Regression und die Ridge-Regression werden beide als Regularisierungsmethoden bezeichnet, da beide versuchen, die Summe der quadratischen Residuen (RSS) zusammen mit einem bestimmten Strafzeitraum zu minimieren.

Mit anderen Worten, sie beschränken oder regulieren die Koeffizientenschätzungen des Modells.

Die Strafbegriffe, die sie verwenden, sind jedoch etwas anders:

• Die Lasso-Regression versucht, RSS + λΣ | β _j | zu minimieren
• Die Ridge-Regression versucht, RSS + λΣβ _j ² zu minimieren

Wenn wir die Gratregression verwenden, werden die Koeffizienten jedes Prädiktors gegen Null geschrumpft, aber keiner von ihnen kann vollständig gegen Null gehen.

Umgekehrt ist es bei Verwendung der Lasso-Regression möglich, dass einige der Koeffizienten vollständig auf Null gehen , wenn λ ausreichend groß wird.

In technischer Hinsicht kann die Lasso-Regression „spärliche“ Modelle erzeugen - Modelle, die nur eine Teilmenge der Prädiktorvariablen enthalten.

Dies wirft die Frage auf: Ist die Ridge-Regression oder die Lasso-Regression besser?

Die Antwort: Es kommt darauf an!

In Fällen, in denen nur eine kleine Anzahl von Prädiktorvariablen signifikant ist, ist die Lasso-Regression tendenziell besser, da nicht signifikante Variablen vollständig auf Null verkleinert und aus dem Modell entfernt werden können.

Wenn jedoch viele Prädiktorvariablen im Modell signifikant sind und ihre Koeffizienten ungefähr gleich sind, ist die Ridge-Regression tendenziell besser, da alle Prädiktoren im Modell erhalten bleiben.

Um festzustellen, welches Modell besser Vorhersagen treffen kann, führen wir eine k-fache Kreuzvalidierung durch. Welches Modell den niedrigsten mittleren Testfehler (MSE) erzeugt, ist das bevorzugte Modell.

Schritte zur Durchführung einer Lasso-Regression in der Praxis

Die folgenden Schritte können verwendet werden, um eine Lasso-Regression durchzuführen:

Schritt 1: Berechnen Sie die Korrelationsmatrix und die VIF-Werte für die Prädiktorvariablen.

Zunächst sollten wir eine Korrelationsmatrix erstellen und die VIF-Werte (Varianzinflationsfaktor) für jede Prädiktorvariable berechnen.

Wenn wir eine hohe Korrelation zwischen Prädiktorvariablen und hohen VIF-Werten feststellen (einige Texte definieren einen „hohen“ VIF-Wert als 5, während andere 10 verwenden), ist eine Lasso-Regression wahrscheinlich angemessen.

Wenn jedoch keine Multikollinearität in den Daten vorhanden ist, besteht möglicherweise überhaupt keine Notwendigkeit, eine Lasso-Regression durchzuführen. Stattdessen können wir eine gewöhnliche Regression der kleinsten Quadrate durchführen.

Schritt 2: Passen Sie das Lasso-Regressionsmodell an und wählen Sie einen Wert für λ.

Sobald wir festgestellt haben, dass die Lasso-Regression für die Verwendung geeignet ist, können wir das Modell (unter Verwendung gängiger Programmiersprachen wie R oder Python) unter Verwendung des optimalen Werts für λ anpassen.

Um den optimalen Wert für λ zu bestimmen, können wir mehrere Modelle mit unterschiedlichen Werten für λ anpassen und λ als den Wert auswählen, der die niedrigste Test-MSE erzeugt.

Schritt 3: Vergleichen Sie die Lasso-Regression mit der Ridge-Regression und der gewöhnlichen Regression der kleinsten Quadrate.

Zuletzt können wir unser Lasso-Regressionsmodell mit einem Ridge-Regressionsmodell und einem Regressionsmodell der kleinsten Quadrate vergleichen, um mithilfe der k-fachen Kreuzvalidierung zu bestimmen, welches Modell die niedrigste Test-MSE erzeugt.

Abhängig von der Beziehung zwischen den Prädiktorvariablen und der Antwortvariablen ist es durchaus möglich, dass eines dieser drei Modelle die anderen in verschiedenen Szenarien übertrifft.

Lasso-Regression in R & Python

In den folgenden Tutorials wird erläutert, wie Sie eine Lasso-Regression in R und Python durchführen:

Lasso-Regression in R (Schritt für Schritt)
Lasso-Regression in Python (Schritt für Schritt)