Eine Einführung in Klassifikations- und Regressionsbäume

Wenn die Beziehung zwischen einem Satz von Prädiktorvariablen und einer Antwortvariablen linear ist, können Methoden wie die multiple lineare Regression genaue Vorhersagemodelle erzeugen.

Wenn jedoch die Beziehung zwischen einer Reihe von Prädiktoren und einer Antwort stark nichtlinear und komplex ist, können nichtlineare Methoden eine bessere Leistung erbringen.

Ein solches Beispiel für eine nichtlineare Methode sind Klassifikations- und Regressionsbäume.

Wie der Name schon sagt, verwenden Klassifikations- und Regressionsbaum-Modelle eine Reihe von Prädiktorvariablen, um Entscheidungsbäume zu erstellen, die den Wert einer Antwortvariablen vorhersagen.

Angenommen, wir haben einen Datensatz, der die Prädiktorvariablen Jahre gespielt und durchschnittliche Home Runs zusammen mit der Antwortvariablen Jahresgehalt für Hunderte von professionellen Baseballspielern enthält.

So könnte ein Regressionsbaum für diesen Datensatz aussehen:

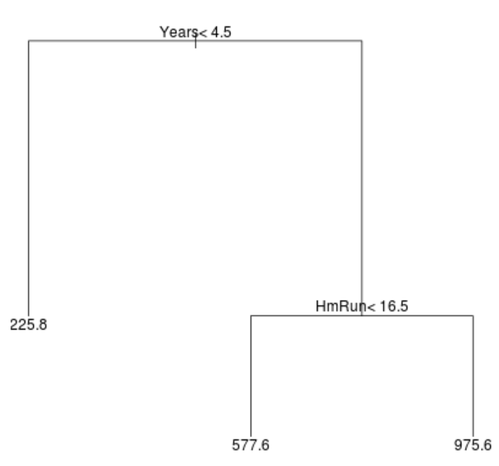
Der Baum wird folgendermaßen interpretiert:

• Spieler mit weniger als 4,5 Jahren haben ein vorhergesagtes Gehalt von 225,8.000 USD.
• Spieler mit mehr als oder gleich 4,5 Jahren und weniger als 16,5 durchschnittlichen Home Runs haben ein vorhergesagtes Gehalt von 577,6.000 USD.
• Spieler mit mehr als oder gleich 4,5 Jahren und mehr als oder gleich 16,5 durchschnittlichen Home Runs haben ein vorhergesagtes Gehalt von 975,6.000 USD. Die Ergebnisse dieses Modells sollten intuitiv sinnvoll sein: Spieler mit mehrjähriger Erfahrung und durchschnittlicheren Home Runs verdienen tendenziell höhere Gehälter.

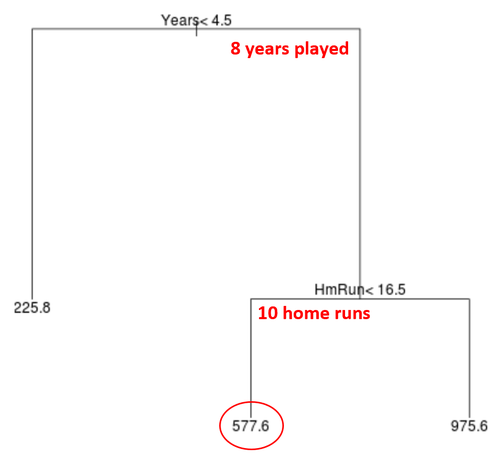
Wir können dieses Modell dann verwenden, um das Gehalt eines neuen Spielers vorherzusagen.

Angenommen, ein bestimmter Spieler hat 8 Jahre gespielt und durchschnittlich 10 Home Runs pro Jahr. Nach unserem Modell würden wir vorhersagen, dass dieser Spieler ein Jahresgehalt von 577,6.000 USD hat.

Ein paar Anmerkungen zum Baum:

• Die erste Prädiktorvariable am oberen Rand des Baums ist die wichtigste, d.hdie einflussreichste für die Vorhersage des Werts der Antwortvariablen. In diesem Fall können die gespielten Jahre das Gehalt besser vorhersagen als die durchschnittlichen Home Runs.
• Die Regionen am unteren Rand des Baums werden als Endknoten bezeichnet. Dieser bestimmte Baum hat drei Endknoten.

Schritte zum Erstellen von Klassifikations- und Regressionsbaum-Modellen

Mit den folgenden Schritten können Sie ein Modell für einen bestimmten Datensatz erstellen:

Schritt 1: Verwenden Sie die rekursive binäre Aufteilung, um einen großen Baum auf den Trainingsdaten zu erstellen.

Zunächst verwenden wir einen gierigen (engl. greedy) Algorithmus, der als rekursive binäre Aufteilung bekannt ist, um einen Regressionsbaum mit der folgenden Methode zu vergrößern:

• Betrachten Sie alle Prädiktorvariablen X ₁ , X ₂ ,…, X _p und alle möglichen Werte der Schnittpunkte für jeden der Prädiktoren, und wählen Sie dann den Prädiktor und den Schnittpunkt so aus, dass der resultierende Baum den niedrigsten RSS-Wert aufweist (verbleibender Standardfehler).
• Für Klassifikationsbäume wählen wir den Prädiktor und den Schnittpunkt so, dass der resultierende Baum die niedrigste Fehlklassifikationsrate aufweist.
• Wiederholen Sie diesen Vorgang und stoppen Sie nur, wenn jeder Endknoten weniger als eine Mindestanzahl von Beobachtungen aufweist.

Dieser Algorithmus ist gierig, weil er bei jedem Schritt des Baumbildungsprozesses die beste Aufteilung ermittelt, die nur auf diesem Schritt basiert, anstatt nach vorne zu schauen und eine Aufteilung auszuwählen, die in einem zukünftigen Schritt zu einem besseren Gesamtbaum führt.

Schritt 2: Wenden Sie eine Kostenkomplexitätsbeschneidung auf den großen Baum an, um eine Folge der besten Bäume als Funktion von α zu erhalten.

Sobald wir den großen Baum gezüchtet haben, müssen wir den Baum mit einer Methode beschneiden, die als Kostenkomplexitätsbeschneidung bezeichnet wird und wie folgt funktioniert:

• Suchen Sie für jeden möglichen Baum mit T-Endknoten den Baum, der RSS + α | T | minimiert.
• Beachten Sie, dass Bäume mit mehr Endknoten bestraft werden, wenn wir den Wert von α erhöhen. Dies stellt sicher, dass der Baum nicht zu komplex wird.

Dieser Prozess führt zu einer Folge der besten Bäume für jeden Wert von α.

Schritt 3: Verwenden Sie die k-fache Kreuzvalidierung, um α zu wählen.

Sobald wir den besten Baum für jeden Wert von α gefunden haben, können wir eine k-fache Kreuzvalidierung anwenden, um den Wert von α zu wählen, der den Testfehler minimiert.

Schritt 4: Wählen Sie das endgültige Modell.

Zuletzt wählen wir das endgültige Modell als dasjenige, das dem gewählten Wert von α entspricht.

Vor- und Nachteile von Klassifikations- und Regressionsbaume-Modellen

Vorteile:

• Sie sind leicht zu interpretieren.
• Sie sind leicht zu erklären.
• Sie sind leicht zu visualisieren.
• Sie können sowohl auf Regressions- als auch auf Klassifikationsprobleme angewendet werden.

Nachteile:

• Sie haben tendenziell nicht so viel Vorhersagegenauigkeit wie andere nichtlineare Algorithmen für maschinelles Lernen. Durch die Zusammenfassung vieler Entscheidungsbäume mit Methoden wie Bagging, Boosting und Random Forests kann jedoch ihre Vorhersagegenauigkeit verbessert werden.

Verwandte Themen:
Anpassen von Klassifikations- und Regressionsbäumen in R