Was sind Dichtekurven? (Erklärung & Beispiele)

Eine Dichtekurve ist eine Kurve in einem Diagramm, die die Verteilung von Werten in einem Datensatz darstellt. Sie ist aus drei Gründen nützlich:

1. Eine Dichtekurve gibt uns eine gute Vorstellung von der "Form" einer Verteilung, einschließlich der Frage, ob eine Verteilung eine oder mehrere "Spitzen" häufig vorkommender Werte aufweist und ob die Verteilung nach links oder rechts verzerrt ist.

2. Anhand einer Dichtekurve lässt sich visuell erkennen, wo sich der Mittelwert und der Median einer Verteilung befinden.

3. Anhand einer Dichtekurve lässt sich visuell erkennen, wie viel Prozent der Beobachtungen in einem Datensatz zwischen verschiedene Werte fallen.

Die bekannteste Dichtekurve ist die glockenförmige Kurve, die die Normalverteilung darstellt.

Um ein besseres Verständnis der Dichtekurven zu erlangen, betrachten Sie das folgende Beispiel.

Beispiel: Erstellen & Interpretieren einer Dichtekurve

Angenommen, wir haben den folgenden Datensatz, der die Höhe von 20 verschiedenen Pflanzen (in Zoll) auf einem bestimmten Feld zeigt:

4, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Wenn wir ein einfaches Histogramm erstellen würden, um die relativen Häufigkeiten der einzelnen Werte anzuzeigen, würde es wie folgt aussehen:

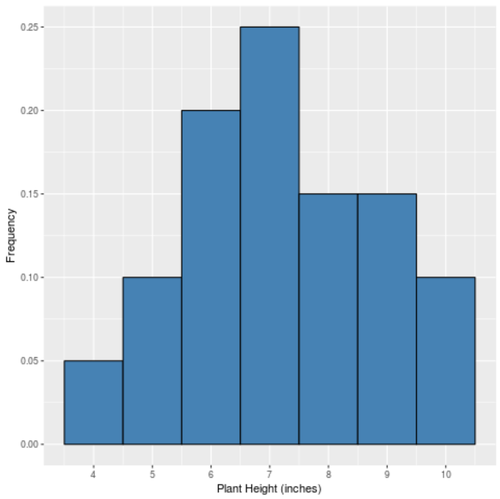
Die x-Achse zeigt den Datenwert und die y-Achse zeigt die relative Häufigkeit (z.B. der Wert "7" kommt 5 Mal von 20 Gesamtwerten im Datensatz vor, hat also eine relative Häufigkeit von 25% oder 0,25.

Und wenn wir eine Dichtekurve erstellen würden, um die "Form" dieser Verteilung zu erfassen, würde sie wie folgt aussehen:

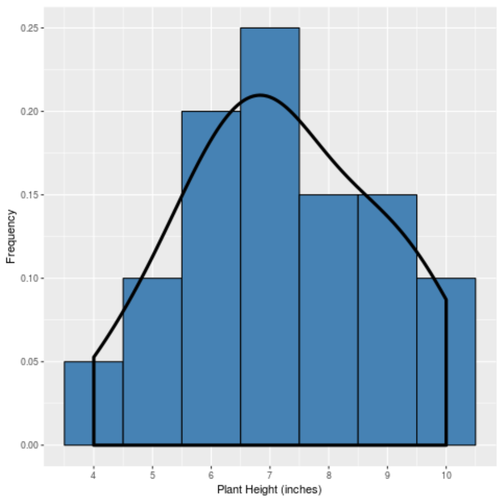
Die Kurve ist in der Mitte der Verteilung am höchsten, weil sich dort die meisten Werte befinden. Sie ist auch in der Nähe der Enden der Verteilung am niedrigsten, weil weniger Pflanzen diese Werte annehmen (z. B. eine Höhe von 4 Zoll oder 10 Zoll).

Wie man Dichtekurven interpretiert

Dichtekurven gibt es in allen Formen und Größen, und sie ermöglichen es uns, ein schnelles visuelles Verständnis der Verteilung von Werten in einem bestimmten Datensatz zu gewinnen. Sie sind insbesondere nützlich, um Folgendes zu visualisieren:

1. Schiefe

Skewness ist eine Methode zur Beschreibung der Symmetrie einer Verteilung. Anhand von Dichtekurven kann man schnell erkennen, ob ein Diagramm linksschief, rechtsschief oder gar nicht schief ist:

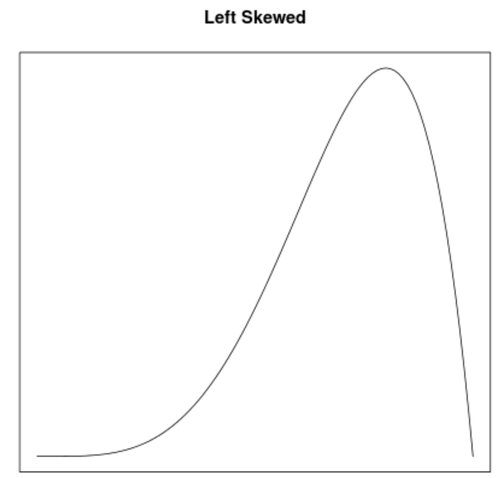
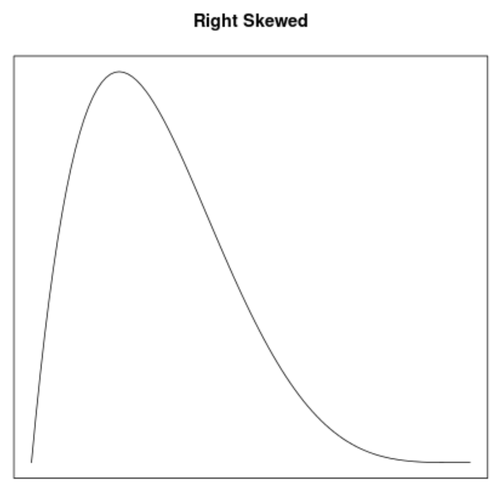
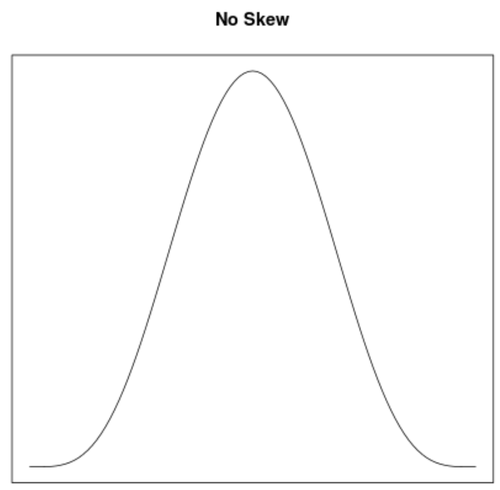
2. die Lage des Mittelwertes & Medians

Abhängig von der Schiefe einer Dichtekurve kann man schnell feststellen, ob der Mittelwert oder der Median in einer bestimmten Verteilung größer ist. Im Einzelnen:

• Wenn eine Dichtekurve linksschief ist, dann ist der Mittelwert weniger als der Median.
• Ist eine Dichtekurve rechtsschief, dann ist der Mittelwert größerals der Median.
• Wenn eine Dichtekurve keine Schiefe hat, dann ist der Mittelwert gleichdem Median.

3. Anzahl der Peaks

Dichtekurven ermöglichen es uns auch, schnell zu erkennen, wie viele "Spitzen" es in einer bestimmten Verteilung gibt. In jedem der obigen Beispiele hatten die Verteilungen nur eine Spitze, daher würden wir diese Verteilungen als unimodal bezeichnen.

Es gibt jedoch auch Verteilungen mit zwei Spitzen, die wir bimodale Verteilungen nennen. Und in seltenen Fällen können wir auch multimodale Verteilungen haben, die zwei oder mehr Spitzen haben.

Indem man einfach eine Dichtekurve für einen bestimmten Datensatz erstellt, kann man schnell sehen, wie viele Spitzen die Verteilung hat.

Eigenschaften von Dichtekurven

Dichtekurven haben die folgenden Eigenschaften:

• Die Fläche unter der Kurve summiert sich immer zu 100%.
• Die Kurve wird nie unter die x-Achse eintauchen.

Behalten Sie diese beiden Fakten im Hinterkopf, wenn Sie Dichtekurven für verschiedene Verteilungen erstellen oder interpretieren.

Zusätzliche Ressourcen

Einführung in die relativen Häufigkeitshistogramme
Erstellung einer Glockenkurve in Excel
Anleitung zur Erstellung einer Glockenkurve in Python