Wie man einen Anderson-Darling-Test in R durchführt

Ein Anderson-Darling-Test ist ein Anpassungstest, der misst, wie gut Ihre Daten zu einer bestimmten Verteilung passen. Dieser Test wird am häufigsten verwendet, um festzustellen, ob Ihre Daten einer Normalverteilung folgen oder nicht.

Diese Art von Test ist nützlich, um die Normalverteilung zu testen. Dies ist eine häufige Annahme, die in vielen statistischen Tests verwendet wird, einschließlich Regression, ANOVA, t-Tests und vielen anderen.

Beispiel: Anderson-Darling-Test in R

Um einen Anderson-Darling-Test in R durchzuführen, können wir die Funktion ad.test() in der Nortest-Bibliothek verwenden.

Der folgende Code zeigt, wie ein AD-Test durchgeführt wird, um zu testen, ob ein Vektor mit 100 Werten einer Normalverteilung folgt oder nicht:

#Installieren (falls nicht bereits installiert) und Laden der Nortest-Bibliothek
install.packages('nortest')
library(nortest)

#Machen Sie dieses Beispiel reproduzierbar
set.seed(1)

#definierter Vektor mit 100 normalverteilten Werten
x <- rnorm(100, 0, 1)

#Anderson-Darling Test zum Testen auf Normalverteilung durchführen
ad.test(x)

#   Anderson-Darling normality test
#
#data:  x
#A = 0.16021, p-value = 0.9471

Dieser Test gibt zwei Werte zurück:

• A: die Teststatistik.
• p-Wert: Der entsprechende p-Wert der Teststatistik.

Die Nullhypothese für den AD–Test ist, dass die Daten einer Normalverteilung folgen. Wenn unser p-Wert für den Test unter unserem Signifikanzniveau liegt (übliche Auswahlmöglichkeiten sind 0,10, 0,05 und 0,01), können wir die Nullhypothese ablehnen und daraus schließen, dass wir genügend Beweise haben, um zu sagen, dass unsere Daten keinem Normalwert folgen Verteilung.

In diesem Fall beträgt unser p-Wert 0,9471. Da dies nicht unter unserem Signifikanzniveau liegt (sagen wir 0,05), haben wir nicht genügend Beweise, um die Nullhypothese abzulehnen. Man kann mit Sicherheit sagen, dass unsere Daten einer Normalverteilung folgen. Dies ist sinnvoll, wenn man bedenkt, dass wir mit der Funktion rnorm() in R 100 Werte generiert haben, die einer Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 folgen.

Angenommen, wir generieren stattdessen einen Vektor mit 100 Werten, die einer gleichmäßigen Verteilung zwischen 0 und 1 folgen. Wir können erneut einen AD-Test durchführen, um festzustellen, ob diese Daten einer Normalverteilung folgen:

#Machen Sie dieses Beispiel reproduzierbar
set.seed (1)

#definierter Vektor mit 100 Werten, die gleichmäßig verteilt sind
x <- runif (100, 0, 1)

#conduct Anderson-Darling Test zum Testen auf Normalverteilung
ad.test (x)

# Anderson-Darling-Test auf Normalverteilung
#
#data: x
#A = 1,1472, p-Wert = 0,005086

Unsere Teststatistik A beträgt 1,1472 und der entsprechende p-Wert 0,005086. Da unser p-Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen und daraus schließen, dass wir genügend Beweise haben, um zu sagen, dass diese Daten keiner Normalverteilung folgen. Dies entspricht dem erwarteten Ergebnis, da wir wissen, dass unsere Daten tatsächlich einer gleichmäßigen Verteilung folgen.

Durchführen eines Anderson-Darling-Tests an einer Spalte eines Dataframes in R

Wir können auch einen AD-Test für eine bestimmte Spalte eines Dataframes in R durchführen. Betrachten Sie beispielsweise den integrierten Iris-Datensatz:

#Die ersten sechs Zeilen des Iris- Datensatzes anzeigen
head(iris)

#  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#1          5.1         3.5          1.4         0.2  setosa
#2          4.9         3.0          1.4         0.2  setosa
#3          4.7         3.2          1.3         0.2  setosa
#4          4.6         3.1          1.5         0.2  setosa
#5          5.0         3.6          1.4         0.2  setosa
#6          5.4         3.9          1.7         0.4  setosa

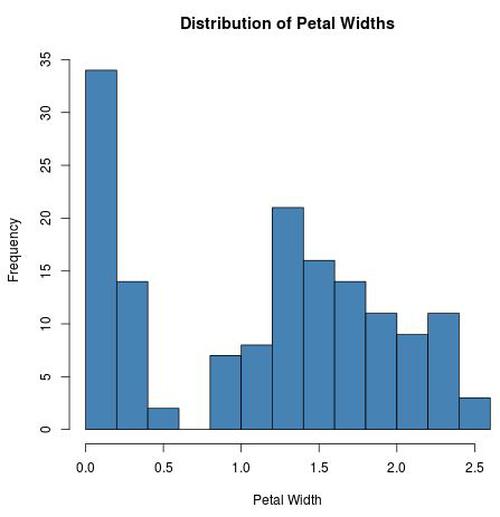
Angenommen, wir möchten wissen, ob die Variable Petal.Width normal verteilt ist oder nicht. Wir könnten zuerst ein Histogramm erstellen, um die Verteilung der Werte zu visualisieren:

hist(iris$Petal.Width, col = 'steelblue', main = 'Distribution of Petal Widths',
     xlab = 'Petal Width')

Die Daten scheinen nicht normal verteilt zu sein. Um dies zu bestätigen, können wir einen AD-Test durchführen, um formal zu testen, ob die Daten normal verteilt sind oder nicht:

#Anderson-Darling Test zum Testen auf Normalverteilung durchführen
ad.test(iris$Petal.Width)

#   Anderson-Darling normality test
#
#data:  iris$Petal.Width
#A = 5.1057, p-value = 1.125e-12

Der p-Wert des Tests liegt unter 0,05, daher haben wir genügend Beweise, um die Nullhypothese abzulehnen und zu dem Schluss zu kommen, dass Petal.Width keiner Normalverteilung folgt.