Kann ein z-Wert negativ sein?

In der Statistik gibt ein z-Wert (auch: z-Score) an, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist. Wir verwenden die folgende Formel, um einen Z-Score zu berechnen:

z = (X – μ) / σ

Dabei ist X der Wert, den wir analysieren, μ der Mittelwert und σ die Standardabweichung.

Ein z-Wert kann positiv, negativ oder gleich Null sein.

Ein positiver z-Wert zeigt an, dass ein bestimmter Wert größer als der Mittelwert ist, ein negativer z-Wert zeigt an, dass ein bestimmter Wert kleiner als der Mittelwert ist, und ein z-Wert von Null zeigt an, dass ein bestimmter Wert gleich dem Mittelwert ist.

Einige Beispiele sollten dies verdeutlichen.

Beispiele: Berechnung eines z-Scores

Angenommen, wir haben den folgenden Datensatz, der die Höhe (in Zoll) einer bestimmten Pflanzengruppe anzeigt:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

Der Stichprobenmittelwert dieses Datensatzes beträgt 13 und die Standardabweichung der Stichprobe beträgt 5,51.

1. Suchen Sie den z-Wert für den Wert „8“ in diesem Datensatz.

So berechnen Sie den Z-Score:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Dies bedeutet, dass der Wert „8“ 0,91 Standardabweichungen unter dem Mittelwert liegt.

2. Suchen Sie den z-Wert für den Wert „13“ in diesem Datensatz.

So berechnen Sie den z-Wert:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Dies bedeutet, dass der Wert „13“ genau dem Mittelwert entspricht.

3. Suchen Sie den z-Wert für den Wert „20“ in diesem Datensatz.

So berechnen Sie den z-Wert:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Dies bedeutet, dass der Wert „20“ 1,28 Standardabweichungen über dem Mittelwert liegt.

Wie man z-Wert interpretiert

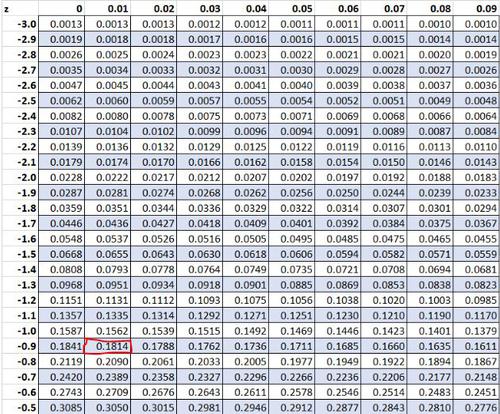
Eine z-Tabelle gibt an, wie viel Prozent der Werte unter bestimmte z-Werte fallen. Einige Beispiele sollten dies verdeutlichen.

Beispiel 1: Negative z-Werte

Zuvor haben wir festgestellt, dass der Rohwert „8“ in unserem Datensatz einen Z-Score von -0,91 aufweist. Nach der z-Tabelle fallen 18,14% der Werte unter diesen Wert.

Beispiel 2: z-Werte gleich Null

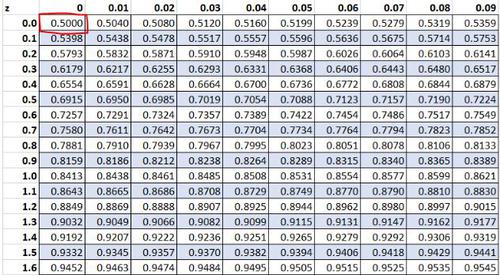
Zuvor haben wir festgestellt, dass der Rohwert „13“ in unserem Datensatz einen z-Wert von 0 aufweist. Gemäß der z-Tabelle fallen 50,00% der Werte unter diesen Wert.

Beispiel 3: Positive z-Werte

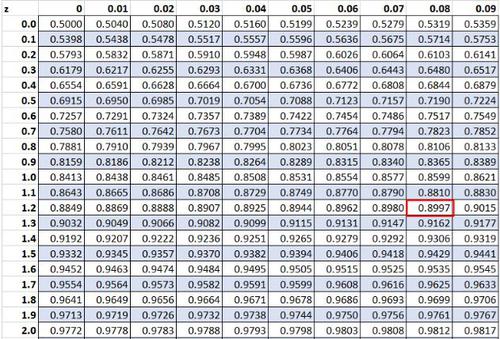
Zuvor haben wir festgestellt, dass der Rohwert „20“ in unserem Datensatz einen Z-Score von 1,28 aufweist. Gemäß der z-Wert fallen 89,97% der Werte unter diesen Wert.

Fazit

z-Werte können einen beliebigen Wert zwischen negativer Unendlichkeit und positiver Unendlichkeit annehmen, aber die meisten z-Werte liegen innerhalb von 2 Standardabweichungen vom Mittelwert. In der Statistik gibt es tatsächlich eine Regel, die als die 68–95–99.7 Regel bekannt ist und besagt, dass für einen bestimmten Datensatz mit einer Normalverteilung:

• 68% der Datenwerte liegen innerhalb einer Standardabweichung vom Mittelwert.
• 95% der Datenwerte liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• 99,7% der Datenwerte liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Je höher der Absolutwert eines z-Wertes ist, desto weiter ist ein Rohwert vom Mittelwert des Datensatzes entfernt. Je niedriger der Absolutwert eines z-Wertes ist, desto näher liegt ein Rohwert am Mittelwert des Datensatzes.

Verwandte Themen: So wenden Sie die 68–95–99.7 Regel in Excel an