Welch-Test in R - so geht's

Der Welch-Test wird verwendet, um die Mittelwerte zwischen zwei unabhängigen Gruppen zu vergleichen, wenn nicht angenommen wird, dass die beiden Gruppen gleiche Varianzen aufweisen.

Um den Welch-Test in R durchzuführen, können wir die Funktion t.test() verwenden, die die folgende Syntax verwendet:

t.test(x, y, alternative = c(“two.sided”, “less”, “greater”))

wo:

• x: Ein numerischer Vektor von Datenwerten für die erste Gruppe
• y: Ein numerischer Vektor von Datenwerten für die zweite Gruppe
• alternative: Die alternative Hypothese für den Test. Die Standardeinstellung ist zweiseitig.

Das folgende Beispiel zeigt, wie diese Funktion verwendet wird, um den Welch-Test in R durchzuführen.

Beispiel: Welch-Test in R

Ein Lehrer möchte die Prüfungsergebnisse von 12 Schülern, die ein Prüfungsvorbereitungsheft zur Vorbereitung auf eine Prüfung verwendet haben, mit 12 Schülern vergleichen, die dies nicht getan haben.

Die folgenden Vektoren zeigen die Prüfungsergebnisse für die Schüler in jeder Gruppe:

booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

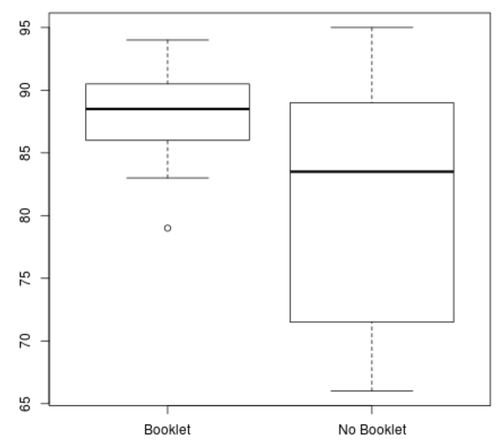
Bevor wir einen Welch-Test durchführen, können wir zunächst Boxplots erstellen, um die Verteilung der Punktzahlen für jede Gruppe zu visualisieren:

boxplot(booklet, no_booklet, names=c("Booklet","No Booklet"))

Wir können deutlich sehen, dass die Gruppe „Booklet“ einen höheren Mittelwert und eine geringere Varianz der Punktzahlen aufweist.

Um formal zu testen, ob die Durchschnittswerte zwischen den Gruppen signifikant unterschiedlich sind oder nicht, können wir den Welch-Test durchführen:

#Welch-Test durchführen
t.test(booklet, no_booklet)

    Welch Two Sample t-test

data:  booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667  80.83333 

Aus der Ausgabe können wir erkennen, dass die t-Teststatistik 2,2361 und der entsprechende p-Wert 0,04171 beträgt.

Da dieser p-Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen und daraus schließen, dass es einen statistisch signifikanten Unterschied in den mittleren Prüfungsergebnissen zwischen den beiden Gruppen gibt.

Die Funktion t.test() liefert uns auch folgende Informationen:

• Das 95%-Konfidenzintervall für die Differenz der mittleren Prüfungsergebnisse zwischen den beiden Gruppen beträgt [0,3048, 13,8618 ].
• Die durchschnittliche Prüfungspunktzahl der ersten Gruppe beträgt 87,91667.
• Die durchschnittliche Prüfungspunktzahl der zweiten Gruppe beträgt 80,83333.

Die vollständige Dokumentation zur Funktion t.test() finden Sie hier.