Was genau sind Zufallsvariablen?

Eine Zufallsvariable (auch Zufallsgröße), die typischerweise als X bezeichnet wird, ist eine Variable, deren mögliche Werte Ergebnisse eines zufälligen Prozesses sind. Es gibt zwei Arten von Zufallsvariablen: diskret und kontinuierlich.

Diskrete Zufallsvariablen

Eine diskrete Zufallsvariable ist eine Variable, die nur eine zählbare Anzahl unterschiedlicher Werte wie 0, 1, 2, 3, 4, 5… 100, 1 Million usw. annehmen kann. Einige Beispiele für diskrete Zufallsvariablen umfassen:

• Die Häufigkeit, mit der eine Münze nach 20-maligem Umwerfen auf Zahl landet.
• Die Häufigkeit, mit der ein Würfel auf der Zahl 4 landet, nachdem er 100 Mal gewürfelt wurde.
• Die Anzahl der fehlerhaften Widgets in einer Box mit 50 Widgets.

Eine Wahrscheinlichkeitsverteilung für eine diskrete Zufallsvariable gibt Auskunft über die Wahrscheinlichkeit, dass die Zufallsvariable bestimmte Werte annimmt.

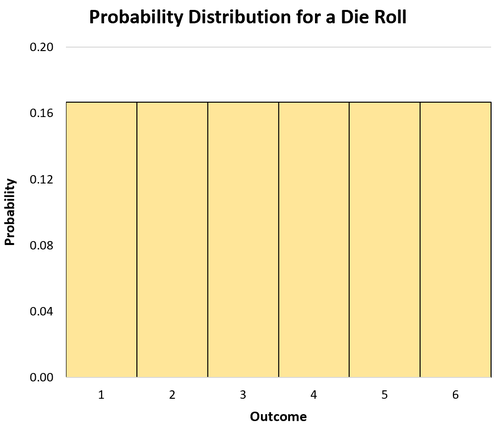
Nehmen wir zum Beispiel an, wir würfeln einmal einen fairen Würfel. Wenn wir X die Wahrscheinlichkeit bezeichnen lassen, dass der Würfel auf einer bestimmten Zahl landet, kann die Wahrscheinlichkeitsverteilung wie folgt geschrieben werden:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Hinweis:
Damit eine Wahrscheinlichkeitsverteilung gültig ist, muss sie die folgenden zwei Kriterien erfüllen:

1. Die Wahrscheinlichkeit für jedes Ergebnis muss zwischen 0 und 1 liegen.
2. Die Summe aller Wahrscheinlichkeiten muss 1 ergeben.

Beachten Sie, dass die Wahrscheinlichkeitsverteilung für den Würfelwurf beide Kriterien erfüllt:

1. Die Wahrscheinlichkeit für jedes Ergebnis liegt zwischen 0 und 1.
2. Die Summe aller Wahrscheinlichkeiten ergibt 1.

Wir können ein Histogramm verwenden, um die Wahrscheinlichkeitsverteilung zu visualisieren:

Eine kumulative Wahrscheinlichkeitsverteilung für eine diskrete Zufallsvariable gibt die Wahrscheinlichkeit an, dass die Variable einen Wert annimmt, der gleich oder kleiner als ein Wert ist.

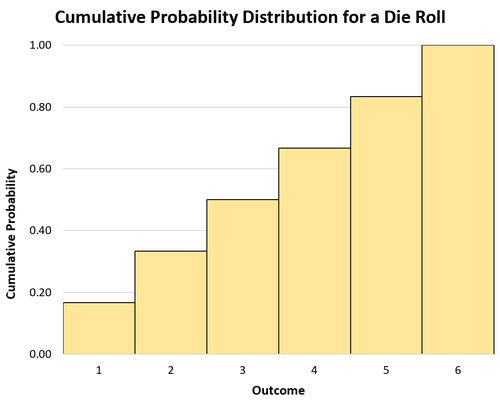
Zum Beispiel würde die kumulative Wahrscheinlichkeitsverteilung für einen Würfelwurf folgendermaßen aussehen:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

Die Wahrscheinlichkeit, dass der Würfel auf einer Eins oder weniger landet, beträgt einfach 1/6, da er nicht auf einer Zahl kleiner als Eins landen kann.

Die Wahrscheinlichkeit, dass es auf zwei oder weniger landet, ist P(X = 1) + P(X = 2) = 1/6 + 1/6 = 2/6.

In ähnlicher Weise ist die Wahrscheinlichkeit, dass es auf einer Drei oder weniger landet, P(X = 1) + P(X = 2) + P(X = 3) = 1/6 + 1/6 + 1/6 = 3/6, und so weiter.

Wir können auch ein Histogramm verwenden, um die kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

Kontinuierliche Zufallsvariablen

Eine kontinuierliche Zufallsvariable ist eine Variable, die unendlich viele mögliche Werte annehmen kann. Einige Beispiele für kontinuierliche Zufallsvariablen sind:

• Gewicht eines Tieres
• Größe einer Person
• Zeitaufwand für einen Marathon

Zum Beispiel könnte die Größe einer Person 60,2 Zoll, 65,2344 Zoll, 70,431222 Zoll usw. betragen. Es gibt unendlich viele mögliche Werte für die Größe.

Faustregel:

Wenn Sie die Anzahl der Ergebnisse zählen können, arbeiten Sie mit einer diskreten Zufallsvariablen – z. Zählen, wie oft eine Münze auf Köpfen landet.

Wenn Sie jedoch das Ergebnis messen können, arbeiten Sie mit einer kontinuierlichen Zufallsvariablen – z. Messen von Größe, Gewicht, Zeit usw.

Eine Wahrscheinlichkeitsverteilung für eine kontinuierliche Zufallsvariable gibt Auskunft über die Wahrscheinlichkeit, dass die Zufallsvariable bestimmte Werte annimmt. Im Gegensatz zu einer Wahrscheinlichkeitsverteilung für diskrete Zufallsvariablen kann eine Wahrscheinlichkeitsverteilung für eine kontinuierliche Zufallsvariable jedoch nur verwendet werden, um die Wahrscheinlichkeit anzugeben, mit der die Variable einen Wertebereich annimmt.

Angenommen, wir möchten wissen, mit welcher Wahrscheinlichkeit ein Burger aus einem bestimmten Restaurant ein Viertel Pfund (0,25 lbs) wiegt. Da das Gewicht eine stetige Variable ist, kann es unendlich viele Werte annehmen.

Zum Beispiel könnte ein gegebener Burger tatsächlich 0,250001 Pfund oder 0,24 Pfund oder 0,2488 Pfund wiegen. Die Wahrscheinlichkeit, dass ein bestimmter Burger genau 0,25 Pfund wiegt, ist im Wesentlichen Null.

Daher könnten wir nur eine Wahrscheinlichkeitsverteilung verwenden, um die Wahrscheinlichkeit zu ermitteln, dass ein Burger weniger als 0,25 lbs, mehr als 0,25 lbs oder zwischen einem bestimmten Bereich (z. B. zwischen 0,23 lbs und 0,27 lbs) wiegt.