Untererfassung-Verzerrung: Definition + Beispiele

Untererfassung-Verzerrung ist die Verzerrung, die auftritt, wenn einige Mitglieder einer Population in der Stichprobe unzureichend vertreten sind.

Diese Art von Verzerrung tritt häufig bei willkürlichen Stichproben auf, bei denen man eine Stichprobe erhebt, die leicht zu erhalten ist, bei der es aber oft zu einer Untererfassung bestimmter Mitglieder einer Population kommt.

Warum ist Untererfassung-Verzerrung ein Problem?

Untererfassung-Verzerrung ist ein Problem, weil es die Stichprobe für die Grundgesamtheit nicht repräsentativ ist. Der Sinn der Datenerhebung für eine Stichprobe besteht darin, Daten auf eine Art und Weise zu erhalten, die schneller und einfacher ist als die Datenerhebung für die gesamte Bevölkerung, und in der Lage zu sein, die Ergebnisse aus der Stichprobe auf die größere Bevölkerung zu extrapolieren.

Um die Ergebnisse extrapolieren zu können, muss die Stichprobe jedoch repräsentativ für unsere Grundgesamtheit sein. Idealerweise sollte unsere Stichprobe eine "Mini"-Version der Grundgesamtheit sein. Leider kann die Untererfassung dazu führen, dass sich die Personen in unserer Stichprobe erheblich von den Personen in der Grundgesamtheit unterscheiden.

Angenommen, Forscher wollen wissen, was die Bürger einer bestimmten Stadt über ein mögliches neues Gesetz denken. Um Daten zu sammeln, gehen sie in eine nahe gelegene Bibliothek und fragen die Leute, die dort vorbeikommen, was sie von dem potenziellen neuen Gesetz halten. Obwohl dies eine bequeme Art der Datenerhebung ist, riskieren die Forscher eine Untererfassung verschiedener Arten von Menschen, darunter:

• Personen, die ans Haus gebunden sind
• Personen, die einfach nicht gerne in die Bibliothek gehen
• Menschen, die eine andere Bibliothek in einem anderen Teil der Stadt besuchen

Da diese Studie bestimmte Personengruppen ausschließt, ist es unwahrscheinlich, dass die Ergebnisse der Studie repräsentativ für die Bevölkerung sind.

Angenommen, die Menschen, die diese bestimmte Bibliothek besuchen, sind im Vergleich zum Rest der Bevölkerung weitaus wahrscheinlicher Befürworter des potenziellen neuen Gesetzes. Das bedeutet, dass die Ergebnisse der Umfrage den Anschein erwecken werden, dass ein großer Prozentsatz der Bürger dieser Stadt das potenzielle neue Gesetz unterstützt, obwohl die meisten Bürger dies nicht tun.

Das folgende Schaubild veranschaulicht dieses Problem: Nehmen wir an, die grünen Kreise stehen für Menschen, die für das neue Gesetz sind, während die roten Kreise Menschen darstellen, die gegen das neue Gesetz sind:

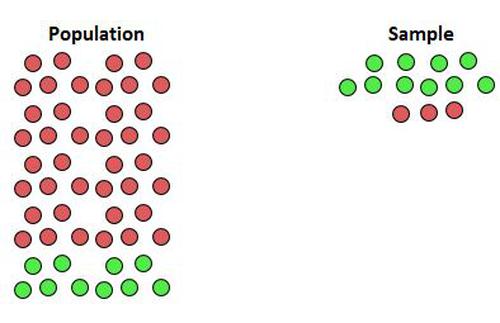
Beachten Sie, dass die meisten der Personen, die das neue Gesetz befürworten, in der Stichprobe enthalten sind, die Stichprobe jedoch nicht repräsentativ für die Gesamtbevölkerung ist. Die Ergebnisse der Umfrage würden zeigen, dass die meisten Menschen das neue Gesetz befürworten, obwohl dies in Wirklichkeit nicht der Fall ist.

Beispiele für Undercoverage Bias

Die folgenden Beispiele illustrieren mehrere Fälle, in denen eine Untererfassung auftreten kann.

Beispiel 1

Forscher wollen herausfinden, was die Bürger einer bestimmten Stadt über den Bau eines neuen Parks denken. Um Daten zu sammeln, besuchen die Forscher eine örtliche Bürgerversammlung und befragen die Menschen dort nach ihrer Meinung. Leider werden bei dieser Form der Zufallsstichprobe die folgenden Gruppen wahrscheinlich nicht ausreichend erfasst:

• Personen, die keinen Zugang zu Verkehrsmitteln haben, um zu den Bürgerversammlungen zu fahren
• Menschen, die nicht einmal wissen, dass Stadtversammlungen stattfinden
• Menschen, die abends arbeiten und einfach nicht an Stadtversammlungen teilnehmen können

Die Meinungen dieser Personen werden daher nicht in die Ergebnisse der Studie einfließen. Aufgrund dieser Untererfassung dieser spezifischen Gruppen ist es unwahrscheinlich, dass die Stichprobe repräsentativ für die Gesamtbevölkerung ist.

Beispiel 2

Forscher wollen wissen, wie viele Stunden pro Tag die Menschen in einem bestimmten Bezirk fernsehen. Um Daten für die Studie zu sammeln, wählen sie zufällig Namen aus einem örtlichen Telefonbuch aus und rufen die Leute an, um sie nach ihrem Fernsehkonsum zu fragen. Dabei handelt es sich um eine Form der Zufallsstichprobe, bei der es wahrscheinlich zu einer Untererfassung der folgenden Gruppen kommt:

• Sehr wohlhabende Menschen, die ihre Telefonnummern nicht in den örtlichen Telefonbüchern eintragen
• Junge Leute, die nur Mobiltelefone benutzen und ihre Nummern nicht in den örtlichen Telefonbüchern eintragen lassen

Der Fernsehkonsum von sehr wohlhabenden Menschen und jungen Menschen wird in dieser Studie also untererfasst. Aufgrund dieser Untererfassung dieser spezifischen Gruppen ist es unwahrscheinlich, dass die Stichprobe für die Gesamtbevölkerung repräsentativ ist.

Beispiel 3

Forscher wollen wissen, was die Bürger einer bestimmten Stadt von einem neuen Verkehrsgesetz halten und verteilen daher einen Fragebogen an Passanten in einem Einkaufszentrum. TDies ist eine Form der Zufallsstichprobe, bei der die folgenden Gruppen wahrscheinlich untererfasst werden:

• Personen, die keinen Zugang zu Verkehrsmitteln haben, um ins Einkaufszentrum zu gehen (und daher von Verkehrsgesetzen weitgehend unbeeinflusst sind)
• Menschen, die nicht gerne ins Einkaufszentrum gehen (und daher in verkehrsreichen Gegenden vielleicht nicht mit dem Auto fahren)
• Personen, die in ein anderes Einkaufszentrum in einer anderen Stadt gehen

Die Meinungen dieser Personen werden also nicht in die Ergebnisse der Studie einfließen. Aufgrund dieser Untererfassung dieser spezifischen Gruppen ist es unwahrscheinlich, dass die Stichprobe repräsentativ für die Gesamtbevölkerung ist.

Wie man eine Untererfassung verhindert

Untererfassung-Verzerrung tritt häufig als Folge von Zufallsstichproben auf. Um die Auswirkungen der Untererfassung zu beseitigen (oder zumindest zu minimieren), ist eine bessere Form der Stichprobenziehung die Verwendung einer einfachen Zufallsstichprobe.

Bei dieser Art von Stichprobe hat jedes Mitglied einer Grundgesamtheit die gleiche Chance, in die Stichprobe aufgenommen zu werden.

Der Vorteil dieses Ansatzes ist, dass einfache Zufallsstichproben in der Regel repräsentativ für die Grundgesamtheit sind, an der wir interessiert sind, da jedes Mitglied die gleiche Chance hat, in die Stichprobe aufgenommen zu werden.

Wenn wir diesen Ansatz anstelle von Zufallsstichproben verwenden, können wir sicherer sein, dass wir die Ergebnisse aus der Stichprobe auf die größere Grundgesamtheit extrapolieren können, da es wahrscheinlich ist, dass Mitglieder aus jeder (oder fast jeder) Gruppe der Grundgesamtheit in der Stichprobe enthalten sind.

Zusätzliche Ressourcen

• Beobachter-Verzerrung
• Selbstselektion-Verzerrung
• Verzerrung durch ausgelassene Variablen
• Schweigeverzerrung