So führen Sie t-Tests in Google Tabellen durch

Im Großen und Ganzen gibt es drei Arten von t-Tests:

• Einstichproben-t-Test
• Zweistichproben-t-Test
• t-Test mit gepaarten Stichproben

In dieser Anleitung finden Sie Beispiele für die Durchführung jedes dieser Tests in Google Tabellen.

Beispiel: Einstichproben-t-Test

Definition: Ein Einstichproben-t-Test wird verwendet, um zu testen, ob der Mittelwert einer Grundgesamtheit einem Wert entspricht oder nicht.

Beispiel: Ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Sie sammelt eine Zufallsstichprobe von 12 Pflanzen und notiert jede ihrer Höhen in Zoll.

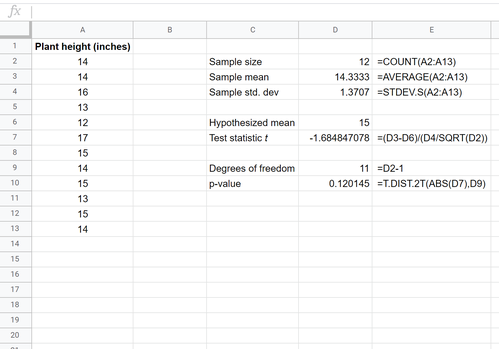
Der folgende Screenshot zeigt, wie Sie einen Einstichproben-t-Test durchführen, um zu bestimmen, ob die tatsächliche mittlere Größe der Population 15 Zoll beträgt:

Die beiden Hypothesen für diesen speziellen Einstichproben-t-Test lauten wie folgt:

H ₀: µ = 15 (die mittlere Höhe für diese Pflanzenart beträgt 15 Zoll)

H _A: µ ≠15 (die mittlere Höhe beträgt nicht 15 Zoll)

Da der p-Wert unseres Tests (0.120145) größer als alpha = 0.05 ist, verwerfen wir die Nullhypothese des Tests nicht. Wir haben keine ausreichenden Beweise dafür, dass die durchschnittliche Höhe dieser speziellen Pflanzenart von 15 Zoll abweicht.

Beispiel: Zweistichproben-t-Test

Definition: Ein Zweistichproben-t-Test wird verwendet, um zu testen, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.

Beispiel: Forscher wollen wissen, ob zwei verschiedene Pflanzenarten in einem bestimmten Land die gleiche mittlere Höhe haben oder nicht. Sie sammeln eine Zufallsstichprobe von 20 Pflanzen jeder Art und erfassen jede Pflanzenhöhe in Zoll.

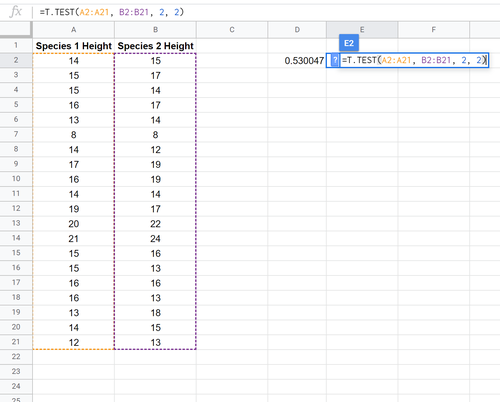
Der folgende Screenshot zeigt, wie Sie mit der Funktion T.TEST() einen Zweistichproben-t-Test durchführen, um zu bestimmen, ob die mittleren Höhen der beiden Grundgesamtheiten gleich sind:

Hinweis: Es ist auch möglich, einen einseitigen Zweistichproben-t-Test durchzuführen, mit oder ohne die Annahme, dass beide Stichproben die gleiche Varianz aufweisen. In der T.TEST-Dokumentation erfahren Sie, wie Sie die Annahmen für den Test anpassen.

Die beiden Hypothesen für diesen Zweistichproben-t-Test lauten wie folgt:

H ₀: μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)

H ₁: μ ₁ ≠ μ ₂ (die Mittelwerte der beiden Grundgesamtheiten sind nicht gleich)

Da der p-Wert unseres Tests (0,530047) größer als alpha = 0,05 ist, verwerfen wir die Nullhypothese des Tests nicht. Wir haben keine ausreichenden Beweise dafür, dass die durchschnittliche Höhe dieser speziellen Pflanzenart von 15 Zoll abweicht.

Beispiel: t-Test mit gepaarten Stichproben

Definition: Ein t-Test mit gepaarten Stichproben wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jede Beobachtung in einer Stichprobe mit einer Beobachtung in der anderen Stichprobe gepaart werden kann.

Beispiel: Wir wollen wissen, ob ein Studiengang die Leistung der Studierenden in einer bestimmten Prüfung maßgeblich beeinflusst. Um dies zu testen, lassen wir 20 Schüler einer Klasse einen Vortest machen. Anschließend lassen wir jeden der Studierenden für zwei Wochen am Studienprogramm teilnehmen. Anschließend wiederholen die Schüler einen Test mit ähnlichem Schwierigkeitsgrad.

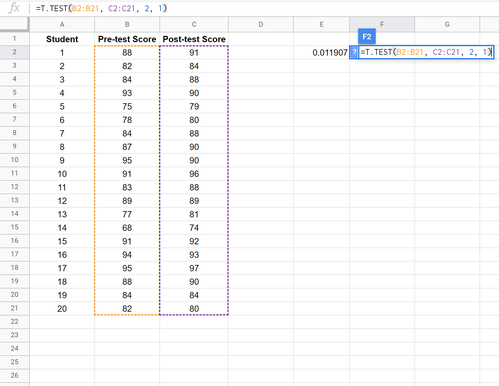
Der folgende Screenshot zeigt, wie Sie einen t-Test mit gepaarten Stichproben durchführen, um die Differenz zwischen den Mittelwerten des ersten und zweiten Tests zu vergleichen:

Hinweis: Es ist auch möglich, einen einseitigen Zweistichproben-t-Test durchzuführen, mit oder ohne die Annahme, dass beide Stichproben die gleiche Varianz aufweisen. In der T.TEST-Dokumentation erfahren Sie, wie Sie die Annahmen für den Test anpassen.

Die beiden Hypothesen für diesen t-Test mit gepaarten Stichproben lauten wie folgt:

H ₀: μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)

H ₁: μ ₁ ≠ μ ₂ (die Mittelwerte der beiden Grundgesamtheiten sind nicht gleich)

Da der p-Wert unseres Tests (0,011907) kleiner als alpha = 0,05 ist, lehnen wir die Nullhypothese des Tests ab. Wir haben genügend Beweise dafür, dass es einen statistisch signifikanten Unterschied zwischen dem mittleren Vor- und Nachtestergebnis gibt.