t-Test für gepaarte Stichproben: Definition, Formel und Beispiel

Ein t-Test mit gepaarten Stichproben wird verwendet, um die Mittelwerte von zwei Stichproben zu vergleichen, wenn jede Beobachtung in einer Probe mit einer Beobachtung in der anderen Probe gepaart werden kann.

In diesem Tutorial wird Folgendes erklärt:

• Die Motivation für die Durchführung eines t-Tests mit gepaarten Stichproben.
• Die Formel zur Durchführung eines gepaarten Stichproben-t-Tests.
• Die Annahmen, die erfüllt sein sollten, um einen t-Test mit gepaarten Stichproben durchzuführen.
• Ein Beispiel für die Durchführung eines t-Tests mit gepaarten Stichproben.

t-Test mit gepaarten Stichproben: Motivation

Ein gepaarter Stichproben-t-Test wird üblicherweise in zwei Szenarien verwendet:

1. Vor und nach einer Behandlung wird eine Messung an einem Probanden durchgeführt – z. B. wird der maximale vertikale Sprung von College-Basketballspielern vor und nach der Teilnahme an einem Trainingsprogramm gemessen.

2. Eine Messung wird unter zwei verschiedenen Bedingungen durchgeführt – z. B. wird die Reaktionszeit eines Patienten an zwei verschiedenen Medikamenten gemessen.

In beiden Fällen sind wir daran interessiert, die mittlere Messung zwischen zwei Gruppen zu vergleichen, in denen jede Beobachtung in einer Probe mit einer Beobachtung in der anderen Probe gepaart werden kann.

t-Test für gepaarte Stichproben: Formel

Ein t-Test mit gepaarten Stichproben verwendet immer die folgende Nullhypothese:

• H ₀: μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)

Die alternative Hypothese kann entweder zweiseitig, linksseitig oder rechtsseitig sein:

• H ₁ (zweiseitig): μ ₁ ≠ μ ₂ (die beiden Populationsmittelwerte sind nicht gleich)
• H ₁ (linksseitig): μ ₁ <μ ₂ (Mittelwert der Population 1 ist kleiner als Mittelwert der Population 2)
• H ₁ (rechtsseitig): μ ₁ > μ ₂ (Mittelwert der Population 1 ist größer als Mittelwert der Population 2)

Wir verwenden die folgende Formel, um die Teststatistik t zu berechnen:

t = x _diff / (s _diff / √n)

wo:

• x _diff: Stichprobenmittelwert der Unterschiede
• s: Stichprobenstandardabweichung der Differenzen
• n: Stichprobengröße (d.h. Anzahl der Paare)

Wenn der p-Wert, der der Teststatistik t mit (n-1) Freiheitsgraden entspricht, kleiner als das von Ihnen gewählte Signifikanzniveau ist (allgemeine Auswahlmöglichkeiten sind 0,10, 0,05 und 0,01), können Sie die Nullhypothese ablehnen.

t-Test für gepaarte Stichproben: Annahmen

Damit die Ergebnisse eines t-Tests mit gepaarten Stichproben gültig sind, sollten die folgenden Annahmen erfüllt sein:

• Die Teilnehmer sollten zufällig aus der Bevölkerung ausgewählt werden.
• Die Unterschiede zwischen den Paaren sollten ungefähr normal verteilt sein.
• Es sollte keine extremen Ausreißer in den Unterschieden geben.

t-Test für gepaarte Stichproben : Beispiel

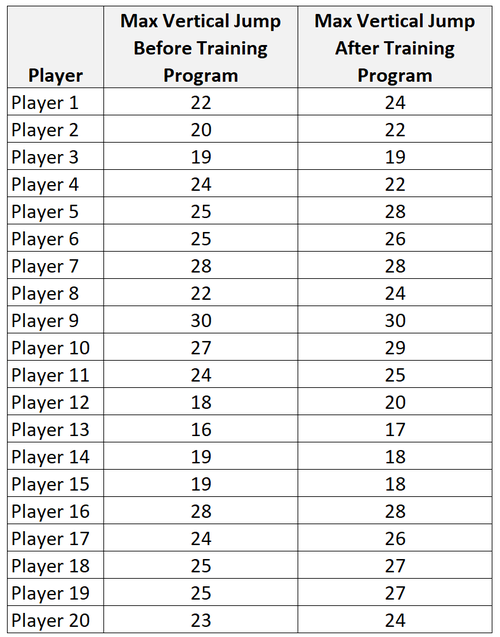
Angenommen, wir möchten wissen, ob ein bestimmtes Trainingsprogramm den maximalen vertikalen Sprung (in Zoll) von College-Basketballspielern erhöhen kann oder nicht. Um dies zu testen, können wir eine einfache Zufallsstichprobe von 20 College-Basketballspielern rekrutieren und jeden ihrer maximalen vertikalen Sprünge messen. Dann kann jeder Spieler das Trainingsprogramm einen Monat lang verwenden und dann am Ende des Monats erneut seinen maximalen vertikalen Sprung messen.

Um festzustellen, ob das Trainingsprogramm tatsächlich einen Einfluss auf den maximalen vertikalen Sprung hatte oder nicht, führen wir einen gepaarten Stichproben-t-Test mit einem Signifikanzniveau von α = 0,05 durch, indem wir die folgenden Schritte ausführen:

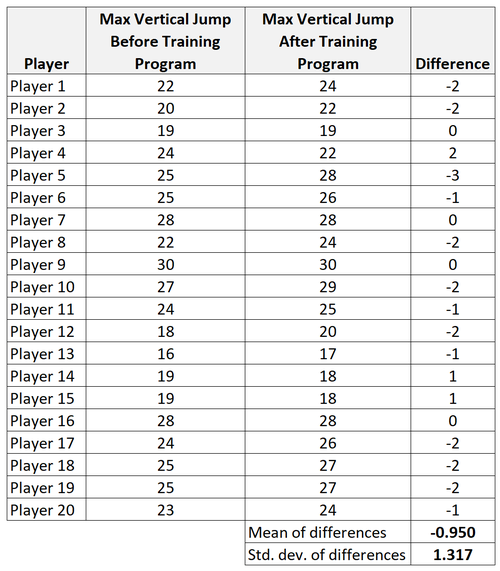
Schritt 1: Berechnen Sie die Zusammenfassungsdaten für die Unterschiede.

• x _diff: Stichprobenmittelwert der Differenzen = -0,95
• s: Stichprobenstandardabweichung der Differenzen = 1,317
• n: Stichprobengröße (d.h. Anzahl der Paare) = 20

Schritt 2: Definieren Sie die Hypothesen.

Wir werden den gepaarten Stichproben-t-Test mit den folgenden Hypothesen durchführen:

• H ₀: μ ₁ = μ ₂ (die beiden Populationsmittelwerte sind gleich)
• H ₁: μ ₁ ≠ μ ₂ (die beiden Populationsmittelwerte sind nicht gleich)

Schritt 3: Berechnen Sie die Teststatistik t.

t = x _diff / (s _diff / √n) = -0,95 / (1,317 / √ 20) = -3,226

Schritt 4: Berechnen Sie den p-Wert der Teststatistik t.

Rechnet man es nach, beträgt der mit t = -3,226 und Freiheitsgraden = n-1 = 20-1 = 19 verbundene p-Wert 0,00445.

Schritt 5: Ziehen Sie eine Schlussfolgerung.

Da dieser p-Wert kleiner als unser Signifikanzniveau α = 0,05 ist, lehnen wir die Nullhypothese ab. Wir haben genügend Beweise, um zu sagen, dass der mittlere maximale vertikale Sprung der Spieler vor und nach der Teilnahme am Trainingsprogramm unterschiedlich ist.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie ein t-Test mit gepaarten Stichproben mit verschiedenen statistischen Programmen durchgeführt wird:

So führen Sie einen Paired Samples-t-Test in SPSS durch
Durchführen eines t-Tests mit gepaarten Proben in Stata
So führen Sie einen t-Test für gepaarte Proben auf einem TI-84-Rechner durch
Durchführen eines t-Tests mit gepaarten Proben in R
Durchführen eines t-Tests mit gepaarten Beispielen in Python