Was ist eine Störvariable? (Definition & Beispiel)

In jedem Experiment gibt es zwei Hauptvariablen:

Die unabhängige Variable: die Variable, die ein Experimentator verändert oder kontrolliert, um die Auswirkungen auf die abhängige Variable zu beobachten.

Die abhängige Variable: die Variable, die in einem Experiment gemessen wird und von der unabhängigen Variable "abhängig" ist.

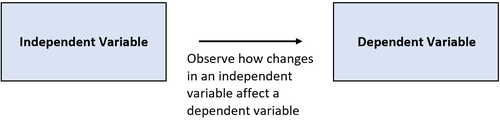
Forscher sind oft daran interessiert zu verstehen, wie sich Veränderungen der unabhängigen Variable auf die abhängige Variable auswirken.

Es gibt jedoch manchmal eine dritte Variable, die nicht berücksichtigt wird und die die Beziehung zwischen den beiden untersuchten Variablen beeinflussen kann.

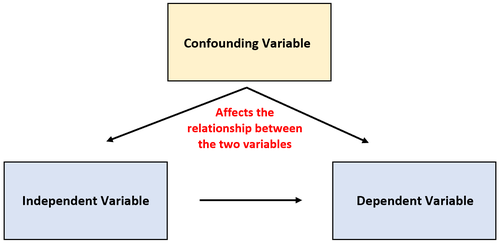
Diese Art von Variablen wird als Störvariable bezeichnet und kann die Ergebnisse einer Studie verfälschen und den Anschein erwecken, dass es eine Art von Ursache-Wirkungs-Beziehung zwischen zwei Variablen gibt, die in Wirklichkeit nicht existiert.

Begründungsvariable: Eine Variable, die nicht in einem Experiment enthalten ist, aber die Beziehung zwischen den beiden Variablen in einem Experiment beeinflusst.

Diese Art von Variablen kann die Ergebnisse eines Experiments verfälschen und zu unzuverlässigen Ergebnissen führen.

Angenommen, ein Forscher sammelt Daten über den Verkauf von Speiseeis und Haiangriffe und stellt fest, dass die beiden Variablen stark korreliert sind. Bedeutet dies, dass ein erhöhter Eiscremeverkauf zu mehr Hai-Angriffen führt?

Das ist unwahrscheinlich. Die wahrscheinlichere Ursache ist die Störvariable Temperatur. Wenn es draußen wärmer ist, kaufen mehr Menschen Eiscreme und mehr Menschen gehen ins Meer.

Voraussetzungen für Störvariablen

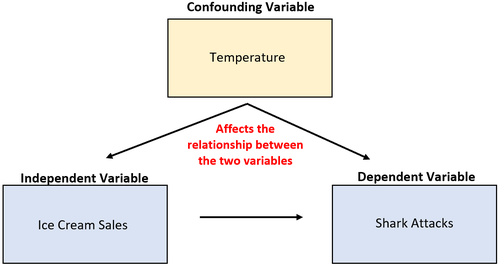
Damit eine Variable als Störvariable gilt, muss sie folgende Anforderungen erfüllen:

1. Sie muss mit der unabhängigen Variable korreliert sein.

Im vorangegangenen Beispiel korrelierte die Temperatur mit der unabhängigen Variable des Eiscremeverkaufs. Insbesondere werden wärmere Temperaturen mit höheren Eisverkäufen und kühlere Temperaturen mit niedrigeren Verkäufen in Verbindung gebracht.

2. Es muss ein kausaler Zusammenhang mit der abhängigen Variable bestehen.

Im vorherigen Beispiel hatte die Temperatur eine direkte kausale Wirkung auf die Anzahl der Haiangriffe. Insbesondere führen wärmere Temperaturen dazu, dass mehr Menschen ins Meer gehen, was die Wahrscheinlichkeit von Hai-Angriffen direkt erhöht.

Warum sind Störvariablen problematisch?

Verstreuungsvariablen sind aus zwei Gründen problematisch:

1. Störvariablen können den Anschein erwecken, dass Ursache-Wirkungs-Beziehungen bestehen, obwohl dies nicht der Fall ist.

In unserem vorherigen Beispiel ließ die Störvariable Temperatur den Anschein erwecken, dass eine kausale Beziehung zwischen dem Verkauf von Speiseeis und Hai-Angriffen besteht.

Wir wissen jedoch, dass der Verkauf von Speiseeis keine Haiattacken verursacht. Die Störvariable der Temperatur hat es nur so aussehen lassen.

2. Störvariablen können die wahre Ursache-Wirkungs-Beziehung zwischen Variablen verschleiern.

Angenommen, wir untersuchen die Fähigkeit von Sport, den Blutdruck zu senken. Eine mögliche Störvariable ist das Ausgangsgewicht, das mit der körperlichen Betätigung korreliert und einen direkten kausalen Effekt auf den Blutdruck hat.

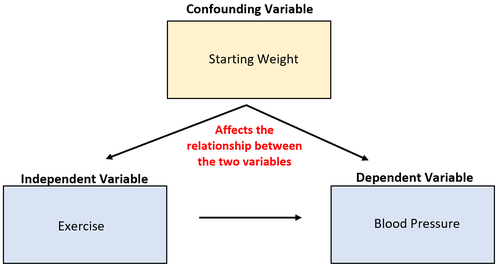
Eine erhöhte körperliche Aktivität kann zwar zu einem niedrigeren Blutdruck führen, aber auch das Ausgangsgewicht einer Person hat einen großen Einfluss auf die Beziehung zwischen diesen beiden Variablen.

Basisvariablen & Interne Validität

Technisch gesehen beeinflussen Störvariablen die interne Validität einer Studie, die sich darauf bezieht, wie valide es ist, Veränderungen in der abhängigen Variable auf Veränderungen in der unabhängigen Variable zurückzuführen.

Wenn Störvariablen vorhanden sind, können wir nicht immer mit absoluter Sicherheit sagen, dass die Veränderungen, die wir bei der abhängigen Variable beobachten, eine direkte Folge von Veränderungen bei der unabhängigen Variable sind.

Wie man den Effekt von Störvariablen reduziert

Es gibt mehrere Möglichkeiten, den Effekt von Störvariablen zu reduzieren, darunter die folgenden Methoden:

1. Zufällige Zuweisung

Zufallszuweisung bezieht sich auf den Prozess der zufälligen Zuweisung von Personen in einer Studie entweder zu einer Behandlungs- oder einer Kontrollgruppe.

Angenommen, wir wollen die Wirkung einer neuen Pille auf den Blutdruck untersuchen. Wenn wir 100 Personen für die Teilnahme an der Studie rekrutieren, könnten wir einen Zufallszahlengenerator verwenden, um 50 Personen nach dem Zufallsprinzip einer Kontrollgruppe (keine Pille) und 50 Personen einer Behandlungsgruppe (neue Pille) zuzuordnen.

Durch die Verwendung von Zufallszuweisungen erhöhen wir die Wahrscheinlichkeit, dass die beiden Gruppen annähernd ähnliche Merkmale aufweisen, was bedeutet, dass jeder Unterschied, den wir zwischen den beiden Gruppen beobachten, auf die Behandlung zurückgeführt werden kann.

Das bedeutet, dass die Studie interne Validität haben sollte - es ist valide, etwaige Unterschiede im Blutdruck zwischen den Gruppen der Pille selbst zuzuschreiben und nicht den Unterschieden zwischen den Personen in den Gruppen.

2. Block-Statistiken

Block-Statistik bezieht sich auf die Praxis der Aufteilung von Personen in einer Studie in "Blöcke" auf der Grundlage eines bestimmten Wertes einer Störvariable, um den Effekt der Störvariable zu eliminieren.

Angenommen, die Forscher wollen herausfinden, wie sich eine neue Diät auf die Gewichtsabnahme auswirkt. Die unabhängige Variable ist die neue Diät und die abhängige Variable ist die Höhe des Gewichtsverlusts.

Eine Störvariable, die wahrscheinlich zu Abweichungen bei der Gewichtsabnahme führt, ist jedoch das Geschlecht. Es ist wahrscheinlich, dass das Geschlecht einer Person die Menge an Gewicht, die sie verliert, beeinflusst, unabhängig davon, ob die neue Diät funktioniert oder nicht.

Eine Möglichkeit, mit diesem Problem umzugehen, besteht darin, die Personen in einen von zwei Blöcken einzuteilen:

• Männlich
• Frau

Dann würden wir innerhalb jedes Blocks die Personen nach dem Zufallsprinzip einer von zwei Behandlungen zuordnen:

• Eine neue Diät
• Eine Standard-Diät

Auf diese Weise wäre die Variation innerhalb jedes Blocks viel geringer als die Variation zwischen allen Individuen, und wir wären in der Lage, ein besseres Verständnis dafür zu gewinnen, wie sich die neue Diät auf die Gewichtsabnahme auswirkt, während das Geschlecht kontrolliert wird.

3. Abgleich

Ein Matched Pairs Design (dt. ~ paarweise Zuordnung) ist eine Art von Versuchsplan, bei dem wir Individuen auf der Grundlage von Werten potenzieller Störvariablen "abgleichen".

Angenommen, Forscher wollen wissen, wie sich eine neue Diät im Vergleich zu einer Standarddiät auf den Gewichtsverlust auswirkt. Zwei potenzielle Störvariablen in dieser Situation sind Alter und Geschlecht.

Um dies zu berücksichtigen, rekrutieren die Forscher 100 Probanden und gruppieren die Probanden dann in 50 Paare, basierend auf ihrem Alter und Geschlecht. Zum Beispiel:

• Ein 25-jähriger Mann wird mit einem anderen 25-jährigen Mann gepaart, da sie in Bezug auf Alter und Geschlecht "übereinstimmen".
• Eine 30-jährige Frau wird mit einer anderen 30-jährigen Frau gepaart, da sie ebenfalls in Bezug auf Alter und Geschlecht übereinstimmen, und so weiter.

Dann wird innerhalb jedes Paares eine Testperson nach dem Zufallsprinzip der neuen Diät für 30 Tage und die andere Testperson der Standarddiät für 30 Tage zugewiesen.

Am Ende der 30 Tage messen die Forscher den Gesamtgewichtsverlust für jede Versuchsperson.

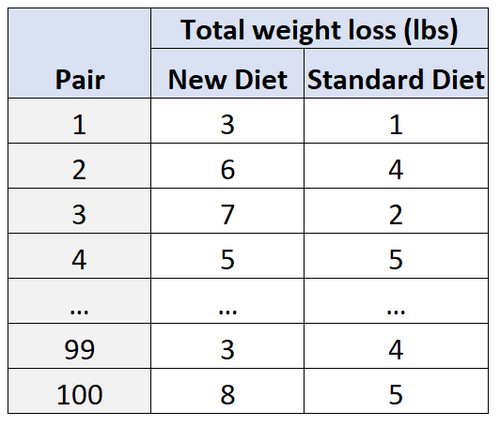
Durch die Verwendung dieser Art von Design können die Forscher sicher sein, dass etwaige Unterschiede bei der Gewichtsabnahme auf die Art der verwendeten Diät und nicht auf die Störvariablen Alter und Geschlecht zurückgeführt werden können.

Diese Art von Design hat ein paar Nachteile, darunter:

1. Verlust von zwei Probanden, wenn einer ausscheidet. Wenn ein Proband aus der Studie ausscheidet, verliert man tatsächlich zwei Probanden, da man kein vollständiges Paar mehr hat.

2. Zeitaufwendig, um Übereinstimmungen zu finden. Es kann recht zeitaufwendig sein, Personen zu finden, die in bestimmten Variablen wie Geschlecht und Alter übereinstimmen.

3. Es ist unmöglich, Personen perfekt zuzuordnen. Egal wie sehr man sich bemüht, es wird immer eine gewisse Variation innerhalb der Probanden eines Paares geben.

Wenn eine Studie jedoch über die nötigen Ressourcen verfügt, um dieses Design umzusetzen, kann es sehr effektiv sein, um die Auswirkungen von Störvariablen zu eliminieren.