So berechnen Sie das Quotenverhältnis und das relative Risiko in Excel

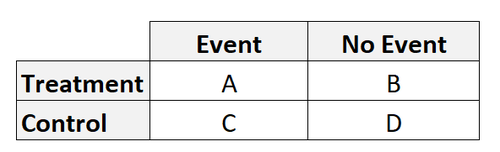
Wir verwenden häufig das Quotenverhältnis und das relative Risiko, wenn wir eine Analyse an einer 2x2-Tabelle durchführen, die das folgende Format annimmt:

Das Quotenverhältnis gibt uns das Verhältnis der Wahrscheinlichkeit eines Ereignisses in einer Behandlungsgruppe zu der Wahrscheinlichkeit eines Ereignisses in einer Kontrollgruppe an. Es wird berechnet als:

Quotenverhältnis = (A*D) / (B*C)

Das relative Risiko gibt uns das Verhältnis der Eintrittswahrscheinlichkeit eines Ereignisses in einer Behandlungsgruppe zur Eintrittswahrscheinlichkeit eines Ereignisses in einer Kontrollgruppe an. Es wird berechnet als:

Relatives Risiko = [A/(A+B)] / [C/(C+D)]

In diesem Tutorial wird erklärt, wie Sie Quotenverhältniss und das relative Risiko in Excel berechnen.

So berechnen Sie das Quotenverhältnis und das relative Risiko

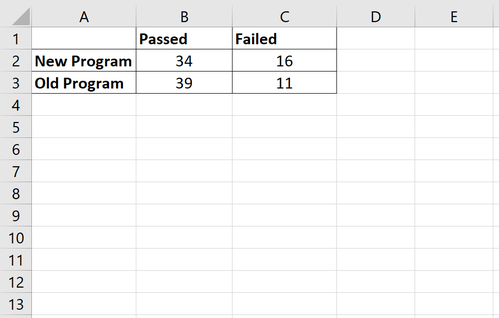
Angenommen, 50 Basketballspieler verwenden ein neues Trainingsprogramm und 50 Spieler verwenden ein altes Trainingsprogramm. Am Ende des Programms testen wir jeden Spieler, um zu sehen, ob er einen bestimmten Fähigkeitstest besteht. Die folgende Tabelle zeigt die Anzahl der Spieler, die bestanden und nicht bestanden haben, basierend auf dem von ihnen verwendeten Programm:

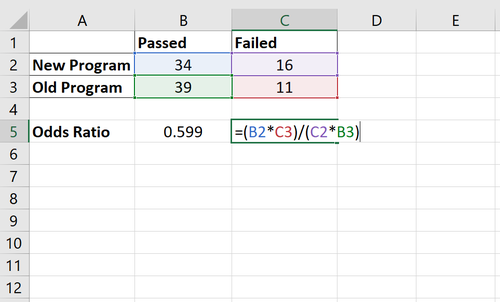
Das Quotenverhältnis wird berechnet als (34*11) / (16*39) = 0,599

Wir würden dies so interpretieren, dass die Chance, dass ein Spieler den Test mit dem neuen Programm besteht, nur das 0,599-fache der Chance beträgt, dass ein Spieler den Test mit dem alten Programm besteht. Mit anderen Worten, die Chance, dass ein Spieler den Test besteht, wird durch die Verwendung des neuen Programms tatsächlich um 40,1% gesenkt.

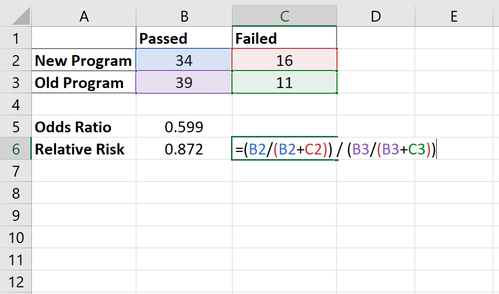
Das relative Risiko wird berechnet als [34/(34+16)] / [39/(39+11)] = 0,872

Wir würden dies so interpretieren, dass das Verhältnis der Wahrscheinlichkeit, dass ein Spieler den Test mit dem neuen Programm im Vergleich zum alten Programm besteht, 0,872 beträgt. Da dieser Wert kleiner als 1 ist, bedeutet dies, dass die Wahrscheinlichkeit des Bestehens unter dem neuen Programm im Vergleich zum alten Programm tatsächlich geringer ist.

Wir könnten dies auch sehen, indem wir die Wahrscheinlichkeit, mit der ein Spieler unter jedem Programm passt, direkt berechnen:

Wahrscheinlichkeit des Bestehens im neuen Programm = 34 / 50 = 68%

Wahrscheinlichkeit des Bestehens im alten Programm = 39 / 50 = 78%

So berechnen Sie Konfidenzintervalle

Sobald wir das Quotenverhältnis und das relative Risiko berechnet haben, könnten wir auch daran interessiert sein, Konfidenzintervalle für diese beiden Metriken zu berechnen.

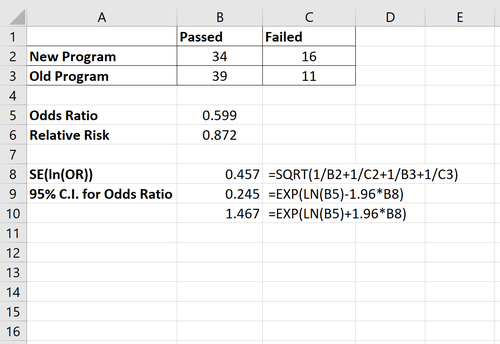
Ein 95-%-Konfidenzintervall für die Quotenverhältnis kann mit der folgenden Formel berechnet werden:

95%-Konfidenzintervall für das Quotenverhältnis (engl. Odds Ratio, kurz OR) = [e^(ln(OR) – 1,96*SE(ln(OR))), e^(ln(OR) – 1,96*SE(ln(OR)))]

wobei SE(ln(OR)) =√1/A + 1/B + 1/C + 1/D

Das 95%-Konfidenzintervall für das Quotenverhältnis ergibt sich zu (0,245, 1,467). Das Bild unten zeigt die Formel, die wir zur Berechnung dieses Konfidenzintervalls verwendet haben:

(Die Formeln im untenstehenden Bild wurden mit einer englischsprachen Excel-Version erstellt. Für die deutschen Formeln siehe z.B. hier)

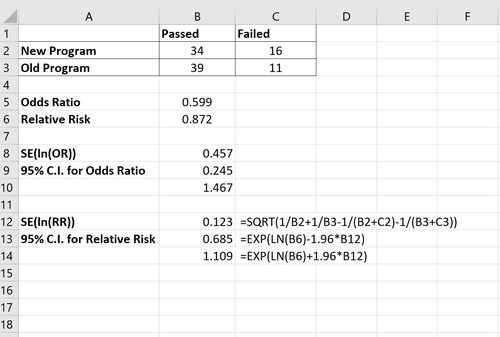
Ein 95%-Konfidenzintervall für das relative Risiko lässt sich nach folgender Formel berechnen:

95%-Konfidenzintervall für relatives Risiko = exp(ln(RR) – 1,96*SE(ln(RR))) to exp(ln(RR) – 1,96*SE(ln(RR)))

wobei SE(ln(RR)) =√1/A + 1/C – 1/(A+B) – 1/(C+D)

Das 95%-Konfidenzintervall für das relative Risiko ist (0,685; 1,109). Das Bild unten zeigt die Formel, die wir zur Berechnung dieses Konfidenzintervalls verwendet haben:

(Die Formeln im untenstehenden Bild wurden mit einer englischsprachen Excel-Version erstellt. Für die deutschen Formeln siehe z.B. hier)