Erstellen und Interpretieren eines Q-Q-Diagramms in R

Ein Q-Q-Plot, kurz für Quantil-Quantil-Diagramm, ist eine Art von Plot, mit dem wir bestimmen können, ob ein Datensatz möglicherweise aus einer theoretischen Verteilung stammt oder nicht.

Bei vielen statistischen Tests wird davon ausgegangen, dass ein Datensatz einer Normalverteilung folgt, und häufig wird ein Q-Q-Diagramm verwendet, um zu bewerten, ob diese Annahme erfüllt ist oder nicht.

Obwohl ein Q-Q-Diagramm kein formaler statistischer Test ist, bietet es eine einfache Möglichkeit, visuell zu überprüfen, ob ein Datensatz einer Normalverteilung folgt und wenn nicht, wie diese Annahme verletzt wird und welche Datenpunkte möglicherweise diese Verletzung verursachen.

Wir können ein Q-Q-Diagramm erstellen, indem wir zwei Datensätze von Quantilen gegeneinander auftragen. Wenn beide Quantilmengen aus derselben Verteilung stammen, sollten die Punkte auf dem Plot ungefähr eine gerade diagonale Linie bilden.

Q-Q-Diagramme identifizieren die Quantile in Ihren Probendaten und zeichnen sie gegen die Quantile einer theoretischen Verteilung. In den meisten Fällen wird die Normalverteilung verwendet, aber für jede theoretische Verteilung kann tatsächlich ein Q-Q-Diagramm erstellt werden.

Wenn die Datenpunkte in einem Q-Q-Diagramm entlang einer geraden diagonalen Linie liegen, folgt der Datensatz wahrscheinlich einer Normalverteilung.

So erstellen Sie ein Q-Q-Diagramm in R

Mithilfe der integrierten Funktion qqnorm() können wir auf einfache Weise ein Q-Q-Diagramm erstellen, um zu überprüfen, ob ein Datensatz einer Normalverteilung folgt.

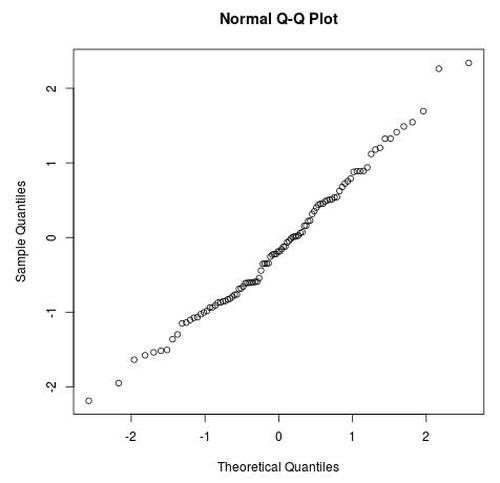
Der folgende Code generiert beispielsweise einen Vektor mit 100 Zufallswerten, die einer Normalverteilung folgen, und erstellt ein Q-Q-Diagramm für diesen Datensatz, um zu überprüfen, ob er tatsächlich einer Normalverteilung folgt:

#Machen Sie dieses Beispiel reproduzierbar
set.seed(11)

#Generieren Sie einen Vektor mit 100 Werten, der einer Normalverteilung folgt
data <- rnorm(100)
#Erstellen Sie ein Q-Q-Diagramm, um diesen Datensatz mit einer theoretischen Normalverteilung zu vergleichen
qqnorm(data)

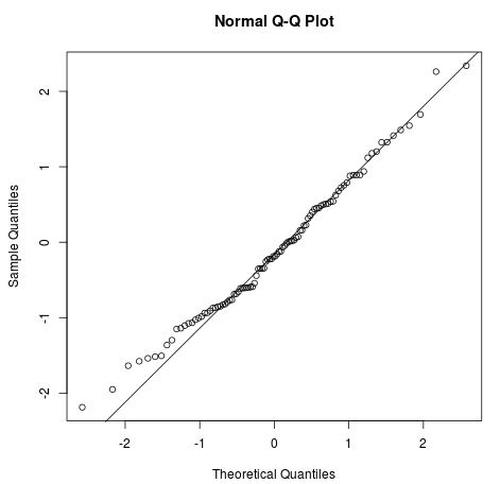
Um noch einfacher zu erkennen, ob die Daten entlang einer geraden Linie liegen, können wir die Funktion qqline() verwenden:

# Q-Q-Plot erstellen
qqnorm(data)
#Gerade diagonale Linie zum Plot hinzufügen
qqline(data)

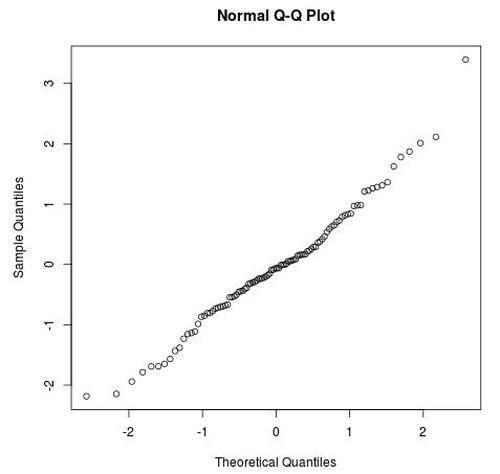
Wir können sehen, dass die Datenpunkte in der Nähe der Schwänze nicht genau entlang der geraden Linie liegen, aber zum größten Teil scheinen diese Beispieldaten normal verteilt zu sein (wie es sein sollte, da wir R angewiesen haben, die Daten aus einer Normalverteilung zu generieren ).

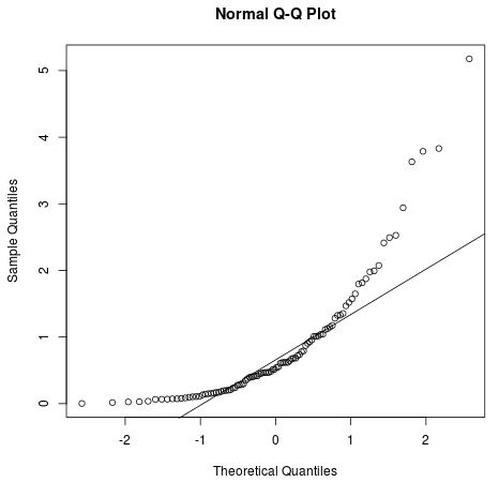
Betrachten Sie stattdessen den folgenden Code, der einen Vektor mit 100 Zufallswerten generiert, die einer Gammaverteilung folgen, und ein Q-Q-Diagramm für diese Daten erstellt, um zu überprüfen, ob sie einer Normalverteilung folgen:

#Machen Sie dieses Beispiel reproduzierbar
set.seed (11)

#Generieren Sie einen Vektor mit 100 Werten, der einer Gammaverteilung folgt
data <- rgamma(100, 1)

#Erstellen Sie ein Q-Q-Diagramm, um diesen Datensatz mit einer theoretischen Normalverteilung zu vergleichen
qqnorm(data)
qqline(data)

Wir können die deutliche Abweichung von der geraden Linie in diesem Q-Q-Diagramm sehen, was darauf hinweist, dass dieser Datensatz wahrscheinlich keiner Normalverteilung folgt.

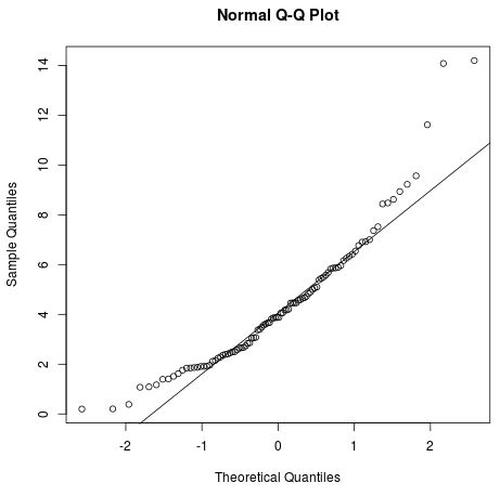
Stellen Sie sich einen weiteren Codeabschnitt vor, der einen Vektor mit 100 Zufallswerten generiert, die einer Chi-Quadrat-Verteilung mit 5 Freiheitsgraden folgen, und ein Q-Q-Diagramm für diese Daten erstellt, um zu überprüfen, ob sie einer Normalverteilung folgen:

#Machen Sie dieses Beispiel reproduzierbar
set.seed(11)

#Generieren Sie einen Vektor mit 100 Werten, der einer Chi-Quadrat-Verteilung folgt
data <- rchisq(100, 5)
#Erstellen Sie ein Q-Q-Diagramm, um diesen Datensatz mit einer theoretischen Normalverteilung zu vergleichen
qqnorm(data)
qqline(data)

Wieder einmal können wir sehen, dass dieser Datensatz keiner Normalverteilung zu folgen scheint, insbesondere in der Nähe der Schwänze.

Ändern der Ästhetik eines Q-Q-Diagramms in R

Wir können einige der Ästhetiken des Q-Q-Diagramms in R ändern, einschließlich Titel, Achsenbeschriftungen, Datenpunktfarben, Linienfarbe und Linienbreite.

Der folgende Code ändert die Titel, Achsenbeschriftungen und Farben der Punkte im Diagramm:

#Machen Sie dieses Beispiel reproduzierbar
set.seed(11)

#Generieren Sie einen Vektor mit 100 Werten, der einer Normalverteilung folgt
data <- rnorm(100)
#Q-Q-Plot erstellen
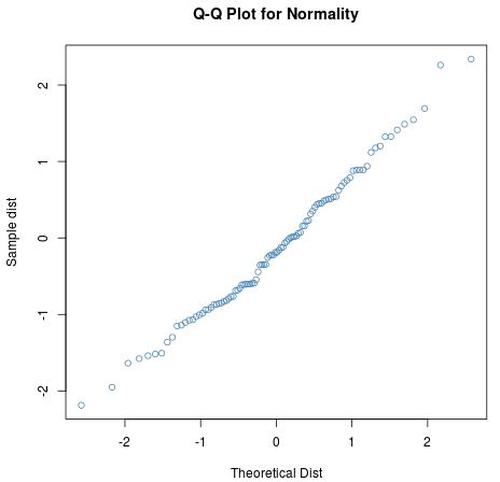
qqnorm(data, main = 'Q-Q Plot for Normality', xlab = 'Theoretical Dist',
       ylab = 'Sample dist', col = 'steelblue')

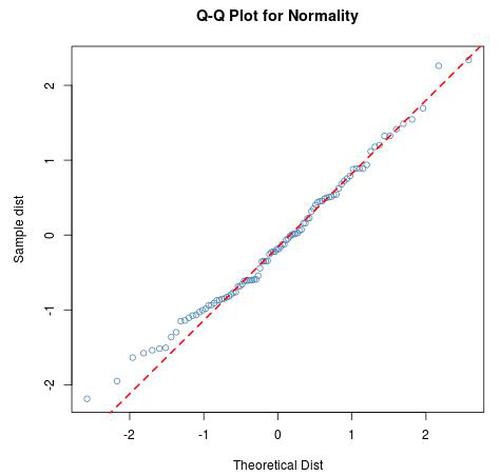
Als nächstes fügt der folgende Code dem Diagramm eine gerade diagonale Linie mit einer roten Farbe, einer Linienbreite von 2 (lwd = 2, Standard ist 1) und einer gestrichelten Linie (lty = 2, Standard ist 1) hinzu:

qqline(data, col = 'red', lwd = 2, lty = 2)

Technische Hinweise

Beachten Sie, dass ein Q-Q-Plot lediglich eine Möglichkeit ist, visuell zu überprüfen, ob ein Datensatz einer theoretischen Verteilung folgt. Um formal zu testen, ob ein Datensatz einer bestimmten Verteilung folgt oder nicht, können die folgenden Tests durchgeführt werden (vorausgesetzt, Sie vergleichen Ihren Datensatz mit einer Normalverteilung):

Anderson-Darling-Test