So berechnen Sie den Phi-Koeffizienten in R

Ein Phi-Koeffizient (manchmal auch als mittlerer quadratischer Kontingenzkoeffizient bezeichnet ) ist ein Maß für die Assoziation zwischen zwei binären Variablen.

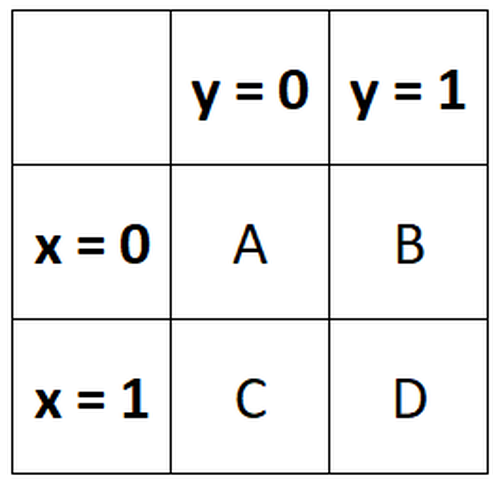
Für eine gegebene 2 × 2-Tabelle für zwei Zufallsvariablen x und y :

Der Phi-Koeffizient kann berechnet werden als:

Φ = (AD-BC) / √ (A + B) (C + D) (A + C) (B + D)

Beispiel: Berechnung eines Phi-Koeffizienten in R

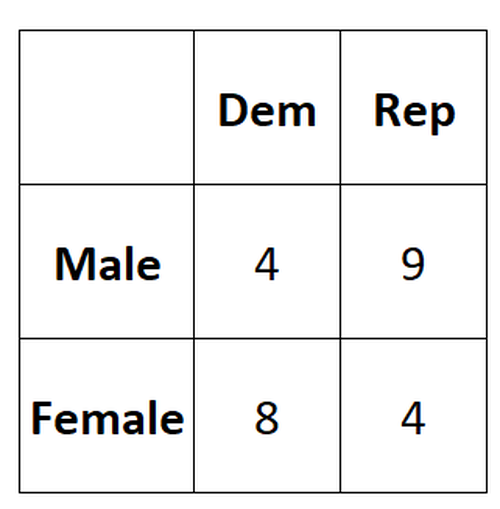
Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz der politischen Partei zusammenhängt oder nicht, also nehmen wir eine einfache Zufallsstichprobe von 25 Wählern und befragen sie nach ihrer Präferenz für die politische Partei.

Die folgende Tabelle zeigt die Ergebnisse der Umfrage:

Wir können den folgenden Code verwenden, um diese Daten in eine 2 × 2-Matrix in R einzugeben:

#2x2-Tabelle erstellen
data = matrix(c(4, 8, 9, 4), nrow = 2)

#Datensatz anzeigen
data

     [,1] [,2]
[1,]    4    9
[2,]    8    4

Wir können dann die Funktion phi() aus dem psych-Paket verwenden, um den Phi-Koeffizienten zwischen den beiden Variablen zu berechnen:

#psych-Paket laden
library(psych)

#Phi-Koeffizient berechnen
phi(data)

[1] -0.36

Der Phi-Koeffizient beträgt -0,36.

Beachten Sie, dass die Phi-Funktion standardmäßig auf 2 Stellen gerundet wird. Sie können jedoch festlegen, dass die Funktion auf so viele Stellen gerundet werden soll, wie Sie möchten:

#Phi-Koeffizient berechnen und auf 6 Stellen runden
phi(data, digits = 6)

[1] -0.358974

Wie man einen Phi-Koeffizienten interpretiert

Ähnlich wie bei einem Pearson-Korrelationskoeffizienten nimmt ein Phi-Koeffizient Werte zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative Beziehung zwischen den beiden Variablen an.
• 0 zeigt keine Zuordnung zwischen den beiden Variablen an.
• 1 zeigt eine vollkommen positive Beziehung zwischen den beiden Variablen an.

Im Allgemeinen ist die Beziehung zwischen den beiden Variablen umso stärker, je weiter ein Phi-Koeffizient von Null entfernt ist.

Mit anderen Worten, je weiter ein Phi-Koeffizient von Null entfernt ist, desto mehr Beweise gibt es für eine Art systematisches Muster zwischen den beiden Variablen.

Zusätzliche Ressourcen

Eine Einführung in den Phi-Koeffizienten
Phi-Koeffizientenrechner