Permutationstests in R - so geht's

Ein Permutationstest (manchmal auch als Randomisierungstest bezeichnet) ist eine Möglichkeit, einen Unterschied in den Ergebnissen zwischen verschiedenen Behandlungsgruppen festzustellen.

In diesem Tutorial wird anhand eines Beispiels in R erläutert, wie ein Permutationstest durchgeführt wird.

Ein Permutationstestbeispiel

Die Forscher möchten wissen, ob Trainingsprogramm A oder Trainingsprogramm B Basketballspielern hilft, innerhalb eines Monats mehr Gewicht zuzunehmen. Um die Unterschiede zwischen den Trainingsprogrammen zu testen, rekrutieren die Forscher 100 Spieler und weisen zufällig 50 für die Verwendung von Programm A und 50 für die Verwendung von Programm B für einen Monat zu.

#Seed setzen, um dieses Beispiel replizierbar zu machen
set.seed(0)

#Erstellen Sie ein Dataframe, das das Trainingsprogramm und die daraus resultierende Gewichtszunahme für 100 Spieler zeigt
data <- data.frame(treatment = rep(c('A', 'B'), each = 50))
data$weight_gain <- ifelse(data$treatment == 'A', rnorm(50, 10, 2), rnorm(50, 12, 2))

# Die ersten 6 Zeilen und die letzten 6 Zeilen des Dataframes anzeigen
head(data); tail(data)

#  treatment weight_gain
#1         A   12.525909
#2         A    9.347533
#3         A   12.659599
#4         A   12.544859
#5         A   10.829283
#6         A    6.920100

#    treatment weight_gain
#95          B    13.19252
#96          B    12.23944
#97          B    11.43565
#98          B    14.91198
#99          B    12.45804
#100         B    13.99309

Als nächstes können wir den Unterschied in der mittleren Gewichtszunahme zwischen den beiden Programmen finden:

#Mittlere Gewichtszunahme für Spieler in Programm A finden
mean_A <- mean(data$weight_gain[data$treatment == 'A'])

#Mittlere Gewichtszunahme für Spieler in Programm B finden
mean_B <- mean(data$weight_gain[data$treatment == 'B'])

# Unterschied zwischen mittleren Gewichtszunahmen der Programme finden
mean_B - mean_A

#[1] 1.99495

Wir können sehen, dass die Spieler in Programm B durchschnittlich 1,99 Pfund mehr zugenommen haben als die Spieler in Programm A.

Die Idee hinter dem Permutationstest ist nun, dass wir die beobachteten Daten „mischen“ oder permutieren können, indem wir jeder Beobachtung aus der Menge der tatsächlich beobachteten Ergebnisse unterschiedliche Ergebniswerte zuweisen.

Wenn wir die Ergebniswerte während des Tests permutieren, können wir alle möglichen alternativen Behandlungszuordnungen sehen, die wir hätten haben können. Auf diese Weise können wir sehen, wo der mittlere Unterschied in unseren beobachteten Daten im Verhältnis zu allen mittleren Unterschieden, die wir hätten sehen können, abfällt.

Ein Permutationstest erfordert, dass wir alle möglichen Permutationen der Daten sehen, aber dies kann eine große Anzahl von Permutationen sein, wenn die Daten sogar etwas groß sind.

Somit können wir einen ungefähren Permutationstest durchführen, indem wir einfach eine große Anzahl von Resamples durchführen. Dies sollte es uns ermöglichen, die tatsächliche Permutationsverteilung zu approximieren.

Um eine einzelne Permutation der Daten zu erhalten, können wir von den beobachteten Daten eine Stichprobe ohne Zurücklegen ziehen und die mittlere Differenz zwischen den beiden Programmen erneut berechnen:

#Stichprobe aus den ursprünglichen Datenbehandlungswerten ohne Zurücklegen
samp <- sample(data$treatment, length(data$treatment), replace = FALSE)

#Erstellen Sie einen neues Dataframe mit den ursprünglichen Behandlungen ('A' und 'B') randomisiert
data_permutation <- data
data_permutation$treatment <- samp

#Sehen Sie sich die ersten 6 und letzten 6 Zeilen dieses neuen permutierten Dataframes an
head(data_permutation); tail(data_permutation)

#  treatment weight_gain
#1         B   12.525909
#2         A    9.347533
#3         A   12.659599
#4         B   12.544859
#5         A   10.829283
#6         A    6.920100

#    treatment weight_gain
#95          A    13.19252
#96          B    12.23944
#97          A    11.43565
#98          A    14.91198
#99          A    12.45804
#100         A    13.99309

Beachten Sie, dass alle weight_gain-Werte gleich geblieben sind, die Behandlungen jedoch jetzt verwechselt sind. Dieses neue Dataframe repräsentiert eine permutierte Version unseres ursprünglichen Dataframes.

Jetzt können wir den Unterschied zwischen den beiden Trainingsprogrammen anhand dieser permutierten Daten feststellen:

#Mittlere Gewichtszunahme für Spieler in Programm A finden
mean_A <- mean(data_permutation$weight_gain[data_permutation$treatment == 'A'])

#Mittlere Gewichtszunahme für Spieler in Programm B finden
mean_B <- mean(data_permutation$weight_gain[data_permutation$treatment == 'B'])

#Unterschied zwischen mittleren Gewichtszunahmen der Programme finden
mean_B - mean_A

#[1] -0.4353178

Wenn wir diesen Vorgang viele Male wiederholen, können wir unsere ungefähre Permutationsverteilung erstellen, die die Stichprobenverteilung für die mittlere Differenz darstellt. Wir können eine einfache for-Schleife in R verwenden, um diesen Permutationsprozess 3.000 Mal auszuführen und die mittleren Differenzen an einen Vektor auszugeben:

#Erstelle einen leeren Vektor
diff_vector <- numeric(0)

#Erstellen Sie 3.000 Permutationen des ursprünglichen Dataframes und ermitteln Sie den mittleren Unterschied
#zwischen den beiden Programmen in jeder Permutation, dann schreiben Sie diese mittlere Differenz
#in einen Vektore
for(i in 1:3000) {
samp <- sample(data$treatment, length(data$treatment), replace = FALSE)

data_permutation <- data
data_permutation$treatment <- samp

mean_A <- mean(data_permutation$weight_gain[data_permutation$treatment == 'A'])
mean_B <- mean(data_permutation$weight_gain[data_permutation$treatment == 'B'])

#Differenz zwischen mittleren Gewichtszunahmen des Pogramms finden
find difference between mean weight gains of the programs
diff_vector[i] <- mean_B - mean_A

}

#Die ersten 6 Mittlwert-DIfferenzen anzeigen
head(diff_vector)

#[1] -0.4353178 0.2503843 -0.5839568 -0.1733017 0.1372405 0.6878647

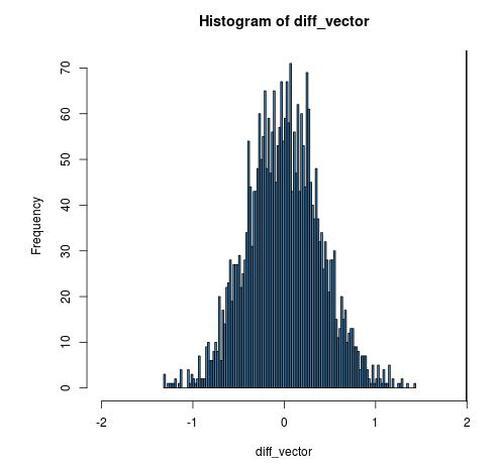
Als nächstes können wir ein Histogramm erstellen, um diese Verteilung der mittleren Differenzen anzuzeigen und eine vertikale Linie bei unserer tatsächlich beobachteten mittleren Differenz von 1,99495 zu zeichnen.

hist(diff_vector, xlim=c(-2, 2), col = "steelblue", breaks = 100)
abline(v = 1.99495, col = "black", lwd = 2)

Unser beobachteter mittlerer Unterschied in der Gewichtszunahme erscheint im Hinblick auf die Verteilung möglicher mittlerer Unterschiede ziemlich extrem, wenn die Gewichtszunahme tatsächlich unabhängig von der Behandlung war.

Wir können diese Verteilung verwenden, um einen p-Wert für unsere beobachtete mittlere Differenz zu erhalten, indem wir zählen, wie viele permutierte mittlere Differenzen größer sind als die, die wir in unseren tatsächlichen Daten beobachtet haben, und dann durch die Anzahl der permutierten Verteilungen dividieren, die in diesem Fall 3.000 beträgt:

#einseitiger Test
sum(diff_vector > 1.99495)/3000

[1] 0

#zweiseitiger Test
sum(abs(diff_vector) > 1.99495)/3000

[1] 0

Unabhängig davon, ob wir einen einseitigen oder einen zweiseitigen Test durchführen, ist unser p-Wert in beiden Fällen Null. Dies weist darauf hin, dass unser Unterschied wahrscheinlich nicht zufällig ist, wenn die Gewichtszunahme tatsächlich unabhängig von der Behandlung war.

Permutationstest mit der coin-Bibliothek

Anstatt einen Permutationstest durch Schreiben unseres eigenen Codes durchzuführen, könnten wir einfach die coin-Bibliothek in R verwenden.

#coin-Bibliothek laden
library(coin)

#einseitiger Test
independence_test(data$weight_gain ~ data$treatment, alternative = "less")

#   Asymptotic General Independence Test
#
#data:  data$weight_gain by data$treatment (A, B)
#Z = -4.9134, p-value = 4.475e-07
#alternative hypothesis: less

#zweiseitiger Test
independence_test(data$weight_gain ~ data$treatment) 

#   Asymptotic General Independence Test
#
#data:  data$weight_gain by data$treatment (A, B)
#Z = -4.9134, p-value = 8.949e-07
#alternative hypothesis: two.sided

Aus den Testergebnissen können wir ersehen, dass unsere ungefähre Permutationsverteilung dieselbe Inferenz und einen nahezu identischen p-Wert wie die coin-Bibliothek lieferte.