Pearson-Korrelationskoeffizient

Der Pearson-Korrelationskoeffizient (auch als „Produkt-Moment-Korrelationskoeffizient“ bekannt) ist ein Maß für die lineare Assoziation zwischen zwei Variablen X und Y. Er hat einen Wert zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 zeigt keine lineare Korrelation zwischen zwei Variablen an
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Die Formel zum Ermitteln des Pearson-Korrelationskoeffizienten

Die Formel zum Ermitteln des mit r bezeichneten Pearson-Korrelationskoeffizienten für eine Datenstichprobe lautet (über Wikipedia):

Sie werden diese Formel wahrscheinlich nie von Hand berechnen müssen, da Sie Software verwenden können, um dies für Sie zu tun. Es ist jedoch hilfreich, anhand eines Beispiels zu verstehen, was genau diese Formel bewirkt.

Angenommen, wir haben den folgenden Datensatz:

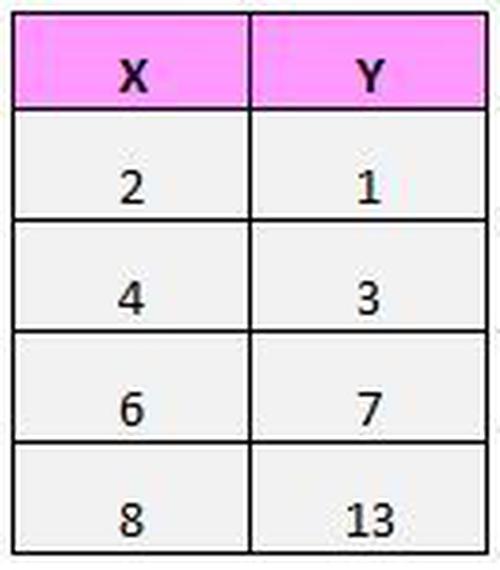Wenn wir diese (X, Y) Paare in einem Streudiagramm darstellen würden, würde dies folgendermaßen aussehen:

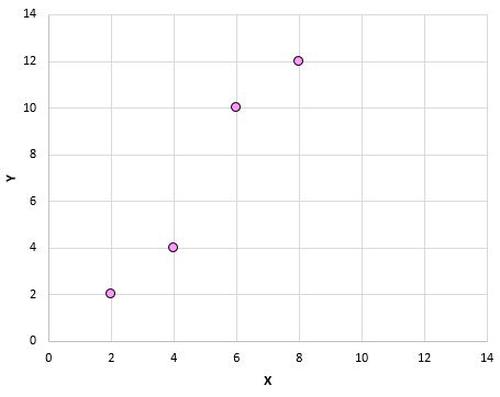Wenn wir uns dieses Streudiagramm ansehen, können wir erkennen, dass es eine positive Assoziation zwischen den Variablen X und Y gibt: Wenn X zunimmt, nimmt auch Y tendenziell zu. Um jedoch genau zu quantifizieren, wie positiv diese beiden Variablen assoziiert sind, müssen wir den Pearson-Korrelationskoeffizienten ermitteln.

Konzentrieren wir uns nur auf den Zähler der Formel:

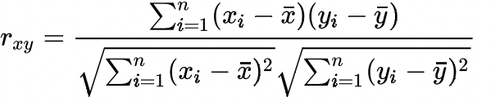Für jedes (X, Y) Paar in unserem Datensatz müssen wir die Differenz zwischen dem x-Wert und dem mittleren x-Wert, die Differenz zwischen dem y-Wert und dem mittleren y-Wert ermitteln und diese beiden Zahlen dann miteinander multiplizieren.

Zum Beispiel ist unser erstes (X, Y) Paar (2, 2). Der mittlere x-Wert in diesem Datensatz beträgt 5 und der mittlere y-Wert in diesem Datensatz beträgt 7. Die Differenz zwischen dem x-Wert in diesem Paar und dem mittleren x-Wert beträgt also 2 – 5 = -3. Die Differenz zwischen dem y-Wert in diesem Paar und dem mittleren y-Wert beträgt 2 – 7 = -5. Wenn wir dann diese beiden Zahlen miteinander multiplizieren, erhalten wir -3 * -5 = 15.

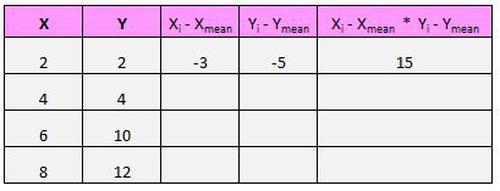Hier ist ein visueller Blick auf das, was wir gerade gemacht haben:

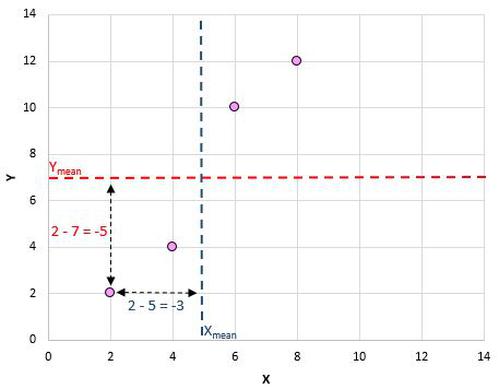Als nächstes müssen wir dies nur für jedes einzelne Paar tun:

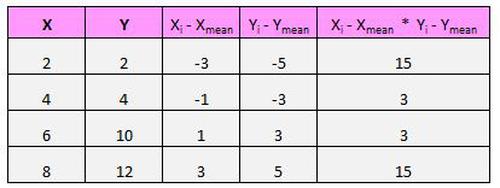
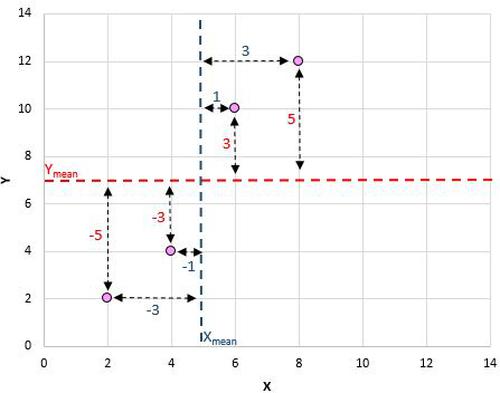Der letzte Schritt, um den Zähler der Formel zu erhalten, besteht darin, einfach alle diese Werte zu addieren:

15 + 3 + 3 + 15 = 36

Als nächstes sagt uns der Nenner der Formel, wir sollen die Summe aller quadratischen Differenzen für x und y ermitteln, dann diese beiden Zahlen miteinander multiplizieren und dann die Quadratwurzel ziehen:

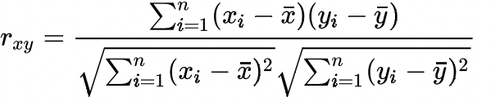Zuerst finden wir die Summe der quadratischen Differenzen für x und y:

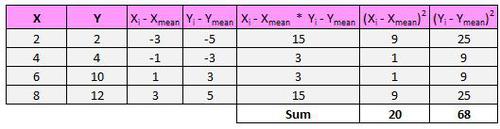Zuletzt ziehen wir die Quadratwurzel: √1.360 = 36,88

Wir haben also festgestellt, dass der Zähler der Formel 36 und der Nenner 36,88 ist. Dies bedeutet, dass unser Pearson-Korrelationskoeffizient r = 36 / 36,88 = 0,976 ist

Diese Zahl liegt nahe bei 1, was darauf hinweist, dass zwischen unseren Variablen X und Y eine starke positive lineare Beziehung besteht. Dies bestätigt die Beziehung, die wir im Streudiagramm gesehen haben.

Korrelationen visualisieren

Denken Sie daran, dass ein Pearson-Korrelationskoeffizient die Art der linearen Beziehung (positiv, negativ, keine) zwischen zwei Variablen sowie die Stärke dieser Beziehung (schwach, moderat, stark) angibt.

Wenn wir ein Streudiagramm von zwei Variablen erstellen, können wir die tatsächliche Beziehung zwischen zwei Variablen sehen. Hier sind die vielen verschiedenen Arten von linearen Beziehungen, die wir möglicherweise sehen (siehe auch Streudiagramm):

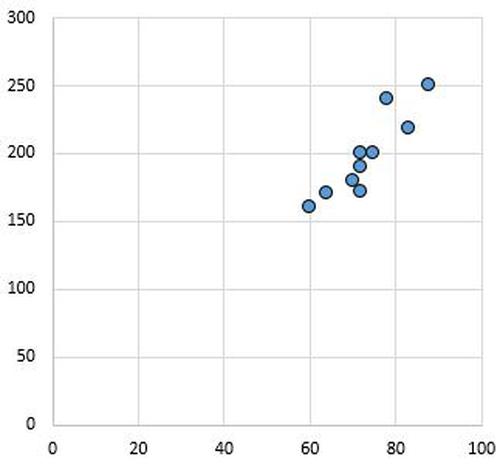Starke, positive Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt auch die Variable auf der y-Achse zu. Die Punkte sind eng zusammengepackt, was auf eine starke Beziehung hinweist.

Pearson-Korrelationskoeffizient: 0,94

Schwache, positive Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt auch die Variable auf der y-Achse zu. Die Punkte sind ziemlich verteilt, was auf eine schwache Beziehung hinweist.

Pearson-Korrelationskoeffizient: 0,44

Keine Beziehung: Es gibt keine eindeutige Beziehung (positiv oder negativ) zwischen den Variablen.

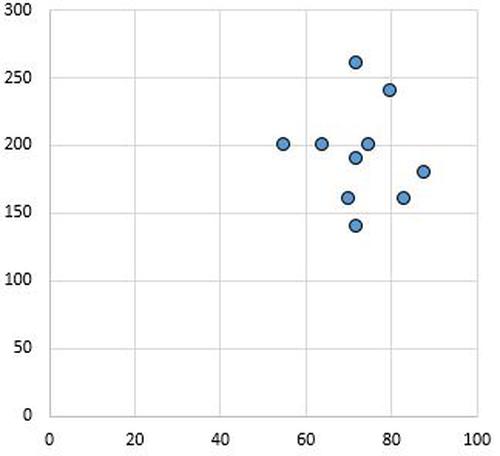Pearson-Korrelationskoeffizient: 0,03

Starke, negative Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt die Variable auf der y-Achse ab. Die Punkte sind eng zusammengepackt, was auf eine starke Beziehung hinweist.

Pearson-Korrelationskoeffizient: -0,87

Schwache, negative Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt die Variable auf der y-Achse ab. Die Punkte sind ziemlich verteilt, was auf eine schwache Beziehung hinweist.

Pearson-Korrelationskoeffizient: –0,46

Testen auf Signifikanz eines Pearson-Korrelationskoeffizienten

Testen auf Signifikanz eines Pearson-Korrelationskoeffizienten
Wenn wir den Pearson-Korrelationskoeffizienten für einen Datensatz finden, arbeiten wir häufig mit einer Stichprobe von Daten, die aus einer größeren Population stammen. Dies bedeutet, dass es möglich ist, eine Korrelation ungleich Null für zwei Variablen zu finden, auch wenn diese in der Gesamtbevölkerung tatsächlich nicht korreliert sind.

Angenommen, wir erstellen für jeden Datenpunkt in der gesamten Grundgesamtheit ein Streudiagramm für die Variablen X und Y, und es sieht folgendermaßen aus:

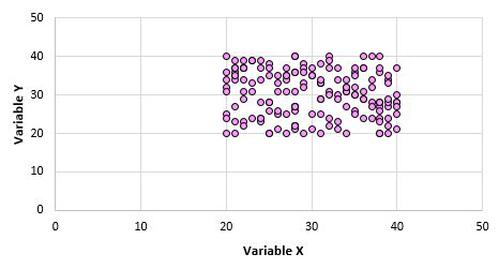Diese beiden Variablen sind eindeutig nicht korreliert. Es ist jedoch möglich, dass wir bei einer Stichprobe von 10 Punkten aus der Bevölkerung die folgenden Punkte auswählen:

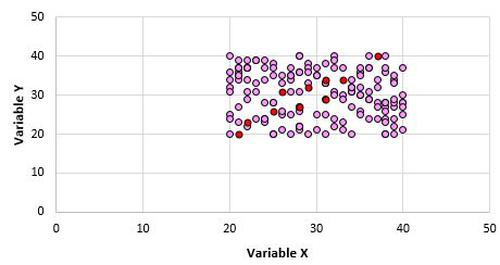Wir können feststellen, dass der Pearson-Korrelationskoeffizient für diese Stichprobe von Punkten 0,93 beträgt, was auf eine starke positive Korrelation hinweist, obwohl die Populationskorrelation Null ist.

Um zu testen, ob eine Korrelation zwischen zwei Variablen statistisch signifikant ist oder nicht, können wir die folgende Teststatistik finden:

Teststatistik T = r * √(n-2) / (1-r²)

Dabei ist n die Anzahl der Paare in unserer Stichprobe, r der Pearson-Korrelationskoeffizient und die Teststatistik T folgt einer t-Verteilung mit n-2 Freiheitsgraden.

Lassen Sie uns ein Beispiel durchgehen, wie die Signifikanz eines Pearson-Korrelationskoeffizienten getestet wird.

Beispiel

Der folgende Datensatz zeigt die Größe und das Gewicht von 12 Personen:

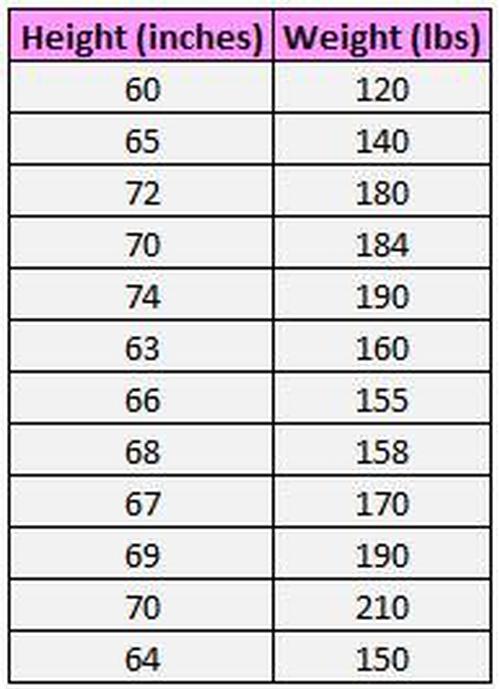Das Streudiagramm unten zeigt den Wert dieser beiden Variablen:

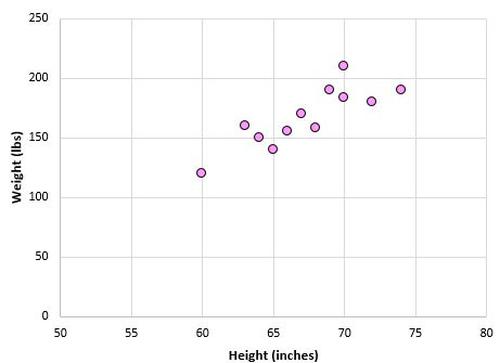Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt r = 0,836.

Die Teststatistik = .836 * √(12-2) / (1-.836²) = 4.804.

Laut unserem t-Verteilungsrechner hat ein t-Wert von 4,804 mit 10 Freiheitsgraden einen p-Wert von 0,0007. Da .0007 <.05 ist, können wir schließen, dass die Korrelation zwischen Gewicht und Größe in diesem Beispiel bei Alpha = .05 statistisch signifikant ist.

Vorsichtsmaßnahmen

Während ein Pearson-Korrelationskoeffizient hilfreich sein kann, um festzustellen, ob zwei Variablen eine lineare Assoziation haben oder nicht, müssen wir bei der Interpretation eines Pearson-Korrelationskoeffizienten drei Dinge berücksichtigen:

1. Korrelation bedeutet keine Kausalität. Nur weil zwei Variablen korreliert sind, bedeutet dies nicht, dass eine zwangsläufig dazu führt, dass die andere mehr oder weniger häufig auftritt. Ein klassisches Beispiel hierfür ist die positive Korrelation zwischen Eisverkäufen und Haiattacken. Wenn der Verkauf von Eiscreme zu bestimmten Jahreszeiten steigt, nehmen auch die Haiattacken tendenziell zu.

Bedeutet dies, dass der Verzehr von Eis Haiattacken verursacht? Natürlich nicht! Es bedeutet nur, dass im Sommer sowohl der Eiscremekonsum als auch die Haiattacken tendenziell zunehmen, da Eiscreme im Sommer beliebter ist und im Sommer mehr Menschen ins Meer gehen.

2. Korrelationen reagieren empfindlich auf Ausreißer. Ein extremer Ausreißer kann einen Pearson-Korrelationskoeffizienten dramatisch verändern. Betrachten Sie das folgende Beispiel:

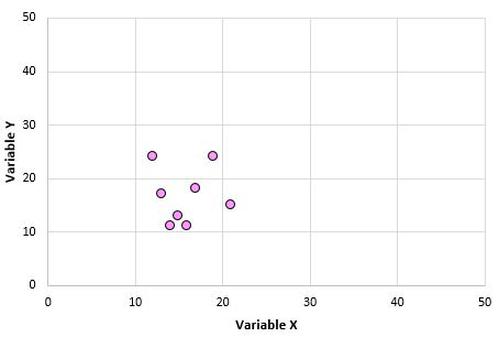Die Variablen X und Y haben einen Pearson-Korrelationskoeffizienten von 0,00. Stellen Sie sich jedoch vor, wir haben einen Ausreißer im Datensatz:

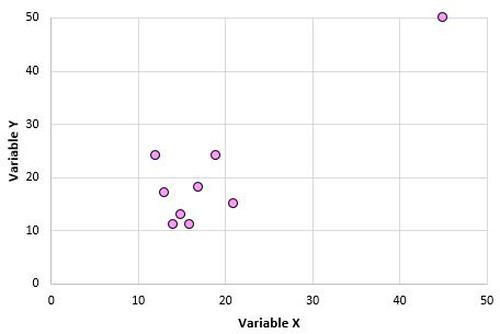Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt nun 0,878. Dieser eine Ausreißer verändert alles. Aus diesem Grund empfiehlt es sich, bei der Berechnung der Korrelation für zwei Variablen die Variablen mithilfe eines Streudiagramms zu visualisieren, um nach Ausreißern zu suchen.

3. Ein Pearson-Korrelationskoeffizient erfasst keine nichtlinearen Beziehungen zwischen zwei Variablen. Stellen Sie sich vor, wir haben zwei Variablen mit der folgenden Beziehung:

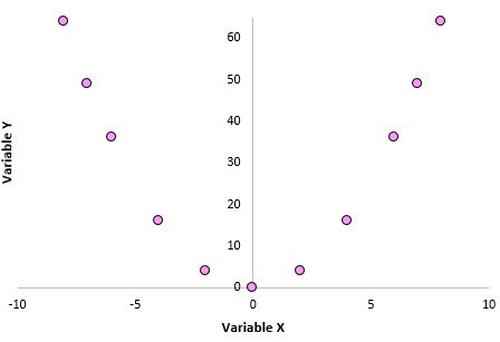Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt 0,00, da sie keine lineare Beziehung haben. Diese beiden Variablen haben jedoch eine nichtlineare Beziehung: Die y-Werte sind einfach die quadratischen x-Werte.

Beachten Sie bei der Verwendung des Pearson-Korrelationskoeffizienten, dass Sie lediglich testen, ob zwei Variablen linear zusammenhängen. Selbst wenn ein Pearson-Korrelationskoeffizient angibt, dass zwei Variablen nicht korreliert sind, können sie dennoch eine nichtlineare Beziehung haben. Dies ist ein weiterer Grund, warum es hilfreich ist, bei der Analyse der Beziehung zwischen zwei Variablen ein Streudiagramm zu erstellen. Dies kann Ihnen dabei helfen, eine nichtlineare Beziehung zu erkennen.