So finden Sie P-Werte in Google Tabellen (Schritt für Schritt)

Der einfachste Weg, p-Werte in Google Tabellen zu berechnen, ist die Verwendung der Funktion T.TEST(), die den mit einem t-Test verknüpften p-Wert findet und die folgende Syntax verwendet:

T.TEST(range 1, range2, tails, type)

wo:

• range1: Das erste Datensample
• range2: Die zweite Datenprobe
• tails: Die Anzahl der Seiten, die für den Test verwendet werden sollen
• 1: Einseitiger (oder „einseitiger“) t-Test
• 2: Zweiseitiger (oder „zweiseitiger) t-Test
• Typ: Der Typ des t-Tests
• 1: Gepaarter t-Test
• 2: Zwei-Stichproben-t-Test mit gleicher Varianz
• 3: Zwei-Stichproben-t-Test mit ungleicher Varianz

Diese Funktion gibt den p-Wert zurück, der dem t-Test entspricht.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie diese Funktion in der Praxis verwenden können.

Schritt 1: Erstellen Sie die Daten

Lassen Sie uns zunächst einen gefälschten Datensatz erstellen, der die Höhe von zwei verschiedenen Pflanzenarten enthält:

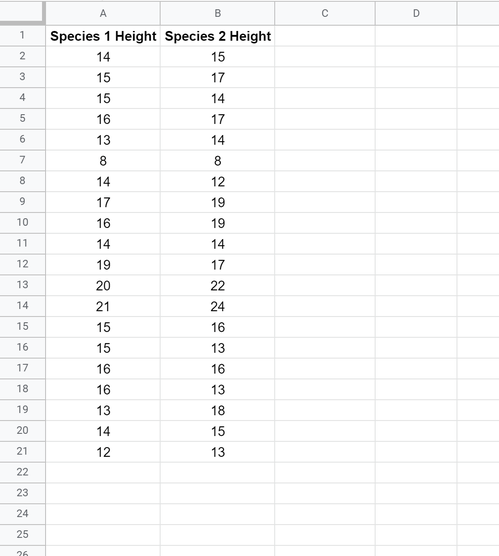
Schritt 2: Berechnen Sie den P-Wert des t-Tests

Nehmen wir als Nächstes an, wir wollen einen t-Test durchführen, um festzustellen, ob die mittlere Höhe zwischen den beiden Pflanzenarten gleich ist.

Die folgenden Screenshots zeigen, welche Formeln zur Berechnung der p-Werte der Tests zu verwenden sind.

t-Test für gepaarte Stichproben

Wir können die folgende Formel verwenden, um den p-Wert für einen t-Test bei gepaarten Stichproben zu berechnen:

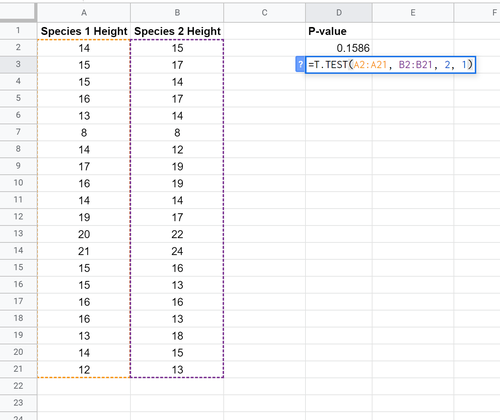
Der p-Wert ergibt sich zu 0,1586. Da dieser nicht kleiner als α = 0,05 ist, verwerfen wir die Nullhypothese des Tests nicht. Wir haben keine ausreichenden Beweise, um zu sagen, dass die mittlere Höhe zwischen den beiden Arten unterschiedlich ist.

Zwei-Stichproben-t-Test mit gleicher Varianz

Wir können die folgende Formel verwenden, um den p-Wert für einen t-Test mit zwei Stichproben mit gleicher Varianz zu berechnen:

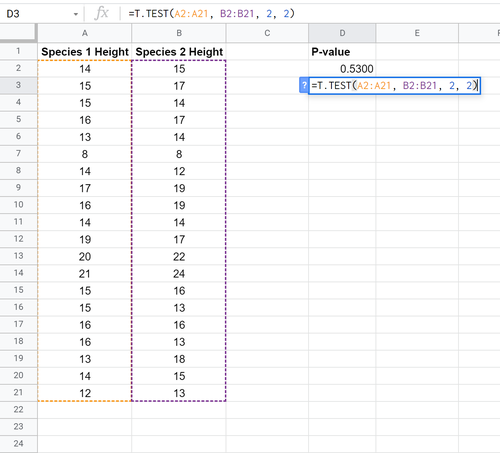
Der p-Wert stellt sich als 0,5300 heraus. Da dieser nicht kleiner als α = 0,05 ist, verwerfen wir die Nullhypothese des Tests nicht. Wir haben keine ausreichenden Beweise, um zu sagen, dass die mittlere Höhe zwischen den beiden Arten unterschiedlich ist.

t-Test bei zwei Stichproben mit ungleicher Varianz

Wir können die folgende Formel verwenden, um den p-Wert für einen t-Test mit zwei Stichproben und ungleicher Varianz zu berechnen:

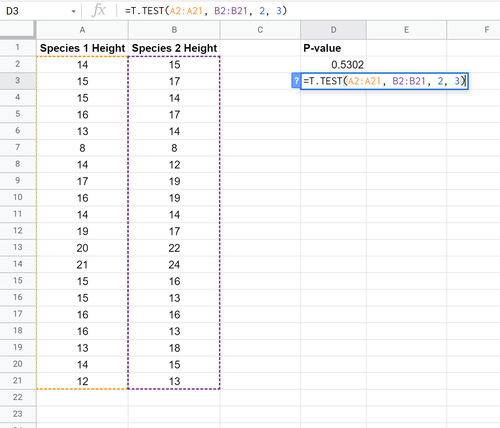
Der p-Wert ergibt sich zu 0,5302. Da dieser nicht kleiner als α = 0,05 ist, verwerfen wir die Nullhypothese des Tests nicht. Wir haben keine ausreichenden Beweise, um zu sagen, dass die mittlere Höhe zwischen den beiden Arten unterschiedlich ist.

Zusätzliche Ressourcen

Eine Erläuterung von p-Werten und statistischer Signifikanz
So führen Sie t-Tests in Google Tabellen durch
So führen Sie eine einfache ANOVA in Google Tabellen durch