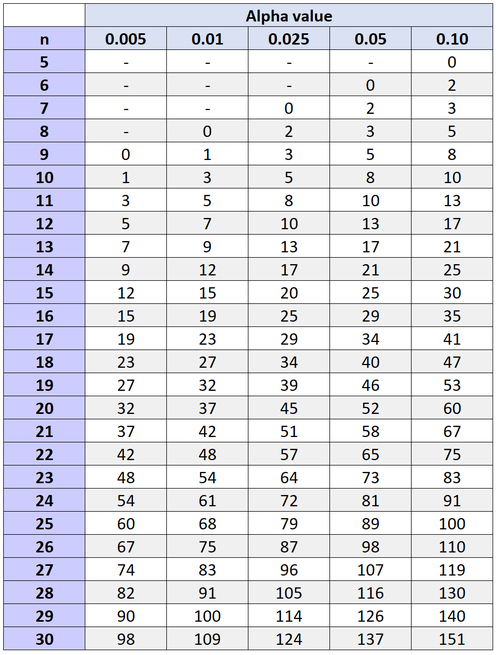
In der folgenden Tabelle sind die kritischen Werte für den Wilcoxon-Vorzeichen-Rang-Test aufgeführt.
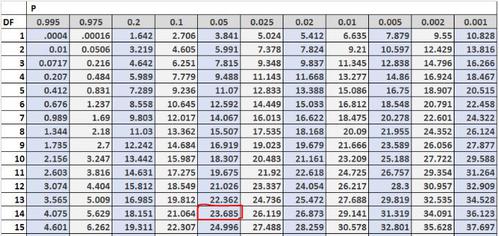
Die Chi-Quadrat-Verteilungstabelle ist eine Tabelle, die die kritischen Werte der Chi-Quadrat-Verteilung zeigt. Um die Chi-Quadrat-Verteilungstabelle zu verwenden, benötigen Sie nur zwei Werte:
- Ein Signifikanzniveau (übliche Auswahlmöglichkeiten sind 0,01, 0,05 und 0,10)
- Freiheitsgrade
Die Chi-Quadrat-Verteilungstabelle wird üblicherweise in den folgenden statistischen Tests verwendet:
Wenn Sie jeden dieser Tests durchführen, erhalten Sie eine Teststatistik X 2. Um herauszufinden, ob diese Teststatistik auf einem Alpha-Level statistisch signifikant ist, haben Sie zwei Möglichkeiten:
- Vergleichen Sie die Teststatistik X 2 mit einem kritischen Wert aus der Chi-Quadrat-Verteilungstabelle.
- Vergleichen Sie den p-Wert der Teststatistik X 2 auf ein gewähltes Alpha-Level.
Lassen Sie uns ein Beispiel für die Verwendung der einzelnen Ansätze durchgehen.
Beispiele
Angenommen, wir führen eine Art Chi-Quadrat-Test durch und erhalten eine Teststatistik X 2 von 27,42, und unsere Freiheitsgrade betragen 14. Wir möchten wissen, ob diese Ergebnisse statistisch signifikant sind.
Vergleichen Sie die Teststatistik X 2 auf einen kritischen Wert aus der Chi-Quadrat-Verteilungstabelle
Der erste Ansatz, mit dem wir feststellen können, ob unsere Ergebnisse statistisch signifikant sind, besteht darin, die Teststatistik X 2 zu vergleichen von 27,42 auf den kritischen Wert in der Chi-Quadrat-Verteilungstabelle. Der kritische Wert ist der Wert in der Tabelle, der mit einem Signifikanzwert von 0,05 und einem Freiheitsgrad von 14 übereinstimmt. Diese Zahl stellt sich als 23.685 heraus:
Da aus Teststatistik X 2 ( 27.42 ) größer als der kritische Wert ( 23.685 ) ist, lehnen wir die Nullhypothese unseres Tests ab. Wir haben genügend Beweise, um zu sagen, dass unsere Ergebnisse bei Alpha-Level 0,05 statistisch signifikant sind.
Vergleichen Sie den p-Wert der Teststatistik X2 auf ein gewähltes Alpha-Level
Der zweite Ansatz, mit dem wir feststellen können, ob unsere Ergebnisse statistisch signifikant sind, besteht darin, den p-Wert für die Teststatistik X 2 zu ermitteln von 27,42. Um diesen p-Wert zu finden, können wir die Chi-Quadrat-Verteilungstabelle nicht verwenden, da sie uns nur kritische Werte liefert, keine p-Werte.
Wann wird die Chi-Quadrat-Verteilungstabelle verwendet?
Wenn Sie daran interessiert sind, den kritischen Chi-Quadrat-Wert für ein bestimmtes Signifikanzniveau und bestimmte Freiheitsgrade zu ermitteln, sollten Sie die Chi-Quadrat-Verteilungstabelle verwenden.
Wilcoxon-Vorzeichen-Rang-Tabelle
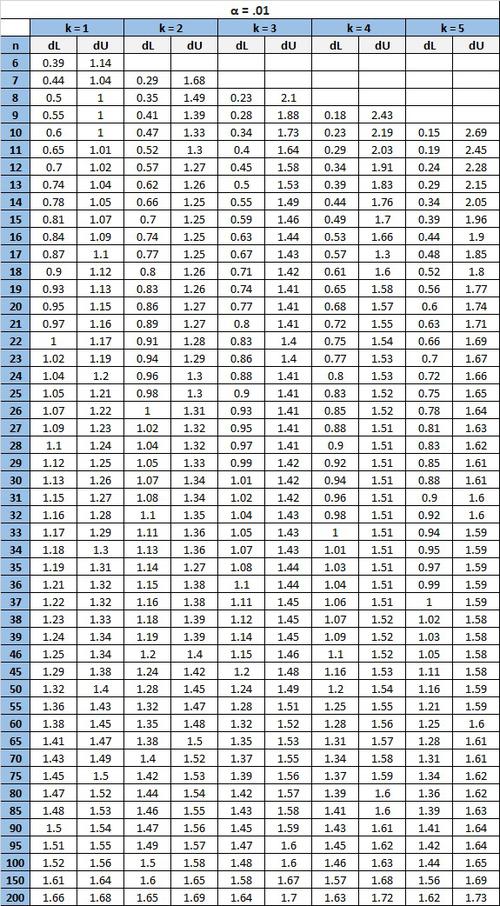
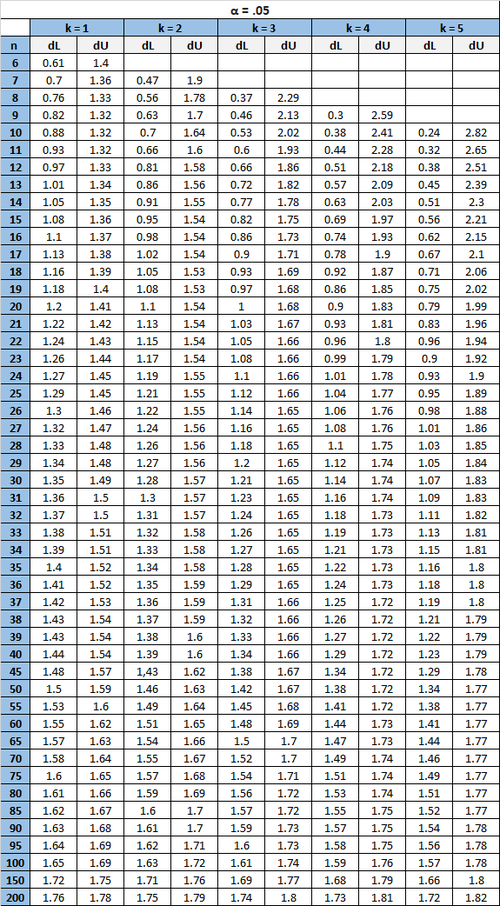
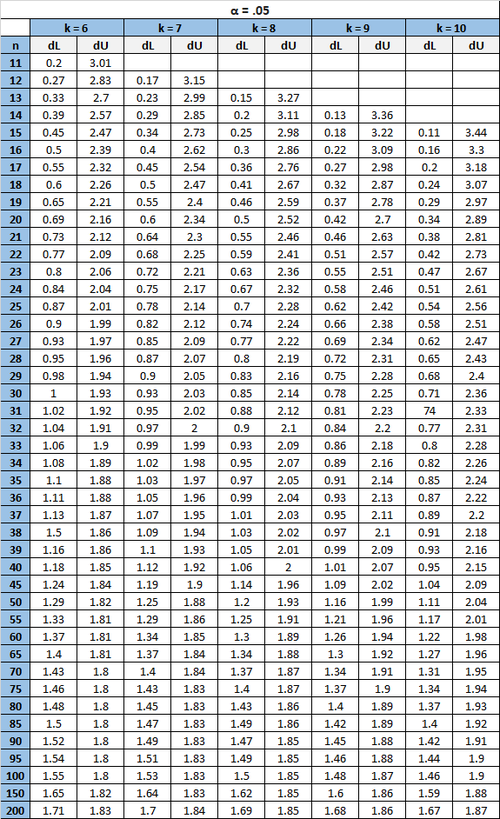
Durbin-Watson-Tabelle
Die folgende Tabelle enthält die kritischen Werte für den Durbin-Watson-Test für eine bestimmte Stichprobengröße (n), Anzahl der unabhängigen Variablen (k) und Alpha-Level.