So testen Sie auf Normalverteilung in Stata

Bei vielen statistischen Tests müssen eine oder mehrere Variablen normalverteilt sein, damit die Testergebnisse zuverlässig sind.

In diesem Artikel werden verschiedene Methoden erläutert, mit denen Sie die Normalverteilung von Variablen in Stata testen können.

Für jede dieser Methoden verwenden wir das integrierte Stata-Dataset namens car. Sie können diesen Datensatz mit dem folgenden Befehl laden:

sysuse car

Methode 1: Histogramme

Eine informelle Möglichkeit, um festzustellen, ob eine Variable normalverteilt ist, besteht darin, ein Histogramm zu erstellen, um die Verteilung der Variablen anzuzeigen. Wenn die Variable normalverteilt ist, sollte das Histogramm nehmen eine „Glocke“-Form mit mehreren Werten in der Nähe der Mitte und weniger Werte auf den Schwänzen entfernt werden.

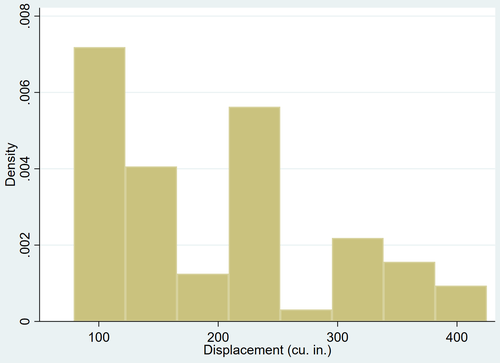
Mit dem Befehl hist können wir ein Histogramm für die variable displacement erstellen:

hist displacement

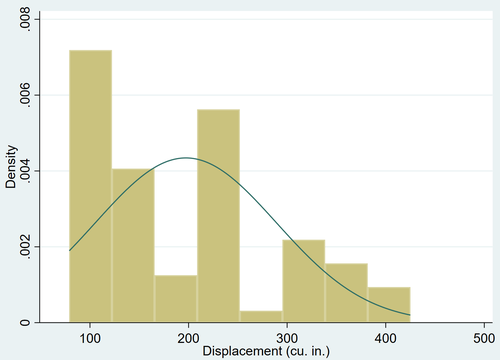
Mit dem Befehl normal können wir einem Histogramm eine Kurve mit normaler Dichte hinzufügen:

hist displacement, normal

Es ist ziemlich offensichtlich, dass die Variable displacement nach rechts verschoben ist (z. B. konzentrieren sich die meisten Werte auf die linke Seite und ein langer "Schwanz" von Werten erstreckt sich nach rechts) und keiner Normalverteilung folgt.

Methode 2: Shapiro-Wilk-Test

Eine formale Möglichkeit, auf Normalverteilung zu testen, ist die Verwendung des Shapiro-Wilk-Tests. Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (übliche Auswahlmöglichkeiten sind 0,01, 0,05 und 0,10), können wir die Nullhypothese ablehnen und daraus schließen, dass es genügend Beweise gibt, um zu sagen, dass die Variable nicht normalverteilt ist.

* Dieser Test kann verwendet werden, wenn die Gesamtzahl der Beobachtungen zwischen 4 und 2.000 liegt.

Mit dem Befehl swilk können wir einen Shapiro-Wilk-Test für die Variable displacement durchführen :

swilk displacement

So interpretieren Sie die Ausgabe des Tests:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

W: 0,92542. Dies ist die Teststatistik für den Test.

Prob z: 0,00031. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen. Wir haben genügend Beweise, um zu sagen, dass die Variable displacement nicht normalverteilt ist.

Wir können den Shapiro-Wilk-Test auch für mehrere Variablen gleichzeitig durchführen, indem wir nach dem Befehl swilk mehrere Variablen auflisten:

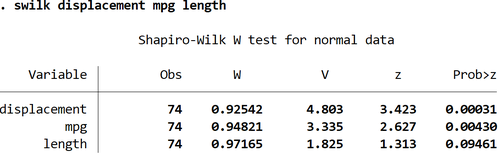
swilk displacement mpg length

Unter Verwendung eines Signifikanzniveaus von 0,05 würden wir schlussfolgern, dass sowohl displacement als auch mpg nicht normalverteilt sind, aber wir haben nicht genügend Beweise, um zu sagen, dass die length nicht normalverteilt ist.

Methode 3: Shapiro-Francia-Test

Eine andere formale Möglichkeit, auf Normalverteilung zu testen, ist die Verwendung des Shapiro-Francia-Tests. Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass es genügend Beweise gibt, um zu sagen, dass die Variable nicht normalverteilt ist.

* Dieser Test kann verwendet werden, wenn die Gesamtzahl der Beobachtungen zwischen 10 und 5.000 liegt.

Mit dem Befehl sfrancia können wir einen Shapiro-Wilk-Test für die Variable displacement durchführen :

sfrancia displacement

So interpretieren Sie die Ausgabe des Tests:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

W ‚: 0,93011. Dies ist die Teststatistik für den Test.

Prob> z: 0,00094. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen. Wir haben genügend Beweise, um zu sagen, dass die Variable displacement nicht normalverteilt ist.

Ähnlich wie beim Shapiro-Wilk-Test können Sie den Shapiro-Francia-Test für mehrere Variablen gleichzeitig durchführen, indem Sie nach dem Befehl sfrancia mehrere Variablen auflisten.

Methode 4: Skewness- und Kurtosis-Test

Eine andere Möglichkeit, auf Normalverteilung zu testen, ist die Verwendung des Skewness- und Kurtosis-Tests (dt. Schiefe und Wölbung), mit dem festgestellt wird, ob die Skewness und die Kurtosis einer Variablen mit der Normalverteilung übereinstimmen.

Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass es genügend Beweise gibt, um zu sagen, dass die Variable nicht normalverteilt ist.

* Für diesen Test müssen mindestens 8 Beobachtungen verwendet werden.

Mit dem Befehl sktest können wir einen Skewness- und Kurtosis-Test für die Variable displacementdurchführen :

sktest displacement

So interpretieren Sie die Ausgabe des Tests:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

adj chi (2): 5,81. Dies ist die Chi-Quadrat-Teststatistik für den Test.

Prob> chi2: 0,0547. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert nicht weniger als 0,05 beträgt, können wir die Nullhypothese des Tests nicht ablehnen. Wir haben nicht genügend Beweise, um zu sagen, dass displacement nicht normalverteilt ist.

Ähnlich wie bei den anderen Normalverteilungstests können Sie den Skewness- und Kurtosis-Test für mehrere Variablen gleichzeitig durchführen, indem Sie nach dem Befehl sktest mehrere Variablen auflisten.