Eine Einführung in die Multinomialverteilung

Die Multinomialverteilung beschreibt die Wahrscheinlichkeit, eine bestimmte Anzahl von Zählungen für k verschiedene Ergebnisse zu erhalten, wenn jedes Ergebnis eine feste Eintrittswahrscheinlichkeit hat.

Wenn eine Zufallsvariable X einer multinomialen Verteilung folgt, kann die Wahrscheinlichkeit, dass Ergebnis 1 genau x₁ mal, Ergebnis 2 genau x₂ mal, Ergebnis 3 genau x₃ mal usw. auftritt, durch die folgende Formel ermittelt werden:

Wahrscheinlichkeit = n! * (p₁^x₁ * p₂^x₂ *… * p_k^x_k) / (x₁! * x₂!… * x_k!)

wobei:

• n: Gesamtzahl der Ereignisse
• x ₁: Häufigkeit, mit der Ergebnis 1 auftritt
• p ₁: Wahrscheinlichkeit, dass Ergebnis 1 in einem bestimmten Versuch auftritt

Angenommen, eine Urne enthält 5 rote Murmeln, 3 grüne Murmeln und 2 blaue Murmeln. Wenn wir zufällig 5 Murmeln aus der Urne mit Ersatz auswählen, wie hoch ist die Wahrscheinlichkeit, genau 2 rote Murmeln, 2 grüne Murmeln und 1 blauen Marmor zu erhalten?

Um dies zu beantworten, können wir die Multinomialverteilung mit den folgenden Parametern verwenden:

• n: 5
• x₁ (# rote Murmeln) = 2, x₂ (# grüne Murmeln) = 2, x₃ (# blaue Murmeln) = 1
• p₁ (wahrscheinlich rot) = 0,5, p₂ (wahrscheinlich grün) = 0,3, p₃ (wahrscheinlich blau) = 0,2

Wenn wir diese Zahlen in die Formel einfügen, ergibt sich folgende Wahrscheinlichkeit:

Wahrscheinlichkeit = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135.

Probleme bei der multinomialen Verteilungspraxis

Verwenden Sie die folgenden Übungsprobleme, um Ihr Wissen über die Multinomialverteilung zu testen.

Problem 1

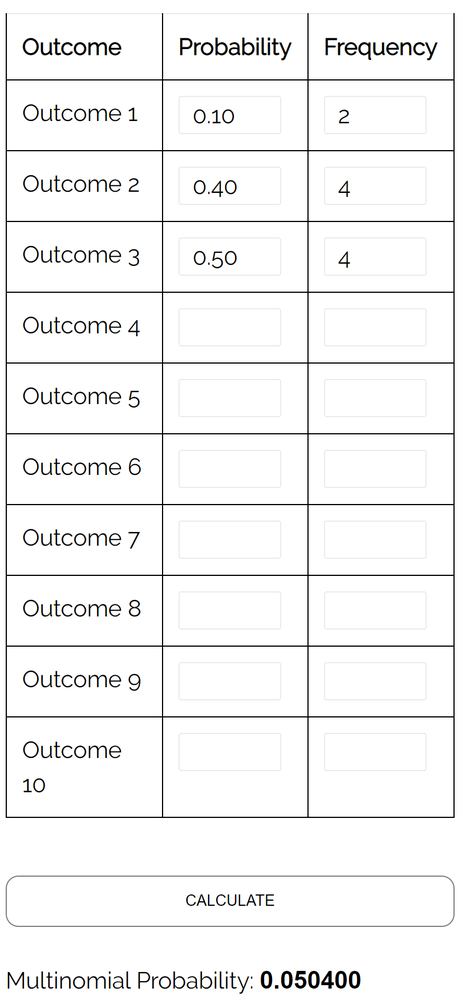
Frage: Bei einer Drei-Wege-Wahl zum Bürgermeister erhält Kandidat A 10% der Stimmen, Kandidat B 40% der Stimmen und Kandidat C 50% der Stimmen. Wenn wir eine Zufallsstichprobe von 10 Wählern auswählen, wie hoch ist die Wahrscheinlichkeit, dass 2 für Kandidat A, 4 für Kandidat B und 4 für Kandidat C gestimmt haben?

Antwort: Unter Verwendung des Multinomialverteilungsrechners mit den folgenden Eingaben stellen wir fest, dass die Wahrscheinlichkeit 0,0504 beträgt :

Problem 2

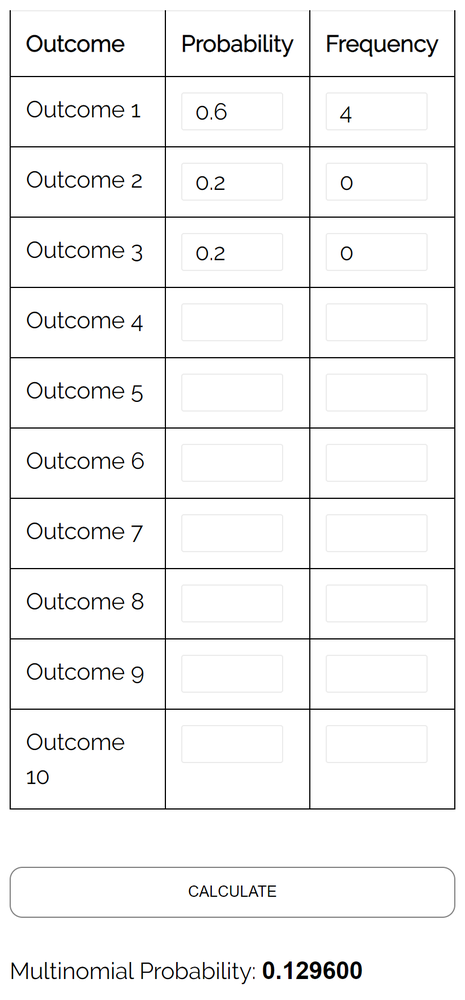
Frage: Angenommen, eine Urne enthält 6 gelbe Murmeln, 2 rote Murmeln und 2 rosa Murmeln. Wenn wir zufällig 4 Bälle aus der Urne auswählen und ersetzen, wie hoch ist die Wahrscheinlichkeit, dass alle 4 Bälle gelb sind?

Antwort: Unter Verwendung des Multinomialverteilungsrechners mit den folgenden Eingaben stellen wir fest, dass die Wahrscheinlichkeit 0,1296 beträgt :

Problem 3

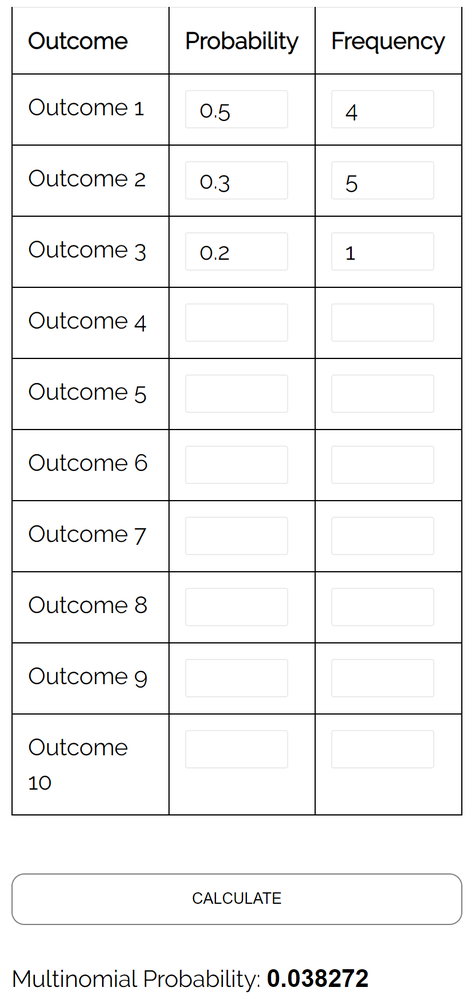
Frage: Angenommen, zwei Schüler spielen Schach gegeneinander. Die Wahrscheinlichkeit, dass Schüler A ein bestimmtes Spiel gewinnt, beträgt 0,5, die Wahrscheinlichkeit, dass Schüler B ein bestimmtes Spiel gewinnt, beträgt 0,3 und die Wahrscheinlichkeit, dass sie in einem bestimmten Spiel unentschieden spielen, beträgt 0,2. Wenn sie 10 Spiele spielen, wie hoch ist die Wahrscheinlichkeit, dass Spieler A 4 Mal gewinnt, Spieler B 5 Mal gewinnt und 1 Mal unentschieden spielt?

Antwort: Unter Verwendung des Multinomialverteilungsrechners mit den folgenden Eingaben stellen wir fest, dass die Wahrscheinlichkeit 0,038272 beträgt :