Eine schnelle Einführung in die Leave-One-Out-Kreuzvalidierung (LOOCV)

Um die Leistung eines Modells in einem Datensatz zu bewerten, müssen wir messen, wie gut die vom Modell gemachten Vorhersagen mit den beobachteten Daten übereinstimmen.

Die gebräuchlichste Methode, um dies zu messen, ist die Verwendung des mittleren quadratischen Fehlers (MSE), der wie folgt berechnet wird:

MSE = (1 / n) * Σ (y _i - f (x _i )) ²

wo:

• n: Gesamtzahl der Beobachtungen
• y _i: Der Antwortwert der i-ten Beobachtung
• f (x _i ): Der vorhergesagte Antwortwert der i-ten Beobachtung

Je näher die Modellvorhersagen an den Beobachtungen liegen, desto kleiner wird der MSE.

In der Praxis verwenden wir den folgenden Prozess, um der MSE eines bestimmten Modells zu berechnen:

1. Teilen Sie einen Datensatz in einen Trainingssatz und einen Testdatensatz auf.

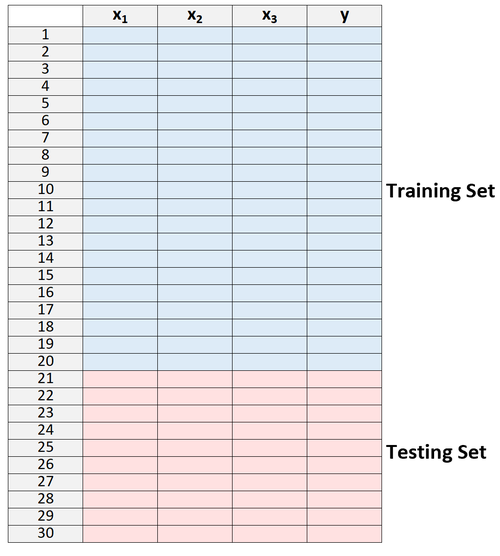
2. Erstellen Sie das Modell nur mit Daten aus dem Trainingssatz.

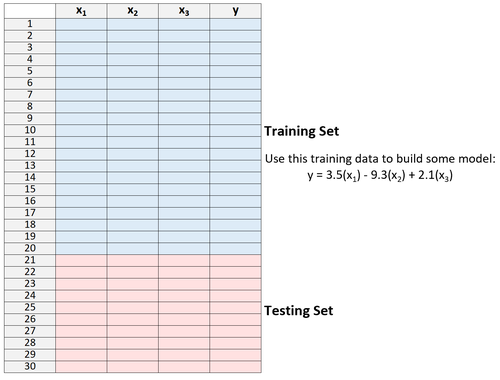
3. Verwenden Sie das Modell, um Vorhersagen für den Testdatensatz zu treffen und der MSE zu messen - dies wird als Test-MSE bezeichnet.

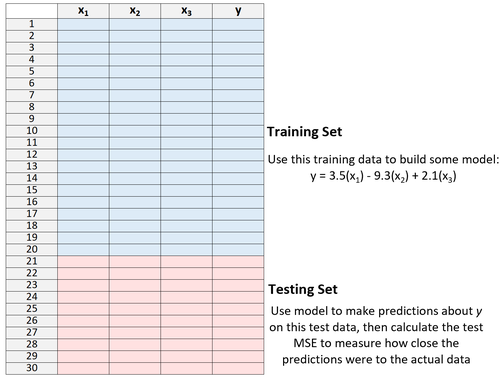
Der Test-MSE gibt uns eine Vorstellung davon, wie gut ein Modell mit Daten funktioniert, die es zuvor noch nicht gesehen hat,d.h.mit Daten, die nicht zum „Trainieren“ des Modells verwendet wurden.

Der Nachteil der Verwendung nur eines Testdatensatzes besteht jedoch darin, dass der Test-MSE stark variieren kann, je nachdem, welche Beobachtungen in den Trainings- und Testsätzen verwendet wurden.

Es ist möglich, dass sich unserer Test-MSE als viel größer oder kleiner herausstellt, wenn wir einen anderen Datensatz von Beobachtungen für den Trainingssatz und den Testdatensatz verwenden.

Eine Möglichkeit, dieses Problem zu vermeiden, besteht darin, ein Modell mehrmals mit einem anderen Trainings- und Testdatensatz anzupassen und dann der Test-MSE als Durchschnitt aller Test-MSEs zu berechnen.

Diese allgemeine Methode wird als Kreuzvalidierung bezeichnet, und eine bestimmte Form davon wird als Leave-One-Out-Kreuzvalidierung bezeichnet.

Leave-One-Out-Kreuzvalidierung

Die Leave-One-Out-Kreuzvalidierung verwendet den folgenden Ansatz, um ein Modell zu bewerten:

1. Teilen Sie einen Datensatz in einen Trainingssatz und einen Testdatensatz auf, wobei Sie alle Beobachtungen bis auf eine als Teil des Trainingssatzes verwenden:

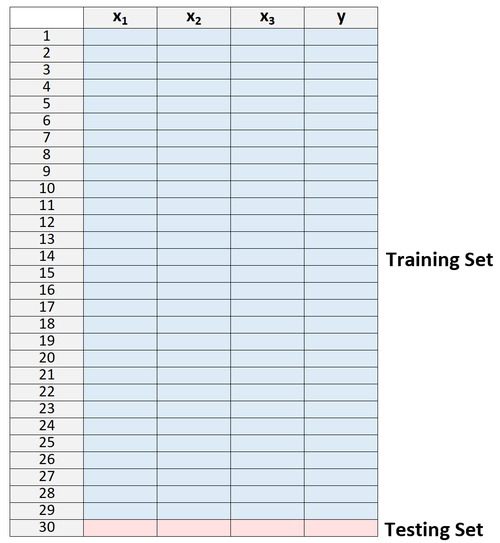
Beachten Sie, dass wir nur eine Beobachtung aus dem Trainingssatz herauslassen. Hier erhält die Methode den Namen "Leave-One-Out-Kreuzvalidierung".

2. Erstellen Sie das Modell nur mit Daten aus dem Trainingssatz.

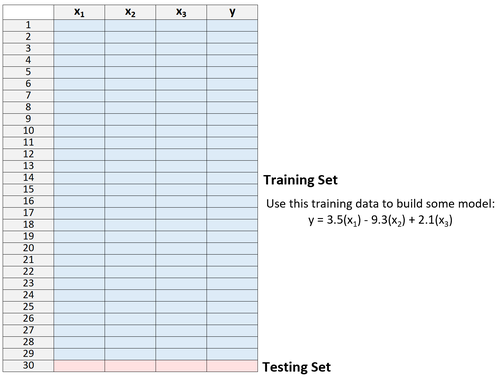
3. Verwenden Sie das Modell, um den Antwortwert der einen aus dem Modell ausgelassenen Beobachtung vorherzusagen und der MSE zu berechnen.

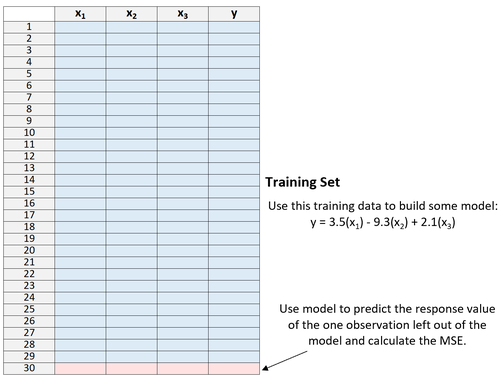
4. Wiederholen Sie den Vorgang n-mal.

Zuletzt wiederholen wir diesen Vorgang n-mal (wobei n die Gesamtzahl der Beobachtungen im Datensatz ist) und lassen jedes Mal eine andere Beobachtung aus dem Trainingssatz aus.

Wir berechnen dann der Test-MSE als Durchschnitt aller Test-MSEs:

Test MSE = (1 / n) * ΣMSE _i

wo:

• n: Die Gesamtzahl der Beobachtungen im Datensatz
• MSEi: Der Test-MSE während der i-ten Zeit der Anpassung des Modells.

Vor- und Nachteile von LOOCV

Eine Leave-One-Out-Kreuzvalidierung bietet die folgenden Vorteile:

• Es bietet ein viel weniger voreingenommenes Maß für der Test-MSE als die Verwendung eines einzelnen Testdatensatzes, da wir ein Modell wiederholt an einen Datensatz anpassen, der n-1-Beobachtungen enthält.
• Der Test-MSE wird im Vergleich zur Verwendung eines einzelnen Testdatensatzes nicht überschätzt.

Eine Leave-One-Out-Kreuzvalidierung hat jedoch folgende Nachteile:

• Es kann ein zeitaufwändiger Prozess sein, wenn n groß ist.
• Es kann auch zeitaufwändig sein, wenn ein Modell besonders komplex ist und lange dauert, bis es in einen Datensatz passt.
• Es kann rechenintensiv sein. Glücklicherweise ist modernes Computing in den meisten Bereichen so effizient geworden, dass LOOCV im Vergleich zu vor vielen Jahren eine viel vernünftigere Methode ist.

Beachten Sie, dass LOOCV sowohl in Regressions- als auch in Klassifizierungseinstellungen verwendet werden kann. Für Regressionsprobleme wird der Test-MSE als mittlere quadratische Differenz zwischen Vorhersagen und Beobachtungen berechnet, während bei Klassifizierungsproblemen der Test-MSE als Prozentsatz der Beobachtungen berechnet wird, die während der n wiederholten Modellanpassungen korrekt klassifiziert wurden.

So führen Sie LOOCV in R & Python durch

Die folgenden Tutorials enthalten schrittweise Beispiele für die Durchführung von LOOCV für ein bestimmtes Modell in R und Python:

Leave-One-Out-Kreuzvalidierung in R
Leave-One-Out-Kreuzvalidierung in Python