Lesen einer Korrelationsmatrix

In der Statistik sind wir oft daran interessiert, die Beziehung zwischen zwei Variablen zu verstehen.

Zum Beispiel möchten wir vielleicht die Beziehung zwischen der Anzahl der Stunden, die ein Student studiert, und der Prüfungsnote, die er erhält, verstehen.

Eine Möglichkeit, diese Beziehung zu quantifizieren, besteht darin, den Pearson-Korrelationskoeffizienten zu verwenden, der ein Maß für die lineare Assoziation zwischen zwei Variablen ist . Es hat einen Wert zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 zeigt keine lineare Korrelation zwischen zwei Variablen an
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Je weiter der Korrelationskoeffizient von Null entfernt ist, desto stärker ist die Beziehung zwischen den beiden Variablen.

Verwandt: Was wird als „starke“ Korrelation angesehen?

In einigen Fällen möchten wir jedoch die Korrelation zwischen mehr als nur einem Variablenpaar verstehen. In diesen Fällen können wir eine Korrelationsmatrix erstellen, bei der es sich um eine quadratische Tabelle handelt, die die Korrelationskoeffizienten zwischen mehreren Variablen zeigt.

Beispiel einer Korrelationsmatrix

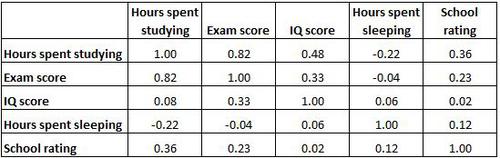
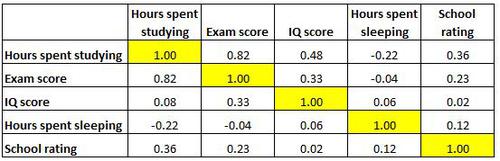
Die folgende Korrelationsmatrix zeigt die Korrelationskoeffizienten zwischen verschiedenen Variablen im Zusammenhang mit Bildung:

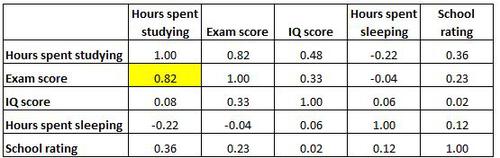
Jede Zelle in der Tabelle zeigt die Korrelation zwischen zwei spezifischen Variablen. Die hervorgehobene Zelle unten zeigt beispielsweise, dass die Korrelation zwischen „Stunden des Studiums“ und „Prüfungsergebnis“ 0,82 beträgt, was darauf hinweist, dass sie stark positiv korreliert sind. Mehr Stunden für das Studium hängen stark mit höheren Prüfungsergebnissen zusammen.

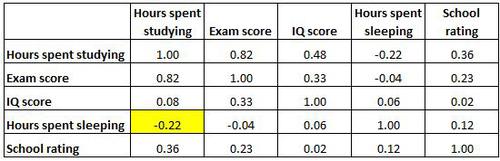
Die hervorgehobene Zelle unten zeigt, dass die Korrelation zwischen Lernstunden (study hours) und Schlafstunden (sleep hours) -0,22 beträgt, was darauf hinweist, dass sie schwach negativ korreliert sind. Mehr Stunden mit Lernen sind mit weniger Stunden Schlaf verbunden.

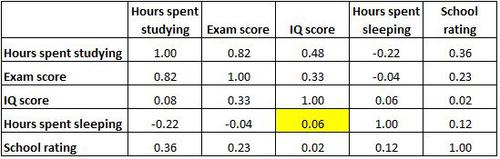
Die hervorgehobene Zelle unten zeigt, dass die Korrelation zwischen „Schlafstunden“ und „IQ-Wert“ 0,06 beträgt, was darauf hinweist, dass sie im Grunde genommen nicht korreliert sind. Es gibt nur einen sehr geringen Zusammenhang zwischen der Anzahl der Schlafstunden eines Schülers und seinem IQ-Wert.

Beachten Sie auch, dass die Korrelationskoeffizienten entlang der Diagonale der Tabelle alle gleich 1 sind, da jede Variable perfekt mit sich selbst korreliert. Diese Zellen sind für die Interpretation nicht nützlich.

Variationen der Korrelationsmatrix

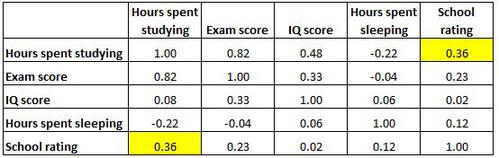
Beachten Sie, dass eine Korrelationsmatrix perfekt symmetrisch ist. Beispielsweise zeigt die obere rechte Zelle genau den gleichen Wert wie die untere linke Zelle:

Dies liegt daran, dass beide Zellen die Korrelation zwischen „Lernstunden“ und „Schulbewertung“ messen.

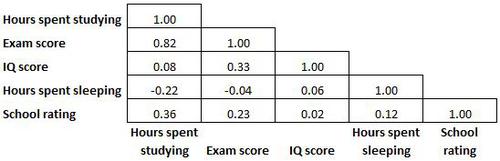
Da eine Korrelationsmatrix symmetrisch ist, ist die Hälfte der in der Matrix gezeigten Korrelationskoeffizienten redundant und unnötig. Daher wird manchmal nur die Hälfte der Korrelationsmatrix angezeigt:

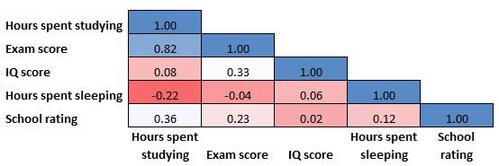
Und manchmal wird eine Korrelationsmatrix wie eine Wärmekarte eingefärbt, um das Lesen der Korrelationskoeffizienten noch einfacher zu machen:

Wann wird eine Korrelationsmatrix verwendet?

In der Praxis wird eine Korrelationsmatrix üblicherweise aus drei Gründen verwendet:

1. Eine Korrelationsmatrix fasst einen Datensatz bequem zusammen.

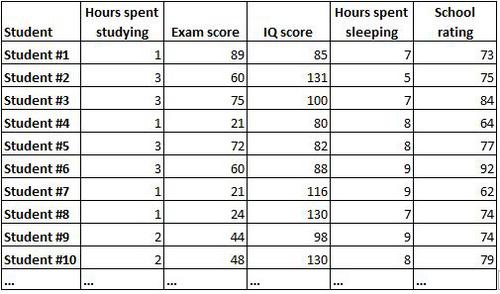
Eine Korrelationsmatrix ist eine einfache Möglichkeit, die Korrelationen zwischen allen Variablen in einem Datensatz zusammenzufassen. Angenommen, wir haben den folgenden Datensatz mit den folgenden Informationen für 1.000 Schüler:

Es wäre sehr schwierig, die Beziehung zwischen den einzelnen Variablen zu verstehen, wenn man einfach auf die Rohdaten starrt. Glücklicherweise kann uns eine Korrelationsmatrix helfen, die Korrelationen zwischen jedem Variablenpaar schnell zu verstehen.

2. Eine Korrelationsmatrix dient als Diagnose für die Regression.

Eine wichtige Annahme der multiplen linearen Regression ist, dass keine unabhängige Variable im Modell stark mit einer anderen Variablen im Modell korreliert. Wenn zwei unabhängige Variablen stark korreliert sind, führt dies zu einem Problem, das als Multikollinearität bekannt ist, und es kann schwierig sein, die Ergebnisse der Regression zu interpretieren.

Eine der einfachsten Möglichkeiten, ein potenzielles Multikollinearitätsproblem zu erkennen, besteht darin, eine Korrelationsmatrix zu betrachten und visuell zu überprüfen, ob eine der Variablen stark miteinander korreliert.

3. Eine Korrelationsmatrix kann als Eingabe für andere Analysen verwendet werden.

Eine Korrelationsmatrix wird als Eingabe für andere komplexe Analysen wie die explorative Faktoranalyse und Strukturgleichungsmodelle verwendet.

Zusätzliche Ressourcen

So erstellen Sie eine Korrelationsmatrix in Excel
So erstellen Sie eine Korrelationsmatrix in SPSS
So erstellen Sie eine Korrelationsmatrix in Stata
So erstellen Sie eine Korrelationsmatrix in Python