So berechnen Sie Konfidenzintervalle in Excel

Ein Konfidenzintervall ist ein Wertebereich, der wahrscheinlich einen Populationsparameter mit einem bestimmten Konfidenzniveau enthält. Es wird nach der folgenden allgemeinen Formel berechnet:

Konfidenzintervall = (Punktschätzung) +/- (kritischer Wert)*(Standardfehler)

Diese Formel erstellt ein Intervall mit einer unteren und einer oberen Grenze, das wahrscheinlich einen Populationsparameter mit einem bestimmten Vertrauensniveau enthält:

Konfidenzintervall = [untere Grenze, obere Grenze]

In diesem Tutorial wird erläutert, wie Sie die folgenden Konfidenzintervalle in Excel berechnen:

1. Konfidenzintervall für einen Mittelwert

2. Konfidenzintervall für einen Mittelwertunterschied

3. Konfidenzintervall für einen Anteil

4. Konfidenzintervall für Proportionsunterschiede

Lass uns einspringen!

Beispiel 1: Konfidenzintervall für einen Mittelwert

Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Mittelwert zu berechnen:

Konfidenzintervall = x +/- z*(s/√n)

wo:

• x: Stichprobenmittelwert
• z: der gewählte z-Wert
• s: Standardabweichung der Stichprobe
• n: Stichprobengröße

Beispiel: Angenommen, wir sammeln eine zufällige Stichprobe von Schildkröten mit den folgenden Informationen:

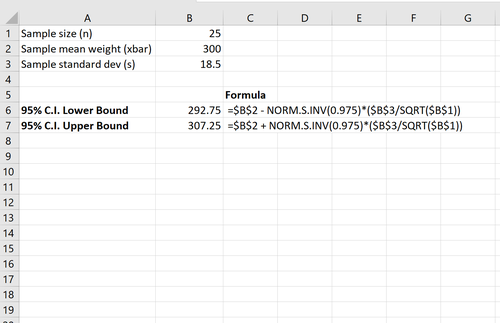
• Stichprobengröße n = 25
• Stichprobenmittelgewicht x = 300
• Standardabweichung der Stichprobe s = 18,5

Der folgende Screenshot zeigt, wie ein 95%-Konfidenzintervall für das tatsächliche mittlere Populationsgewicht der Schildkröten berechnet wird:

Das 95-%-Konfidenzintervall für das wahre mittlere Populationsgewicht der Schildkröten beträgt [292,75, 307.25].

Beispiel 2: Konfidenzintervall für einen Mittelwertunterschied

Wir verwenden die folgende Formel, um ein Konfidenzintervall für eine Differenz der Populationsmittelwerte zu berechnen:

Konfidenzintervall = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

wo:

• x ₁, x ₂: Mittelwert von Probe 1, Mittelwert von Probe 2
• t: der t-kritische Wert basierend auf dem Konfidenzniveau und (n ₁ +n ₂ -2) Freiheitsgraden
• s _p ^2: gepoolte Varianz, berechnet als ((n ₁ -1) s ₁ ² + (n ₂ -1) s ₂ ²⁾ / (n ₁ + n ₂ -2)
• t: der t-kritische Wert
• n ₁, n ₂: Stichprobe 1 Größe, Stichprobe 2 Größe

Beispiel: Angenommen, wir möchten den Unterschied im mittleren Gewicht zwischen zwei verschiedenen Schildkrötenarten schätzen, also ziehen wir eine Zufallsstichprobe von 15 Schildkröten aus jeder Population zusammen. Hier sind die zusammenfassenden Daten für jede Probe:

Beispiel 1:

• x ₁ = 310
• s ₁ = 18,5
• n ₁ = 15

Probe 2:

• x ₂ = 300
• s ₂ = 16,4
• n ₂ = 15

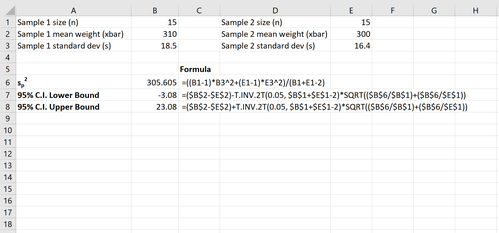
Der folgende Screenshot zeigt, wie ein 95 %-Konfidenzintervall für die wahre Differenz der Populationsmittelwerte berechnet wird:

Das 95 %-Konfidenzintervall für die wahre Differenz der Populationsmittelwerte beträgt [-3,08, 23,08].

Beispiel 3: Konfidenzintervall für einen Anteil

Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Anteil zu berechnen:

Konfidenzintervall =   +/-  z*√p(1-p) / n

wo:

• p: Probenanteil
• z: der gewählte z-Wert
• n: Stichprobengröße

Beispiel: Angenommen, wir möchten den Anteil der Einwohner eines Landkreises schätzen, die ein bestimmtes Gesetz befürworten. Wir wählen eine Zufallsstichprobe von 100 Einwohnern aus und befragen sie zu ihrer Haltung zum Gesetz. Hier sind die Ergebnisse:

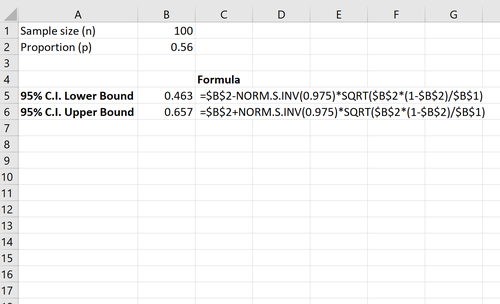
• Stichprobengröße n = 100
• Anteil zugunsten des Gesetzes p = 0,56

Der folgende Screenshot zeigt, wie ein 95%-Konfidenzintervall für den wahren Anteil der Einwohner im gesamten Landkreis berechnet wird, die das Gesetz befürworten:

Das 95-%-Konfidenzintervall für den wahren Anteil der Einwohner im gesamten Landkreis, die das Gesetz befürworten, beträgt [.463, .657].

Beispiel 4: Konfidenzintervall für eine Proportionsdifferenz

Wir verwenden die folgende Formel, um ein Konfidenzintervall für eine Proportionsdifferenz zu berechnen:

Konfidenzintervall = (p ₁ –p ₂ ) +/- z*√(p ₁ (1-p ₁ )/n ₁ + p ₂ (1-p ₂ )/n ₂ )

wo:

• p ₁, p ₂: Anteil Probe 1, Anteil Probe 2
• z: der z-kritische Wert basierend auf dem Konfidenzniveau
• n ₁, n ₂: Stichprobe 1 Größe, Stichprobe 2 Größe

Beispiel: Angenommen, wir möchten den Unterschied im Anteil der Einwohner, die ein bestimmtes Gesetz in Landkreis A unterstützen, im Vergleich zu dem Anteil, der das Gesetz in Landkreis B befürwortet, schätzen. Hier sind die zusammenfassenden Daten für jede Stichprobe:

Beispiel 1:

• n ₁ = 100
• p ₁ = 0,62 (d.h. 62 von 100 Einwohnern unterstützen das Gesetz)

Probe 2:

• n ₂ = 100
• p ₂ = 0,46 (d.h. 46 unserer 100 Einwohner unterstützen das Gesetz)

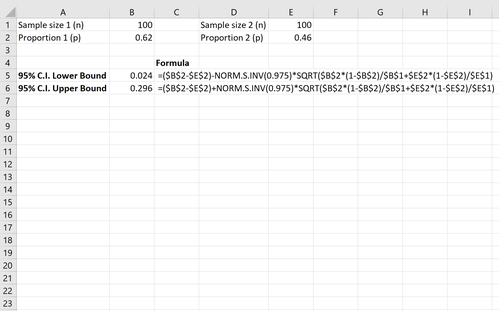
Der folgende Screenshot zeigt, wie ein 95%-Konfidenzintervall für den wahren Unterschied im Anteil der Einwohner, die das Gesetz unterstützen, zwischen den Landkreisen berechnet wird:

Das 9-5%-Konfidenzintervall für den wahren Unterschied des Anteils der Einwohner, die das Gesetz unterstützen, zwischen den Landkreisen beträgt [0,024, 0,296].

Weitere Excel-Tutorials finden Sie hier.