So berechnen Sie die gewichtete Standardabweichung in Python

Die gewichtete Standardabweichung ist eine nützliche Methode, um die Streuung von Werten in einem Datensatz zu messen, wenn einige Werte im Datensatz höhere Gewichtungen als andere haben.

Die Formel zur Berechnung einer gewichteten Standardabweichung lautet:

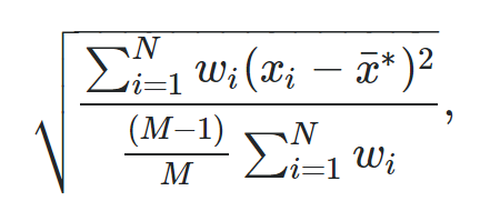
wo:

• N: Die Gesamtzahl der Beobachtungen
• M: Die Anzahl der Nicht-Null-Gewichtungen
• w _i : Ein Vektor von Gewichten
• x _i : Ein Vektor von Datenwerten
• x : Der gewichtete Mittelwert

Der einfachste Weg, eine gewichtete Standardabweichung in Python zu berechnen, ist die Verwendung der Funktion DescrStatsW() aus dem Paket statsmodels:

DescrStatsW(values, weights=weights, ddof=1).std

Das folgende Beispiel zeigt, wie Sie diese Funktion in der Praxis verwenden.

Beispiel: Gewichtete Standardabweichung in Python

Angenommen, wir haben das folgende Array von Datenwerten und entsprechenden Gewichtungen:

#Datenwerte definieren 
values = [14, 19, 22, 25, 29, 31, 31, 38, 40, 41]

#gewichte definieren
weights = [1, 1, 1.5, 2, 2, 1.5, 1, 2, 3, 2]

Der folgende Code zeigt, wie die gewichtete Standardabweichung für dieses Array von Datenwerten berechnet wird:

from statsmodels.stats.weightstats import DescrStatsW

#Gewichtete Standardabweichung berechnen
DescrStatsW(values, weights=weights, ddof=1).std

8.570050878426773

Die gewichtete Standardabweichung ergibt sich zu 8,57.

Beachten Sie, dass wir auch var verwenden können, um die gewichtete Varianz schnell zu berechnen:

from statsmodels.stats.weightstats import DescrStatsW

#Gewichtete Varianz berechnen
DescrStatsW(values, weights=weights, ddof=1).var

73.44577205882352

Die gewichtete Varianz ergibt sich zu 73,446.

Zusätzliche Ressourcen

Die folgenden Tutorials erläutern, wie die gewichtete Standardabweichung in anderer Statistiksoftware berechnet wird:

So berechnen Sie die gewichtete Standardabweichung in Excel
So berechnen Sie die gewichtete Standardabweichung in R