Eine Einführung in die geometrische Verteilung

Die geometrische Verteilung beschreibt die Wahrscheinlichkeit, dass eine bestimmte Anzahl von Fehlern auftritt, bevor der erste Erfolg in einer Reihe von Bernoulli-Versuchen erzielt wird.

Eine Bernoulli-Studie ist ein Experiment mit nur zwei möglichen Ergebnissen – „Erfolg“ oder „Misserfolg“ – und die Erfolgswahrscheinlichkeit ist bei jeder Durchführung des Experiments gleich.

Ein Beispiel für einen Bernoulli-Prozess ist ein Münzwurf. Die Münze kann nur auf zwei Seiten landen (wir könnten Köpfe als „Erfolg“ und Schwänze als „Misserfolg“ bezeichnen) und die Erfolgswahrscheinlichkeit bei jedem Wurf beträgt 0,5, vorausgesetzt, die Münze ist fair.

Wenn eine Zufallsvariable X einer geometrischen Verteilung folgt, kann die Wahrscheinlichkeit, dass k Fehler auftreten, bevor der erste Erfolg auftritt, durch die folgende Formel ermittelt werden:

P(X = k) = (1-p) ^k p

wobei:

• k: Anzahl der Fehler vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

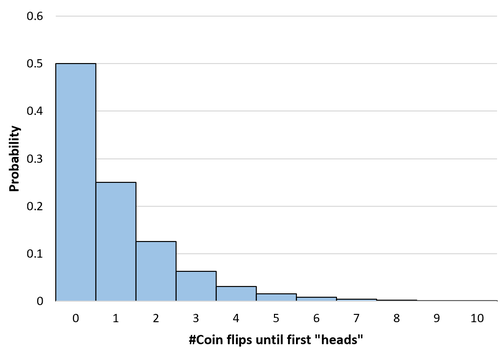
Nehmen wir zum Beispiel an, wir möchten wissen, wie oft wir eine faire Münze werfen müssen, bis sie auf den Köpfen landet. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, dass 0, 1, 2, 3 Fehler usw. auftreten, bevor die Münze auf den Köpfen landet:

Hinweis: Die Münze kann 0 „Fehler“ aufweisen, wenn sie beim ersten Wurf auf den Köpfen landet.

P(X = 0) = (1 – 0,5) ⁰ (0,5) = 0,5

P(X = 1) = (1 – 0,5) ¹ (0,5) = 0,25

P(X = 2) = (1 – 0,5) ² (0,5) = 0,125

P(X = 3) = (1 – 0,5) ³ (0,5) = 0,0625

Wir können die Wahrscheinlichkeit für eine beliebige Anzahl von Münzwürfen bis unendlich berechnen. Wir erstellen dann ein einfaches Histogramm, um diese Wahrscheinlichkeitsverteilung zu visualisieren:

Berechnung der kumulativen geometrischen Wahrscheinlichkeiten

Die kumulative Wahrscheinlichkeit, dass bis zum ersten Erfolg k oder weniger Fehler auftreten, kann durch die folgende Formel ermittelt werden:

P(X ≤ k) = 1 – (1-p) ^{k + 1}

wobei:

• k: Anzahl der Fehler vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

Angenommen, wir möchten wissen, mit welcher Wahrscheinlichkeit drei oder weniger „Fehler“ auftreten, bis die Münze schließlich auf den Köpfen landet. Wir würden die folgende Formel verwenden, um diese Wahrscheinlichkeit zu berechnen:

P(X ≤ 3) = 1 – (1 – 0,5) ^{3 + 1} = 0,9375

Wir können jede kumulative Wahrscheinlichkeit mit einer ähnlichen Formel berechnen:

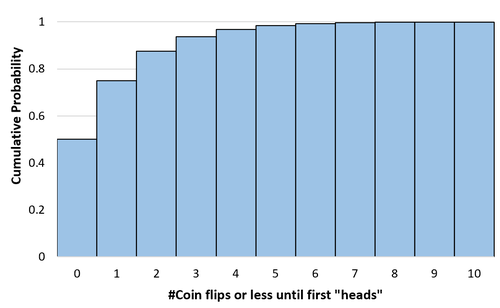
P(X ≤ 0) = 1 – (1 – 0,5) ^{0 + 1} = 0,5

P(X ≤ 1 ) = 1 – (1 – 0,5) ^{1 + 1} = 0,75

P(X ≤ 2) = 1 – (1 – 0,5) ^{2 + 1} = 0,875

Wir können diese kumulativen Wahrscheinlichkeiten für eine beliebige Anzahl von Münzwürfen bis unendlich berechnen. Wir können dann ein Histogramm erstellen, um diese kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

Eigenschaften der geometrischen Verteilung

Die geometrische Verteilung hat folgende Eigenschaften:

Der Mittelwert der Verteilung beträgt (1-p) / p.

Die Varianz der Verteilung beträgt (1-p) / p ².

Beispielsweise:

Die durchschnittliche Häufigkeit, mit der wir erwarten würden, dass eine Münze auf Schwänzen landet, bevor sie auf Köpfen landet, ist (1-p) / p = (1-.5) / .5 = 1.

Die Varianz in der Anzahl der Flips bis zur Landung auf den Köpfen wäre (1-p) / p ² = (1-.5) / .5 ² = 2.

Probleme mit der geometrischen Verteilungspraxis

Verwenden Sie die folgenden Übungsprobleme, um Ihr Wissen über die geometrische Verteilung zu testen.

Problem 1

Frage: Ein Forscher wartet außerhalb einer Bibliothek, um Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie hoch ist die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, die erste Person ist, die das Gesetz unterstützt?

Antwort: Die Anzahl der „Fehler“ bis zum ersten Erfolg –d.h.die Anzahl der Personen, die das Gesetz erst unterstützen, wenn die erste Person es unterstützt – beträgt 3. Verwenden Sie daher den Geometric Distribution Calculator mit p = 0,2 und x = 3 Fehler finden wir, dass P(X = 3) = 0,10240.

Problem 2

Frage: Ein Forscher wartet außerhalb einer Bibliothek, um Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie hoch ist die Wahrscheinlichkeit, dass der Forscher mit mehr als vier Personen sprechen muss, um jemanden zu finden, der das Gesetz unterstützt?

Antwort: Unter Verwendung des geometrischen Verteilungsrechners mit p = 0,2 und x = 4 Fehlern stellen wir fest, dass P(X> 4) = 0,32768 ist.

Problem 3

Frage: Ein Forscher wartet außerhalb einer Bibliothek, um Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Mit wie vielen Personen muss die Forscherin voraussichtlich sprechen, bis sie jemanden findet, der das Gesetz unterstützt?

Antwort: Denken Sie daran, dass der Mittelwert der geometrischen Verteilung (1-p) / p ist. In dieser Situation wäre der Mittelwert (1 – 0,2) / 0,2 = 4.