Lineare Regression in Excel – so geht’s

Die einfache lineare Regression (auch lineare Einfachregression) ist eine Methode, mit der wir die Beziehung zwischen einer erklärenden Variablen x und einer Antwortvariablen y verstehen können.
In diesem Tutorial wird erklärt, wie Sie eine lineare Einfachregression in Excel durchführen.

Beispiel: einfache lineare Regression in Excel

Angenommen, wir möchten die Beziehung zwischen der Anzahl der Stunden, die ein Student für eine Prüfung studiert, und der Prüfungsnote, die er erhält, verstehen. Um diese Beziehung zu untersuchen, können wir eine einfache lineare Regression durchführen, indem wir die Lern-Stunden als erklärende Variable und die Prüfungsergebnisse als Antwortvariable verwenden.

Führen Sie die folgenden Schritte in Excel aus, um eine einfache lineare Regression durchzuführen.

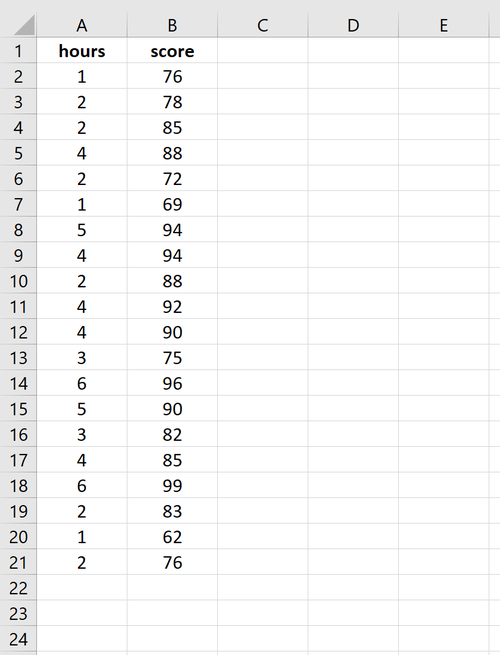
Schritt 1: Geben Sie die Daten ein.

Geben Sie die folgenden Daten für die Anzahl der Stunden und die Prüfungsergebnisse für 20 Schüler ein:

Schritt 2: Visualisieren Sie die Daten.

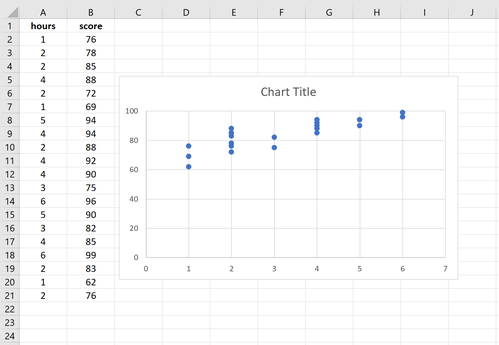
Bevor wir eine einfache lineare Regression durchführen, ist es hilfreich, ein Streudiagramm der Daten zu erstellen, um sicherzustellen, dass tatsächlich eine lineare Beziehung zwischen den untersuchten Stunden und dem Prüfungsergebnis besteht.

Markieren Sie die Daten in den Spalten A und B. Wechseln Sie entlang der oberen Multifunktionsleiste in Excel zur Registerkarte Einfügen. Klicken Sie in der Gruppe Diagramme auf Punkt(X, Y) und klicken Sie auf die erste Option mit dem Titel Punkt(X, Y). Dadurch wird automatisch das folgende Streudiagramm erstellt:

Die Anzahl der untersuchten Stunden wird auf der x-Achse und die Prüfungsergebnisse auf der y-Achse angezeigt. Wir können sehen, dass es eine lineare Beziehung zwischen den beiden Variablen gibt – mehr untersuchte Stunden sind mit höheren Prüfungsergebnissen verbunden.

Um die Beziehung zwischen diesen beiden Variablen zu quantifizieren, können wir eine einfache lineare Regression durchführen.

Schritt 3: Führen Sie eine einfache lineare Regression durch.

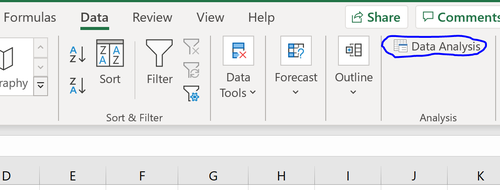
Wechseln Sie in Excel im oberen Menüband zur Registerkarte Daten und klicken Sie auf Datenanalyse. Wenn diese Option nicht angezeigt wird, müssen Sie zuerst das kostenlose Analysis ToolPak installieren.

Sobald Sie auf Datenanalyse klicken, wird ein neues Fenster geöffnet. Wählen Sie Regression und klicken Sie auf OK.

Geben Sie für den Eingabe-Y-Bereich das Wertearray für die Antwortvariable ein. Geben Sie für den Eingabe-X-Bereich das Wertearray für die erklärende Variable ein. Aktivieren Sie das Kontrollkästchen neben Beschriftungen, damit Excel weiß, dass wir die Variablennamen in die Eingabebereiche aufgenommen haben. Wählen Sie als Ausgabebereich eine Zelle aus, in der die Ausgabe der Regression angezeigt werden soll. Klicken Sie dann auf OK.

Die folgende Ausgabe wird automatisch angezeigt:

Schritt 4: Interpretieren Sie die Ausgabe.

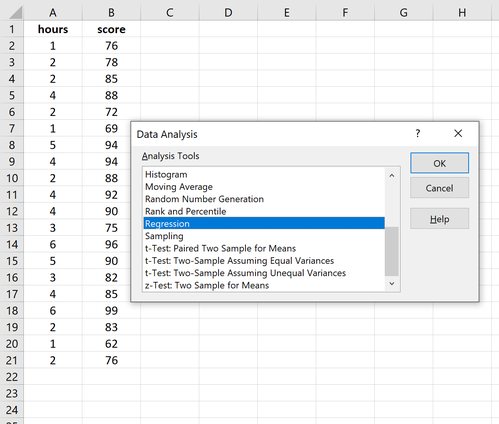
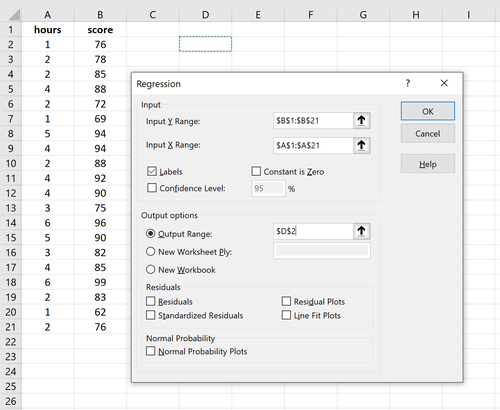
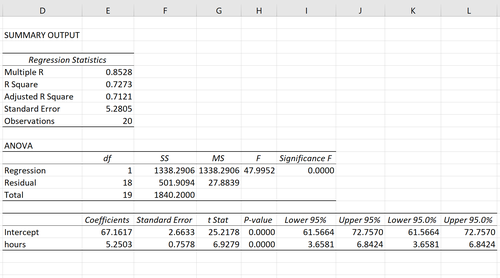
So interpretieren Sie die relevantesten Zahlen in der Ausgabe:

R Square: 0,7273. Dies ist als Bestimmungskoeffizient bekannt. Es ist der Anteil der Varianz in der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können 72,73% der Abweichungen in den Prüfungsergebnissen durch die Anzahl der untersuchten Stunden erklärt werden.

Standard Error: 5.2805. Dies ist der durchschnittliche Abstand, um den die beobachteten Werte von der Regressionslinie fallen. In diesem Beispiel fallen die beobachteten Werte durchschnittlich um 5,2805 Einheiten von der Regressionslinie ab.

F: 47,9952. Dies ist die Gesamt-F-Statistik für das Regressionsmodell, berechnet als Regressions-MS / Residuen-MS.

Significance F: 0,0000. Dies ist der p-Wert, der der gesamten F-Statistik zugeordnet ist. Es zeigt uns, ob das Regressionsmodell statistisch signifikant ist oder nicht. Mit anderen Worten, es sagt uns, ob die erklärende Variable eine statistisch signifikante Assoziation mit der Antwortvariablen hat. In diesem Fall beträgt der p-Wert weniger als 0,05, was darauf hinweist, dass ein statistisch signifikanter Zusammenhang zwischen den untersuchten Stunden und dem erhaltenen Prüfungsergebnis besteht.

Coefficients: Die Koeffizienten geben uns die Zahlen an, die zum Schreiben der geschätzten Regressionsgleichung erforderlich sind. In diesem Beispiel lautet die geschätzte Regressionsgleichung:

exam score = 67,16 + 5,2503 * (hours)

Wir interpretieren den Koeffizienten für Stunden so, dass für jede weitere untersuchte Stunde die Prüfungspunktzahl im Durchschnitt um 5,2503 steigt. Wir interpretieren den Koeffizienten für den Achsenabschnitt so, dass die erwartete Prüfungspunktzahl für einen Studenten, der null Stunden studiert, 67,16 beträgt.

Wir können diese geschätzte Regressionsgleichung verwenden, um die erwartete Prüfungspunktzahl für einen Schüler basierend auf der Anzahl der Stunden zu berechnen, die er studiert. Zum Beispiel wird von einem Studenten, der drei Stunden studiert, erwartet, dass er eine Prüfungsnote von 82,91 erhält:

exam score = 67,16 + 5,2503 * (3) = 82,91