So verwenden Sie den Dunnett-Test für mehrere Vergleiche

Eine ANOVA wird verwendet, um zu bestimmen, ob es einen statistisch signifikanten Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen gibt oder nicht.

Wenn der p-Wert aus der ANOVA kleiner als ein gewähltes Signifikanzniveau ist, können wir die Nullhypothese verwerfen und schlussfolgern, dass wir genügend Beweise haben, um zu sagen, dass sich mindestens einer der Mittelwerte der Gruppen von den anderen unterscheidet.

Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Es sagt uns einfach, dass nicht alle Gruppenmittel gleich sind. Um genau herauszufinden, welche Gruppen sich voneinander unterscheiden, müssen wir einen Post-hoc-Test durchführen.

Wenn eine der Gruppen in der Studie als Kontrollgruppe betrachtet wird, sollten wir den Dunnett-Test als Post-hoc-Test nach der ANOVA verwenden.

Dunnett-Test: Definition

Wir können die folgenden zwei Schritte verwenden, um den Dunnett-Test durchzuführen:

Schritt 1: Finden Sie den kritischen Wert von Dunnett.

Zuerst müssen wir den kritischen Wert von Dunnett ermitteln. Dies wird wie folgt berechnet:

Kritischer Wert nach Dunnett: t _d √ 2MS _w /n

wo:

• t _d: Der in der Dunnett-Tabelle gefundene Wert für eine gegebene Alpha-Stufe, Gruppenanzahl und Gruppenstichprobengröße.
• MS _w: Die mittleren Quadrate der „innerhalb der Gruppe“ in der ANOVA-Ausgabetabelle
• n: Die Größe der Gruppenstichproben

Schritt 2: Vergleichen Sie die Differenzen der Gruppenmittelwerte mit dem kritischen Wert von Dunnett.

Als nächstes berechnen wir die absolute Differenz zwischen dem Mittelwert jeder Gruppe und dem Mittelwert der Kontrollgruppe. Wenn der Unterschied den kritischen Wert von Dunnett überschreitet, wird dieser Unterschied als statistisch signifikant bezeichnet.

Das folgende Beispiel zeigt, wie der Dunnett-Test in der Praxis durchgeführt wird.

Dunnett-Test: Beispiel

Angenommen, eine Lehrkraft möchte wissen, ob zwei neue Lerntechniken das Potenzial haben, die Prüfungsergebnisse ihrer Schüler zu verbessern. Um dies zu testen, teilt sie ihre 30-köpfige Klasse nach dem Zufallsprinzip in die folgenden drei Gruppen ein:

• Kontrollgruppe: 10 Schüler
• Neue Lerntechnik 1: 10 Schüler
• Neue Lerntechnik 2: 10 Schüler

Nach einer Woche mit der ihm zugewiesenen Lerntechnik legt jeder Schüler dieselbe Prüfung ab. Die Ergebnisse sind wie folgt:

• Mittleres Prüfungsergebnis der Kontrollgruppe: 81,6
• Durchschnittliche Prüfungsnote der neuen Lerntechnik 1 Gruppe: 85,8
• Durchschnittliche Prüfungsnote der neuen Lerntechnik 2 Gruppe: 87,7
• Mittlere Quadrate der „innerhalb der Gruppe“ in der ANOVA-Ausgabetabelle: 23,3

Anhand dieser Informationen können wir den Dunnett-Test durchführen, um festzustellen, ob eine der beiden neuen Studientechniken im Vergleich zur Kontrollgruppe signifikant unterschiedliche durchschnittliche Prüfungsergebnisse liefert.

Schritt 1: Finden Sie den kritischen Wert von Dunnett.

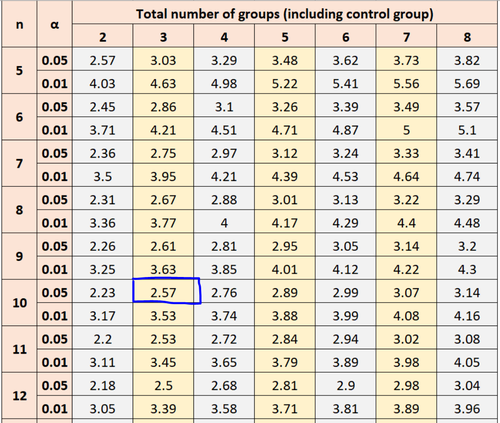
Unter Verwendung von α = 0,05, Gruppenstichprobengröße n = 10 und Gesamtgruppen = 3 sagt uns die Dunnett-Tabelle, einen Wert von 2,57 in der Berechnung des kritischen Werts zu verwenden.

Als nächstes können wir diese Zahl in die Formel einsetzen, um den kritischen Wert von Dunnett zu ermitteln:

Kritischer Wert nach Dunnett: t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548

Schritt 2: Vergleichen Sie die Differenzen der Gruppenmittelwerte mit dem kritischen Wert von Dunnett.

Der absolute Unterschied zwischen den Mittelwerten jeder Studientechnik und der Kontrollgruppe ist wie folgt:

• Abs. Differenz zwischen neuer Technik 1 und Kontrolle: |85,8 – 81,6| = 4,2
• Abs. Differenz zwischen neuer Technik 2 und Kontrolle: |87,7 – 81,6| = 6,1

Nur der absolute Unterschied zwischen Technik 2 und der Kontrollgruppe ist größer als Dunnetts kritischer Wert von 5,548.

Somit können wir sagen, dass die neue Lerntechnik Nr. 2 im Vergleich zur Kontrollgruppe signifikant andere Prüfungsergebnisse liefert, die neue Lerntechnik Nr. 1 jedoch nicht.

Zusätzliche Ressourcen

Eine Einführung in die einfaktorielle ANOVA
Eine Anleitung zur Verwendung von Post-Hoc-Tests mit ANOVA
So führen Sie den Dunnett-Test in R durch