Dispersionsmaße: Definition & Beispiele

Wenn wir einen Datensatz analysieren, kümmern wir uns oft um zwei Dinge:

1. Wo sich der Mittelwert befindet. Wir messen das „Zentrum“ oft anhand des Mittelwerts und des Medians.

2. Wie „verteilt“ die Werte sind. Wir messen die Streuung anhand der Spannweite, des Interquartilsabstands, der Varianz und der Standardabweichung.

Spannweite

Die Spannweite ist die Differenz zwischen dem größten und dem kleinsten Wert in einem Datensatz.

Angenommen, wir haben diesen Datensatz mit den Ergebnissen der endgültigen Mathematikprüfung für 20 Schüler:

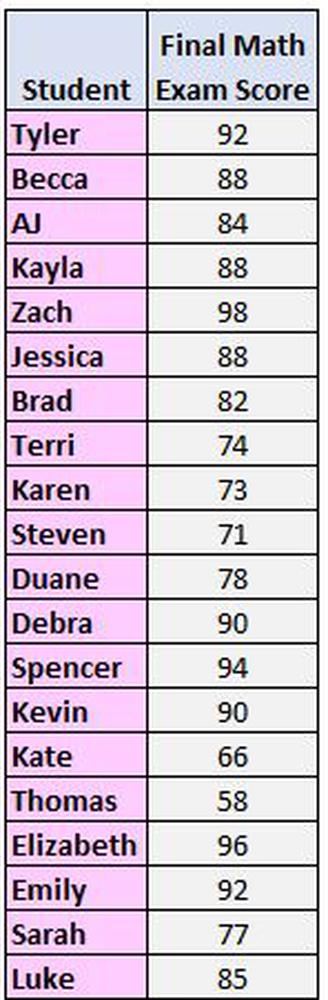
Der größte Wert ist 98. Der kleinste Wert ist 58. Somit liegt der Bereich zwischen 98 und 58 = 40.

Interquartilsabstand

Der Interquartilsabstand ist die Differenz zwischen dem ersten und dem dritten Quartil in einem Datensatz.

Quartile sind Werte, die einen Datensatz in vier gleiche Teile aufteilen. So ermitteln Sie den Interquartilsabstand des folgenden Datensatzes mit Prüfungsergebnissen:

1. Ordnen Sie die Werte vom kleinsten zum größten.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Finden Sie den Median. (In diesem Fall ist es der Durchschnitt der beiden mittleren Werte)

58, 66, 71, 73, 74, 77, 78, 82, 84, 85 (MEDIAN) 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

3. Der Median teilt den Datensatz in zwei Hälften. Der Median der unteren Hälfte ist das untere Quartil (Q1) und der Median der oberen Hälfte ist das obere Quartil (Q3)

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Der Interquartilsabstand ist gleich Q3 – Q1.

In diesem Fall ist Q1 der Durchschnitt der beiden mittleren Werte in der unteren Hälfte des Datensatzes (75,5) und Q3 der Durchschnitt der beiden mittleren Werte in der oberen Hälfte des Datensatzes (91).

Somit liegt der Interquartilsabstand zwischen 91 und 75,5 = 15,5

Interquartilsabstand vs. Spannweite

Der Interquartilsabstand ist im Vergleich zur Spannweite widerstandsfähiger gegen Ausreißer, was es zu einer besseren Metrik für die Messung der „Streuung“ machen kann.

Angenommen, wir haben den folgenden Datensatz mit Einkommen für zehn Personen:

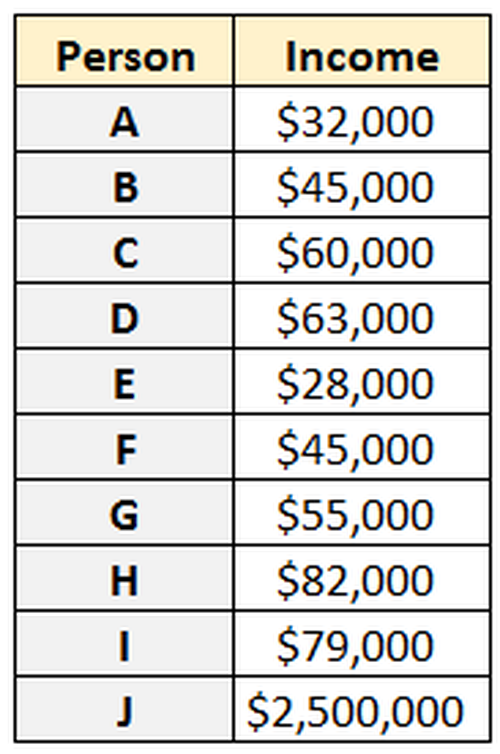
Die Spannweite beträgt 2.468.000 USD, aber der Interquartilsabstand beträgt 34.000 USD, was ein viel besserer Hinweis darauf ist, wie verteilt die Einkommen tatsächlich sind.

In diesem Fall führt das Ausreißereinkommen von Person J dazu, dass der Bereich extrem groß ist, und macht ihn zu einem schlechten Indikator für die „Streuung“ dieser Einkommen.

Varianz

Die Varianz ist eine gebräuchliche Methode, um die Verteilung der Datenwerte zu messen.

Die Formel zum Ermitteln der Varianz einer Population (bezeichnet als σ ² ) lautet:

σ ² = Σ (x _i – μ) ² / N.

Dabei ist μ der Populationsmittelwert, x _i das i- te Element aus der Population, N die Populationsgröße und Σ nur ein ausgefallenes Symbol, das „Summe“ bedeutet.

Normalerweise arbeiten wir mit Proben, nicht mit Populationen. Und die Formel zum Ermitteln der Varianz einer Stichprobe (bezeichnet als s ² ) lautet:

s ² = Σ (x _i – μ) ² / (n – 1)

Standardabweichung

Die Standardabweichung ist die Quadratwurzel der Varianz. Dies ist die gebräuchlichste Methode, um zu messen, wie verteilt Datenwerte sind.

Die Formel zum Ermitteln der Standardabweichung einer Population (bezeichnet als σ ) lautet:

√ Σ (x _i – μ) ² / N.

Die Formel zum Ermitteln der Standardabweichung einer Stichprobe (mit s bezeichnet ) lautet:

√Σ (x _i – μ) ² / (n-1)