So berechnen Sie Cohens d in Excel

Wenn wir in der Statistik feststellen möchten, ob zwischen zwei Gruppen ein signifikanter Unterschied besteht oder nicht, führen wir häufig einen Hypothesentest durch, der zu einem p-Wert führt. Wenn dieser p-Wert unter einem bestimmten Signifikanzniveau liegt (übliche Auswahlmöglichkeiten sind 0,10, 0,05 und 0,01), schließen wir daraus, dass zwischen den beiden Gruppen ein statistisch signifikanter Unterschied besteht.

Während ein p-Wert uns sagen kann, ob es einen statistisch signifikanten Unterschied zwischen gibt oder nicht, kann eine Effektgröße uns sagen, wie groß dieser Unterschied tatsächlich ist.

Eine der häufigsten Messungen der Effektgröße ist Cohens d, das wie folgt berechnet wird:

Cohens d = ( x ₁ – x ₂ ) / zusammengefasste SD

wo:

• x ₁ = Mittelwert der Gruppe 1
• x ₂ = Mittelwert der Gruppe 2
• zusammengefasste SD = √ ([(n ₁ -1) s ₁² + (n ₂ -1) s ₂² ] / [n ₁ + n ₂ – 2])

In diesem Tutorial wird erklärt, wie Sie Cohens d in Excel berechnen.

Beispiel: Cohens d in Excel

Führen Sie die folgenden Schritte aus, um Cohens d in Excel zu berechnen.

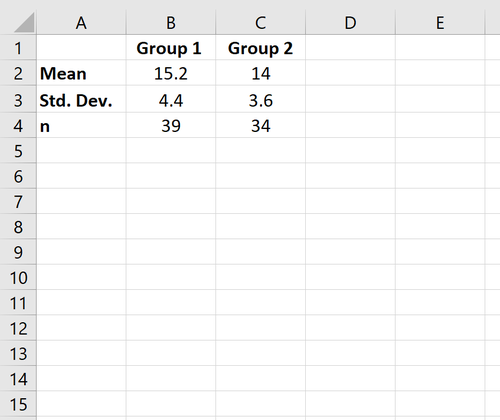
Schritt 1: Geben Sie die Daten ein.

Zuerst geben wir die Werte für Mittelwert, Standardabweichung und Stichprobengröße (n) für zwei Gruppen ein.

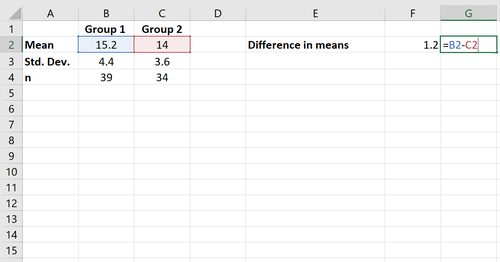
Schritt 2: Berechnen Sie die Differenz der Mittelwerte.

Als nächstes berechnen wir die Differenz zwischen den Gruppenmitteln.

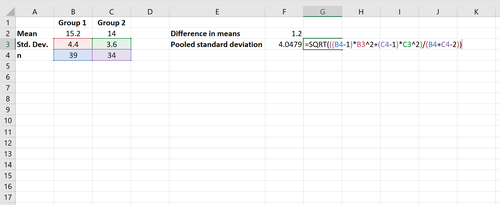
Schritt 3: Berechnen Sie die zusammengefasste Standardabweichung.

Als nächstes berechnen wir die zusammengefasste Standardabweichung.

(Die Formeln wurden mit einer englischsprachen Excel-Version erstellt. Für die deutschen Formeln siehe z.B. hier)

SQRT = WURZEL

Schritt 4: Berechnen Sie Cohens d.

Zuletzt berechnen wir Cohens d.

Cohens d ergibt für dieses Beispiel 0,2965.

Wie man Cohens d interpretiert

Als Faustregel gilt hier die Interpretation von Cohens d:

• 0,2 = Kleine Effektgröße
• 0,5 = Mittlere Effektgröße
• 0,8 = Große Effektgröße

In unserem Beispiel würde eine Effektgröße von 0,2965 wahrscheinlich als kleine Effektgröße angesehen. Dies bedeutet, dass selbst wenn der Unterschied zwischen den beiden Gruppenmitteln statistisch signifikant unterschiedlich ist, der tatsächliche Unterschied zwischen den Gruppenmitteln trivial ist.