So wenden Sie die 68–95–99.7 Regel in Excel an

Die 68–95–99.7 Regel (engl. auch empirical rule) besagt, dass für einen bestimmten Datensatz mit einer Normalverteilung folgendes gilt:

• 68% der Datenwerte liegen innerhalb einer Standardabweichung vom Mittelwert.
• 95% der Datenwerte liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• 99,7% der Datenwerte liegen innerhalb von drei Standardabweichungen vom Mittelwert.

In diesem Artikel wird erläutert, wie Sie die 68–95–99.7 Regel in Excel auf ein bestimmtes Dataset anwenden.

Anwenden der 68–95–99.7 Regel in Excel

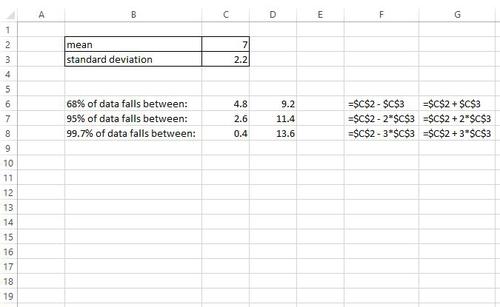
Angenommen, wir haben einen normalverteilten Datensatz mit einem Mittelwert von 7 und einer Standardabweichung von 2,2. Der folgende Screenshot zeigt, wie Sie die empirische Regel auf dieses Dataset in Excel anwenden, um festzustellen, zwischen welchen Werten 68% der Daten liegen, zwischen welchen Werten 95% der Daten liegen und zwischen welchen Werten 99,7% der Daten liegen:

Aus dieser Ausgabe können wir sehen:

• 68% der Daten liegen zwischen 4,8 und 9,2
• 95% der Daten liegen zwischen 2,6 und 11,4
• 99,7% der Daten liegen zwischen 0,4 und 13,6

Die Zellen in den Spalten F und G zeigen die Formeln, mit denen diese Werte ermittelt wurden.

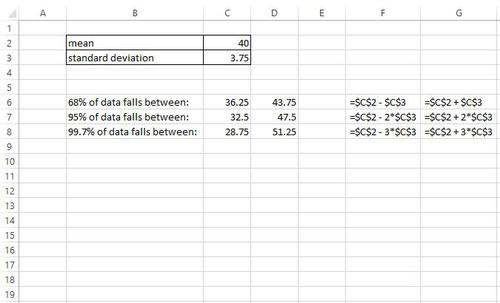
Um die empirische Regel auf einen anderen Datensatz anzuwenden, müssen wir lediglich den Mittelwert und die Standardabweichung in den Zellen C2 und C3 ändern. Hier erfahren Sie beispielsweise, wie Sie die empirische Regel auf einen Datensatz mit einem Mittelwert von 40 und einer Standardabweichung von 3,75 anwenden:

Aus dieser Ausgabe können wir sehen:

• 68% der Daten liegen zwischen 36,25 und 43,75
• 95% der Daten liegen zwischen 32,5 und 47,5
• 99,7% der Daten liegen zwischen 28,75 und 51,25

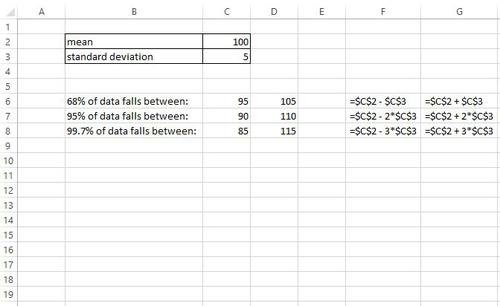
Und hier ist ein weiteres Beispiel für die Anwendung der empirischen Regel auf einen Datensatz mit einem Mittelwert von 100 und einer Standardabweichung von 5:

Aus dieser Ausgabe können wir sehen:

• 68% der Daten liegen zwischen 95 und 105
• 95% der Daten liegen zwischen 90 und 110
• 99,7% der Daten liegen zwischen 85 und 115

Finden, welcher Prozentsatz der Daten zwischen bestimmten Werten liegt

Eine andere Frage, die Sie möglicherweise haben, lautet: Wie viel Prozent der Daten liegen zwischen bestimmten Werten?

Angenommen, Sie haben einen normalverteilten Datensatz mit einem Mittelwert von 100 und einer Standardabweichung von 5 und möchten wissen, wie viel Prozent der Daten zwischen den Werten 99 und 105 liegen.

In Excel können wir diese Frage einfach mit der Funktion = NORM.VERT() beantworten, die die folgenden Argumente akzeptiert:

NORM.VERT(x, Mittelwert, Standardabwn, Kumuliert)

wo:

• x ist der Wert, an dem wir interessiert sind
• Mittelwert ist der Mittelwert der Verteilung
• Standardabwn ist die Standardabweichung der Verteilung
• Kumuliert nimmt den Wert „WAR“ (gibt die CDF zurück) oder „FALSCH“ (gibt das PDF zurück) an – wir verwenden „WAHR“, um den Wert der kumlierten Verteilungsfunktion zu erhalten.

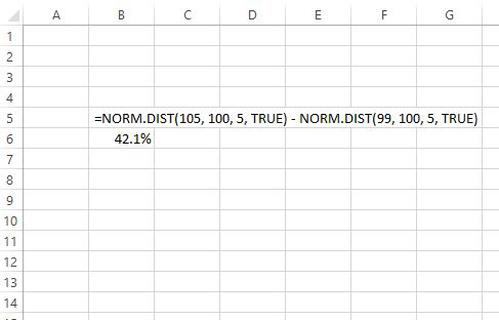
Der folgende Screenshot zeigt, wie Sie mit der Funktion NORM.VERT() den Prozentsatz der Daten ermitteln, der zwischen den Werten 99 und 105 für eine Verteilung mit einem Mittelwert von 100 und einer Standardabweichung von 5 liegt:

Wir sehen, dass 42,1% der Daten für diese Verteilung zwischen den Werten 105 und 99 liegen.