Zentraler Grenzwertsatz: Definition + Beispiele

Der zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts ungefähr normal ist, wenn die Stichprobengröße groß genug ist, auch wenn die Bevölkerung nicht normalverteilt ist.

Der zentrale Grenzwertsatz besagt auch, dass die Stichprobenverteilung die folgenden Eigenschaften hat:

1. Der Mittelwert der Stichprobenverteilung entspricht dem Mittelwert der Bevölkerungsverteilung:

x = μ

2. Die Varianz der Stichprobenverteilung entspricht der Varianz der Bevölkerungsverteilung geteilt durch die Stichprobengröße:

s² = σ² / n

Beispiele für den zentralen Grenzwertsatz

Hier einige Beispiele zur Veranschaulichung des zentralen Grenzwertsatzes in der Praxis.

Die Gleichverteilung

Angenommen, die Breite eines Schildkrötenpanzers folgt einer gleichmäßigen Verteilung mit einer minimalen Breite von 2 Zoll und einer maximalen Breite von 6 Zoll. Das heißt, wenn wir eine Schildkröte zufällig ausgewählt und die Breite ihrer Schale gemessen haben, ist es ebenso wahrscheinlich, dass sie irgendeine Breite zwischen 2 und 6 Zoll hat.

Wenn wir ein Histogramm erstellen würden, um die Verteilung der Schildkrötenpanzerbreiten darzustellen, würde es folgendermaßen aussehen:

Der Mittelwert einer Gleichverteilung ist μ = (b+a) / 2 wobei b der größtmögliche Wert und a der kleinstmögliche Wert ist. In diesem Fall ist es (6+2) / 2 = 4.

Die Varianz einer Gleichverteilung beträgt σ² = (b-a)² / 12. In diesem Fall ist sie (6-2)² / 12 = 1.33

Zufallsstichproben von 2 aus der Gleichverteilung

Stellen Sie sich dann vor, wir nehmen eine weitere Zufallsstichprobe von 2 Schildkröten aus dieser Population und messen erneut die Breite jeder Schildkrötenpanzer. Angenommen, das erste Schildkrötenpanzer hat eine Breite von 2,5 Zoll und das zweite hat ebenfalls eine Breite von 2,5 Zoll. Die mittlere Breite für diese Stichprobe von 2 Schildkröten beträgt 2,5 Zoll.

Stellen Sie sich vor, wir nehmen immer wieder zufällige Stichproben von 2 Schildkröten und ermitteln jedes Mal die mittlere Schalenbreite.

Wenn wir ein Histogramm erstellen würden, um die mittlere Schalenbreite all dieser Proben von 2 Schildkröten darzustellen, würde es so aussehen:

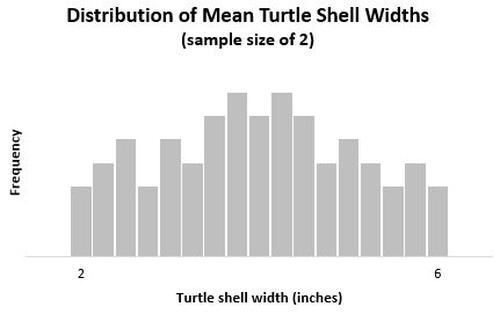
Dies ist als Stichprobenverteilung für den Stichprobenmittelwert bekannt, da hier die Verteilung der Stichprobenmittelwerte angezeigt wird.

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 4

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 1.33 / 2 = .665

Zufallsstichproben von 5 aus der Gleichverteilung

Stellen Sie sich nun vor, wir hätten dasselbe Experiment wiederholt, aber dieses Mal nehmen wir immer wieder zufällige Stichproben von 5 Schildkröten und ermitteln jedes Mal die mittlere Schalenbreite.

Wenn wir ein Histogramm erstellen würden, um die mittlere Schalenbreite all dieser Proben von 5 Schildkröten darzustellen, würde es so aussehen:

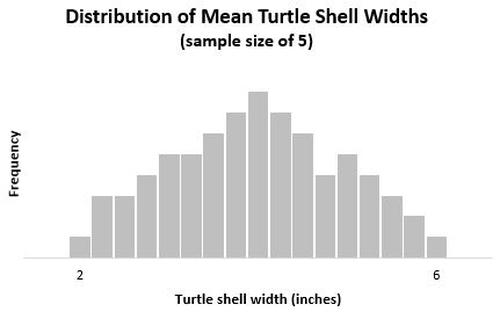
Beachten Sie, dass diese Verteilung eher eine „Glockenform“ hat, die der Normalverteilung ähnelt. Dies liegt daran, dass bei Stichproben von 5 die Varianz zwischen unseren Stichprobenmitteln viel geringer ist, sodass wir weniger wahrscheinlich Stichproben erhalten, bei denen der Mittelwert nahe 2 Zoll oder nahe 6 Zoll liegt, und eher Stichproben erhalten, bei denen die Mittelwert ist näher an der wahren Bevölkerung Mittelwert von 4 Zoll.

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 4

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 1.33 / 5 = .266

Entnahme von Zufallsstichproben von 30 aus der Gleichverteilung

Stellen Sie sich nun vor, wir hätten dasselbe Experiment wiederholt, aber dieses Mal nehmen wir immer wieder zufällige Stichproben von 30 Schildkröten und ermitteln jedes Mal die mittlere Schalenbreite.

Wenn wir ein Histogramm erstellen würden, um die mittlere Schalenbreite all dieser Proben von 30 Schildkröten darzustellen, würde es so aussehen:

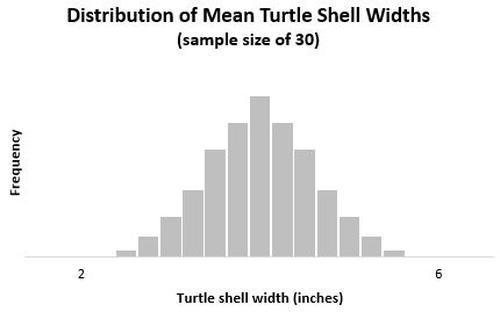
Beachten Sie, dass diese Stichprobenverteilung noch mehr Glockenform hat und viel schmaler ist als die beiden vorherigen Verteilungen.

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 4

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 1.33 / 30 = .044

Die Chi-Quadrat-Verteilung

Angenommen, die Anzahl der Haustiere pro Familie in einer bestimmten Stadt folgt einer Chi-Quadrat-Verteilung mit drei Freiheitsgraden. Wenn wir ein Histogramm erstellen würden, um die Verteilung der Haustiere pro Familie darzustellen, würde es folgendermaßen aussehen:

Der Mittelwert einer Chi-Quadrat-Verteilung ist einfach die Anzahl der Freiheitsgrade (df). In diesem Fall ist μ = 3.

Die Varianz einer Chi-Quadrat-Verteilung beträgt 2 * df. In diesem Fall ist σ² = 2 * 3 = 6.

Zufallsstichproben von 2

Stellen Sie sich vor, wir nehmen eine Zufallsstichprobe von 2 Familien aus dieser Population und zählen die Anzahl der Haustiere in jeder Familie. Angenommen, die erste Familie hat 4 Haustiere und die zweite Familie hat 1 Haustier. Die durchschnittliche Anzahl der Haustiere für diese Stichprobe von 2 Familien beträgt 2,5.

Stellen Sie sich dann vor, wir nehmen eine weitere Zufallsstichprobe von 2 Familien aus dieser Population und zählen erneut die Anzahl der Haustiere in jeder Familie. Angenommen, die erste Familie hat 6 Haustiere und die zweite Familie hat 4 Haustiere. Die durchschnittliche Anzahl der Haustiere für diese Stichprobe von 2 Familien beträgt 5.

Stellen Sie sich vor, wir nehmen immer wieder Zufallsstichproben von 2 Familien und ermitteln jedes Mal die durchschnittliche Anzahl der Haustiere.

Wenn wir ein Histogramm erstellen würden, um die mittlere Anzahl von Haustieren aller dieser Stichproben von 2 Familien darzustellen, würde es so aussehen:

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 3

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 6 / 2 = 3

Zufallsstichproben von 10

Stellen Sie sich nun vor, wir hätten dasselbe Experiment wiederholt, aber dieses Mal nehmen wir immer wieder Zufallsstichproben von 10 Familien und ermitteln jedes Mal die mittlere Anzahl von Haustieren pro Familie.

Wenn wir ein Histogramm erstellen würden, um die mittlere Anzahl von Haustieren pro Familie in all diesen Stichproben von 10 Familien darzustellen, würde es so aussehen:

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 3

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 6 / 10 = 0.6

Zufallsstichproben von 30

Stellen Sie sich nun vor, wir hätten dasselbe Experiment wiederholt, aber dieses Mal nehmen wir immer wieder Zufallsstichproben von 30 Familien und ermitteln jedes Mal die mittlere Anzahl von Haustieren pro Familie.

Wenn wir ein Histogramm erstellen würden, um die durchschnittliche Anzahl von Haustieren pro Familie in all diesen Stichproben von 30 Familien darzustellen, würde es so aussehen:

Der Mittelwert dieser Stichprobenverteilung ist x = μ = 3

Die Varianz dieser Stichprobenverteilung beträgt s² = σ² / n = 6 / 30 = 0.2

Zusammenfassung

Hier sind die wichtigsten Erkenntnisse aus diesen beiden Beispielen:

• Die Stichprobenverteilung eines Stichprobenmittelwerts ist ungefähr normal, wenn die Stichprobengröße groß genug ist, auch wenn die Bevölkerung nicht normalverteilt ist. In den beiden obigen Beispielen waren weder die gleichmäßige Verteilung noch die Chi-Quadrat-Verteilung normal (sie hatten überhaupt keine „Glockenform“), aber als wir eine ausreichend große Stichprobengröße nahmen, drehte sich die Verteilung des Stichprobenmittelwerts um normal zu sein.
• Je größer die Stichprobengröße ist, desto geringer ist die Varianz des Stichprobenmittelwerts.

„Groß genug“ definieren**

Es sei daran erinnert, dass der zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts ungefähr normal ist, wenn die Stichprobengröße „groß genug“ ist, auch wenn die Bevölkerungsverteilung nicht normal ist.

Es gibt keine genaue Definition dafür, wie groß eine Stichprobengröße sein muss, damit der zentrale Grenzwertsatz angewendet werden kann. Im Allgemeinen hängt dies jedoch von der Schiefe der Bevölkerungsverteilung ab, aus der die Stichprobe stammt:

• Wenn die Bevölkerungsverteilung symmetrisch ist, reicht manchmal eine Stichprobengröße von 4 oder 5 aus.
• Wenn die Bevölkerungsverteilung verzerrt ist, wird im Allgemeinen eine Stichprobengröße von mindestens 30 benötigt.
• Wenn die Bevölkerungsverteilung extrem verzerrt ist, kann eine Stichprobengröße von 40 oder höher erforderlich sein.