So fügen Sie einem Streudiagramm in Excel eine Regressionslinie hinzu

Eine einfache lineare Regressionslinie stellt die Linie dar, die am besten zu einem Datensatz passt.

Dieses Tutorial bietet ein schrittweises Beispiel dafür, wie Sie einem Streudiagramm in Excel schnell eine einfache lineare Regressionslinie hinzufügen.

Schritt 1: Erstellen Sie die Daten

Lassen Sie uns zunächst ein einfaches Dataset erstellen, mit dem Sie arbeiten können:

Schritt 2: Erstellen Sie ein Streudiagramm

Markieren Sie als Nächstes den Zellbereich A2:B21. Im oberen Menüband, klicken Sie auf Einfügen und dann auf Streudiagramm in der Charts-Gruppe und auf die erste Option, um ein Streudiagramm zu erstellen:

(Die Analyse im untenstehenden Bild wurden mit einer englischsprachen Excel-Version erstellt. In der deutschen Version können die Begriffe abweichen.)

Das folgende Streudiagramm wird angezeigt:

Schritt 3: Fügen Sie eine Regressionslinie hinzu

Klicken Sie anschließend auf eine beliebige Stelle im Streudiagramm. Klicken Sie dann auf das Pluszeichen (+) in der oberen rechten Ecke des Diagramms und aktivieren Sie das Kontrollkästchen Trendlinie.

Dadurch wird Ihrem Streudiagramm automatisch eine einfache lineare Regressionslinie hinzugefügt:

(Die Analyse im untenstehenden Bild wurden mit einer englischsprachen Excel-Version erstellt. In der deutschen Version können die Begriffe abweichen.)

Schritt 4: Fügen Sie eine Regressionsgeradengleichung hinzu

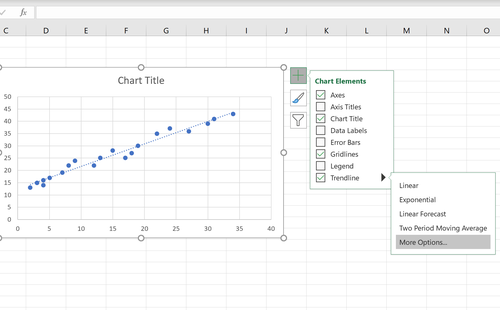
Sie können dem Diagramm auch die Gleichung der Regressionslinie hinzufügen, indem Sie auf Weitere Optionen klicken. Aktivieren Sie im rechts angezeigten Feld das Kontrollkästchen neben Gleichung im Diagramm anzeigen.

Die einfache lineare Regressionsgleichung wird automatisch im Streudiagramm angezeigt:

Für dieses spezielle Beispiel stellt sich die Regressionsgerade wie folgt heraus:

y = 0,917x + 12,462

Dies ist wie folgt zu interpretieren:

• Für jede zusätzliche Zunahme der x-Variable um eine Einheit beträgt die durchschnittliche Zunahme der y-Variable 0,917.
• Wenn die x-Variable gleich null ist, beträgt der Durchschnittswert für die y-Variable 12,462.

Wir können diese Gleichung auch verwenden, um den Wert von y basierend auf dem Wert von x zu schätzen. Wenn beispielsweise x gleich 15 ist, ist der erwartete Wert für y 26,217:

y = 0,917*(15) + 12,462 = 26,217

Weitere Excel-Tutorials finden Sie hier.