Was ist eine Stichprobenverteilung?

Stellen Sie sich vor, es gibt eine Population von 10.000 Delfinen und das Durchschnittsgewicht eines Delfins in dieser Population beträgt 300 Pfund.

Wenn wir eine einfache Zufallsstichprobe von 50 Delfinen aus dieser Population nehmen, stellen wir möglicherweise fest, dass das Durchschnittsgewicht der Delfine in dieser Stichprobe 305 Pfund beträgt.

Wenn wir dann eine weitere einfache Zufallsstichprobe von 50 Delfinen nehmen, stellen wir möglicherweise fest, dass das Durchschnittsgewicht der Delfine in dieser Stichprobe 295 Pfund beträgt.

Jedes Mal, wenn wir eine einfache Zufallsstichprobe von 50 Delfinen nehmen, ist es wahrscheinlich, dass das Durchschnittsgewicht der Delfine in der Stichprobe nahe am Bevölkerungsdurchschnitt von 300 Pfund liegt, aber nicht genau 300 Pfund.

Stellen Sie sich vor, wir nehmen 200 einfache Zufallsstichproben von 50 Delfinen aus dieser Population und erstellen ein Histogramm des Durchschnittsgewichts in jeder Stichprobe:

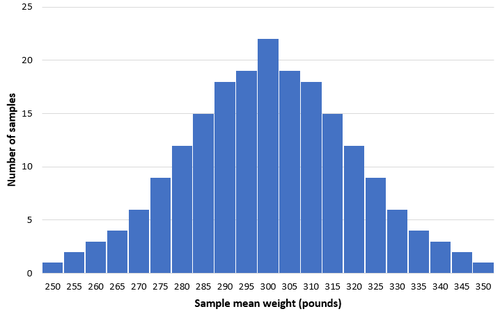
In den meisten Proben liegt das mittlere Gewicht nahe bei 300 Pfund. In seltenen Fällen können wir eine Probe voller kleiner Delfine auswählen, bei denen das Durchschnittsgewicht nur 250 Pfund beträgt. Oder wir pflücken zufällig eine Probe voller großer Delfine mit einem Durchschnittsgewicht von 350 Pfund. Im Allgemeinen ist die Verteilung der Stichprobenmittelwerte ungefähr normal, wobei sich das Verteilungszentrum im wahren Zentrum der Bevölkerung befindet.

Diese Verteilung der Stichprobenmittelwerte ist als Stichprobenverteilung des Mittelwerts bekannt und hat die folgenden Eigenschaften:

μ _x = μ

Dabei ist μ _x der Stichprobenmittelwert und μ der Populationsmittelwert.

σ _x = σ / √n

Dabei ist σ _x die Stichprobenstandardabweichung, σ die Populationsstandardabweichung und n die Stichprobengröße.

Zum Beispiel wissen wir in dieser Population von Delfinen, dass das mittlere Gewicht μ = 300 ist. Der Mittelwert der Stichprobenverteilung ist also μ _x = 300.

Angenommen, wir wissen auch, dass die Standardabweichung der Bevölkerung 18 Pfund beträgt. Die Standardabweichung der Stichprobe beträgt also σ _x = 18 / √50 = 2,546.

Stichprobenverteilung des Anteils

Betrachten Sie die gleiche Population von 10.000 Delfinen. Angenommen, 10% der Delfine sind schwarz und das Residuum ist grau. Angenommen, wir nehmen eine einfache Zufallsstichprobe von 50 Delfinen und stellen fest, dass 14% der Delfine in dieser Stichprobe schwarz sind. Dann nehmen wir eine weitere einfache Zufallsstichprobe von 50 Delfinen und stellen fest, dass 8% der Delfine in dieser Stichprobe schwarz sind.

Stellen Sie sich vor, wir nehmen 200 einfache Zufallsstichproben von 50 Delfinen aus dieser Population und erstellen ein Histogramm des Anteils der Delfine, die in jeder Stichprobe schwarz sind:

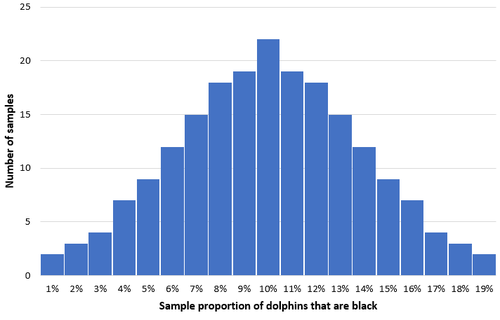
In den meisten Proben liegt der Anteil der schwarzen Delfine nahe an der tatsächlichen Population von 10%. Die Verteilung des Stichprobenanteils der schwarzen Delfine ist ungefähr normal, wobei sich das Verteilungszentrum im wahren Zentrum der Population befindet.

Diese Verteilung der Stichprobenanteile wird als Stichprobenverteilung des Anteils bezeichnet und hat folgende Eigenschaften:

μ _p = P.

Dabei ist p der Stichprobenanteil und P der Bevölkerungsanteil.

σ _p = √ (P) (1-P) / n

Dabei ist P der Bevölkerungsanteil und n die Stichprobengröße.

Zum Beispiel wissen wir in dieser Delfinpopulation, dass der wahre Anteil der schwarzen Delfine 10% = 0,1 beträgt. Der Mittelwert der Stichprobenverteilung des Anteils beträgt also μ _p = 0,1.

Angenommen, wir wissen auch, dass die Standardabweichung der Bevölkerung 18 Pfund beträgt. Die Standardabweichung der Stichprobe beträgt also σ _p = √ (P) (1-P) / n = √ (.1) (1-.1) / 50 = .042.