Was sind Residuen in der Statistik?

Ein Residuum ist die Differenz zwischen einem beobachteten Wert und einem vorhergesagten Wert in der Regressionsanalyse.

Es wird berechnet als:

Residuum = Beobachteter Wert – Vorhergesagter Wert

Denken Sie daran, dass das Ziel der linearen Regression darin besteht, die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu quantifizieren. Dazu findet die lineare Regression die Linie, die am besten zu den Daten passt, die als Regressionslinie der kleinsten Quadrate bekannt ist.

Diese Linie erzeugt eine Vorhersage für jede Beobachtung im Dataset, aber es ist unwahrscheinlich, dass die Vorhersage der Regressionslinie genau mit dem beobachteten Wert übereinstimmt.

Die Differenz zwischen der Vorhersage und dem beobachteten Wert ist das Residuum. Wenn wir die beobachteten Werte grafisch darstellen und die angepasste Regressionslinie überlagern, wären die Residuen für jede Beobachtung der vertikale Abstand zwischen der Beobachtung und der Regressionslinie:

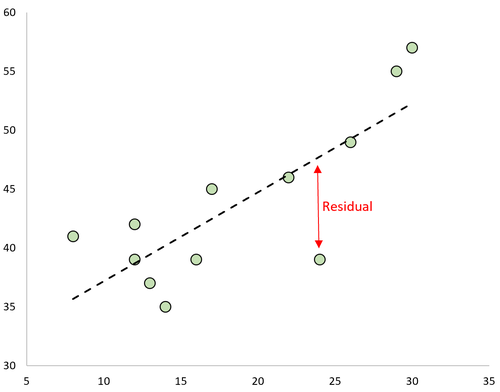
Eine Beobachtung hat ein positives Residuum, wenn ihr Wert größer ist als der vorhergesagte Wert der Regressionsgerade.

Umgekehrt hat eine Beobachtung ein negatives Residuum, wenn ihr Wert kleiner ist als der von der Regressionsgerade vorhergesagte Wert.

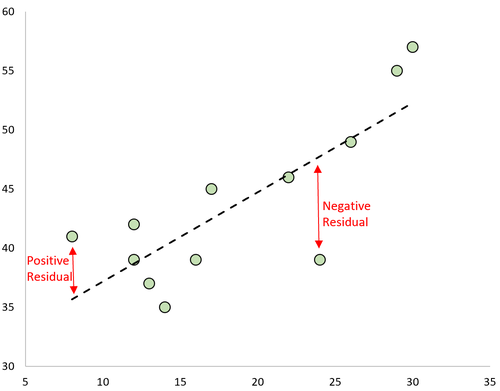
Einige Beobachtungen haben positive Residuen, während andere negative Residuen aufweisen, aber alle Residuen addieren sich zu Null.

Beispiel für die Berechnung von Residualwerten

Angenommen, wir haben den folgenden Datensatz mit insgesamt 12 Beobachtungen:

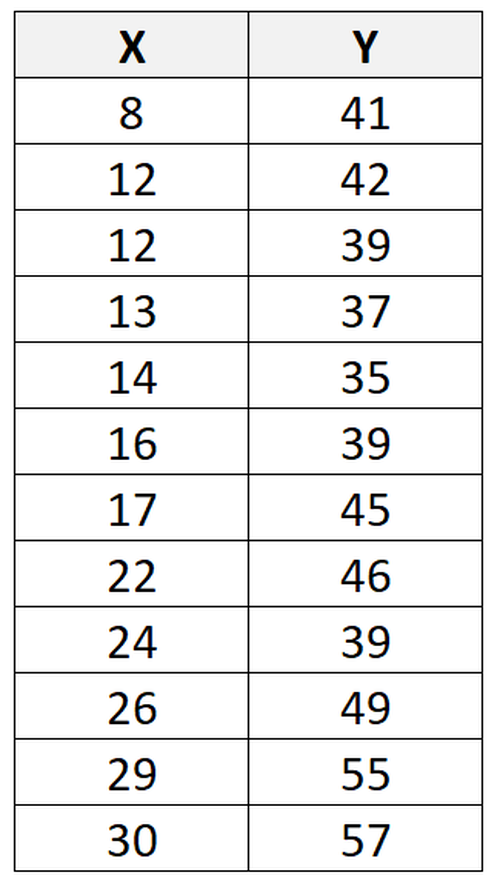
Wenn wir eine statistische Software (wie R, Excel, Python, Stata usw.) verwenden, um eine lineare Regressionslinie an diesen Datensatz anzupassen, werden wir feststellen, dass die Linie der besten Anpassung wie folgt lautet:

y = 29,63 + 0,7553x

Anhand dieser Linie können wir den vorhergesagten Wert für jeden Y-Wert basierend auf dem Wert von X berechnen. Der vorhergesagte Wert der ersten Beobachtung wäre beispielsweise:

y = 29,63 + 0,7553*(8) = 35,67

Wir können dann das Residuum für diese Beobachtung berechnen als:

Rest = Beobachteter Wert – Vorhergesagter Wert = 41 – 35,67 = 5,33

Wir können diesen Vorgang wiederholen, um das Residuum für jede einzelne Beobachtung zu finden:

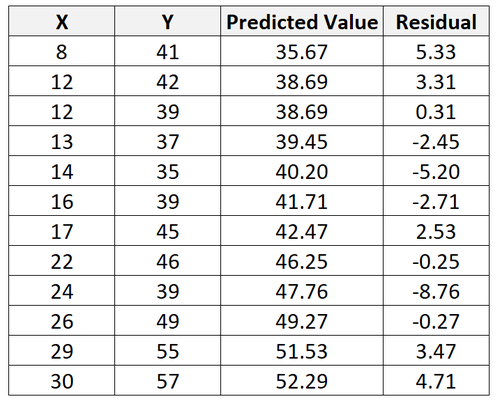
Wenn wir ein Streudiagramm erstellen, um die Beobachtungen zusammen mit der angepassten Regressionslinie zu visualisieren, sehen wir, dass einige der Beobachtungen oberhalb der Linie liegen, während andere unterhalb der Linie liegen:

Eigenschaften von Rückständen

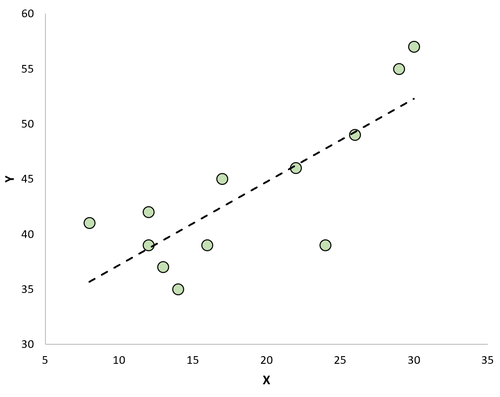
Reste haben folgende Eigenschaften:

• Jede Beobachtung in einem Datensatz hat ein entsprechendes Residuum. Wenn ein Datensatz also 100 Gesamtbeobachtungen enthält, erzeugt das Modell 100 vorhergesagte Werte, was zu 100 Gesamtresiduen führt.
• Die Summe aller Residuen ergibt null.
• Der Mittelwert der Residuen ist null.

Wie werden Reststoffe in der Praxis verwendet?

In der Praxis werden Residuen bei der Regression aus drei verschiedenen Gründen verwendet:

1. Beurteilen Sie die Passform des Modells.

Sobald wir eine angepasste Regressionsgerade erstellt haben, können wir die Residuenquadratsumme (RSS) berechnen, die die Summe aller quadrierten Residuen ist. Je niedriger der RSS, desto besser passt das Regressionsmodell zu den Daten.

2. Überprüfen Sie die Annahme der Normalität.

Eine der wichtigsten Annahmen der linearen Regression ist, dass die Residuen normalverteilt sind.

Um diese Annahme zu überprüfen, können wir ein QQ-Diagramm erstellen, das eine Art Diagramm ist, mit dem wir bestimmen können, ob die Residuen eines Modells einer Normalverteilung folgen oder nicht.

Wenn die Punkte auf dem Diagramm grob eine gerade Diagonale bilden, ist die Normalitätsannahme erfüllt.

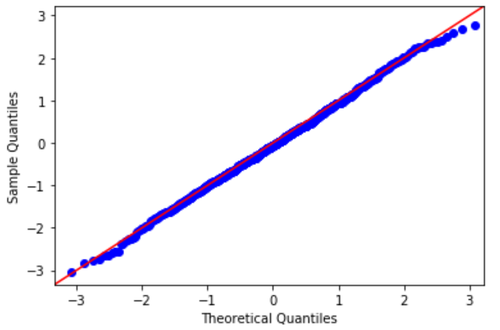
Beispiel für einen QQ-Plot

3. Überprüfen Sie die Annahme der Homoskedastizität.

Eine weitere wichtige Annahme der linearen Regression ist, dass die Residuen auf jeder Ebene von x eine konstante Varianz aufweisen. Dies wird als Homoskedastizität bezeichnet. Ist dies nicht der Fall, so spricht man von Heteroskedastizität.

Um zu überprüfen, ob diese Annahme erfüllt ist, können wir ein Residuendiagramm erstellen, bei dem es sich um ein Streudiagramm handelt, das die Residuen gegenüber den vorhergesagten Werten des Modells zeigt.

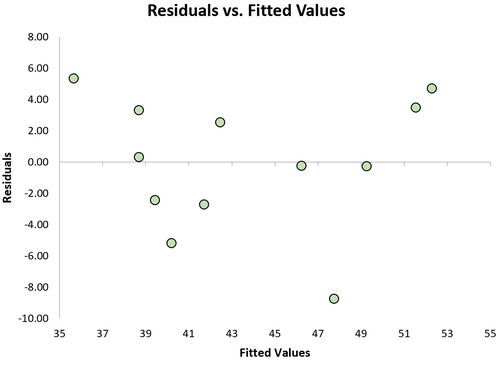
Beispiel für eine Darstellung von Residuen vs. angepassten Werten

Wenn die Residuen im Diagramm ohne klares Muster ungefähr gleichmäßig um Null gestreut sind, dann sagen wir normalerweise, dass die Annahme der Homoskedastizität erfüllt ist.

Zusätzliche Ressourcen

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
Die vier Annahmen der linearen Regression
So erstellen Sie ein Residualplot in Excel