Polynomiale Regression in Google Tabellen (Schritt für Schritt)

Die Regressionsanalyse wird verwendet, um die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu quantifizieren.

Die häufigste Art der Regressionsanalyse ist die einfache lineare Regression, die verwendet wird, wenn eine Prädiktorvariable und eine Antwortvariable eine lineare Beziehung aufweisen.

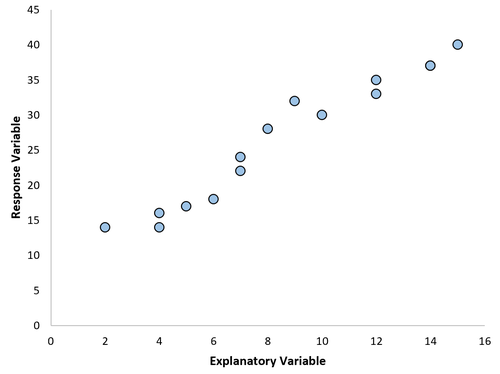
Manchmal ist die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen jedoch nicht linear.

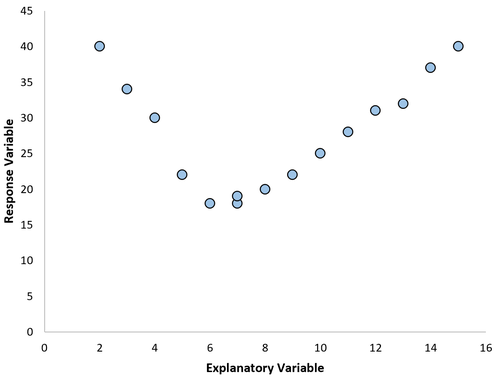
In diesen Fällen ist es sinnvoll, die polynomiale Regression zu verwenden, die den nichtlinearen Zusammenhang zwischen den Variablen berücksichtigen kann.

Dieses Tutorial enthält ein Schritt-für-Schritt-Beispiel zur Durchführung einer polynomialen Regression in Google Sheets

Schritt 1: Erstellen Sie die Daten

Lassen Sie uns zunächst einen gefälschten Datensatz mit den folgenden Werten erstellen:

Schritt 2: Erstellen Sie ein Streudiagramm

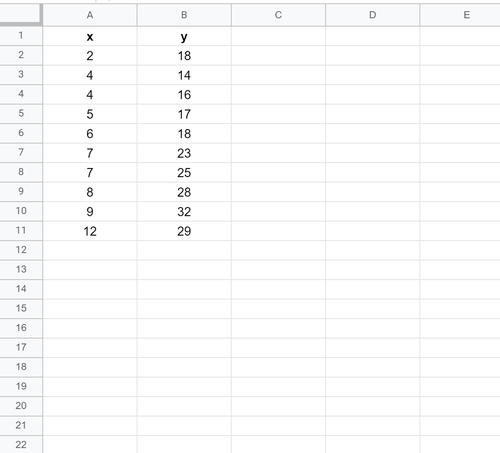
Als Nächstes erstellen wir ein Streudiagramm, um die Daten zu visualisieren.

Markieren Sie zuerst die Zellen A2:B11 wie folgt:

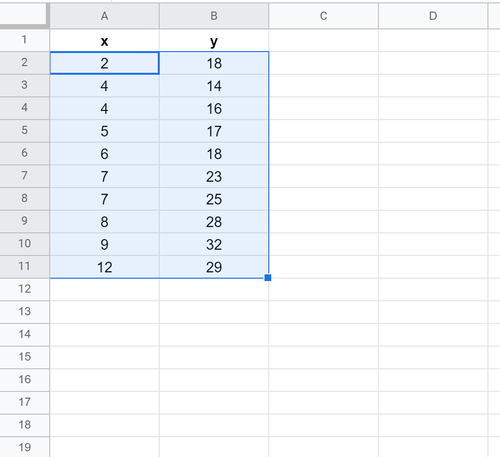
Klicken Sie als Nächstes auf die Registerkarte Einfügen und dann im Dropdown-Menü auf Diagramm:

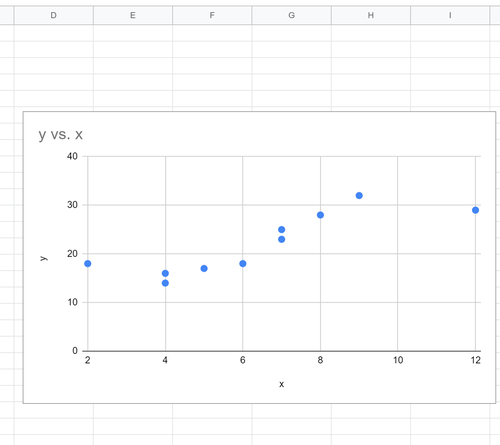
Standardmäßig fügt Google Tabellen ein Streudiagramm ein:

Schritt 3: Finden Sie die polynomiale Regressionsgleichung

Doppelklicken Sie als Nächstes auf eine beliebige Stelle im Streudiagramm, um das Diagrammeditorfenster auf der rechten Seite aufzurufen:

Klicken Sie als Nächstes auf Serie. Scrollen Sie dann nach unten und aktivieren Sie das Kontrollkästchen neben Trendline und ändern Sie den Typ in Polynomial. Wählen Sie für Label Use Equation und aktivieren Sie dann das Kontrollkästchen neben Show R ².

Dadurch wird die folgende Formel über dem Streudiagramm angezeigt:

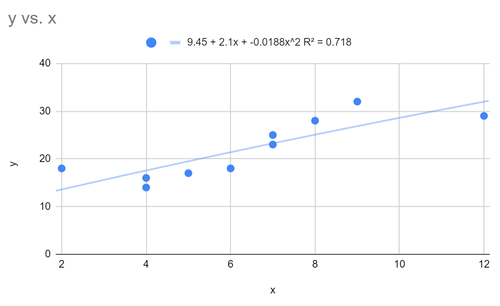
Wir können sehen, dass die angepasste polynomiale Regressionsgleichung lautet:

y = 9,45 + 2,1x – 0,0188x ²

Das R-Quadrat für dieses Modell beträgt 0,718.

Denken Sie daran, dass R-Quadrat uns den Prozentsatz der Variation in der Antwortvariablen angibt, die durch die Prädiktorvariablen erklärt werden kann. Je höher der Wert, desto besser das Modell.

Als nächstes ändern Sie den Grad des Polynoms im Diagrammeditor auf 3:

Dadurch wird die folgende Formel über dem Streudiagramm angezeigt:

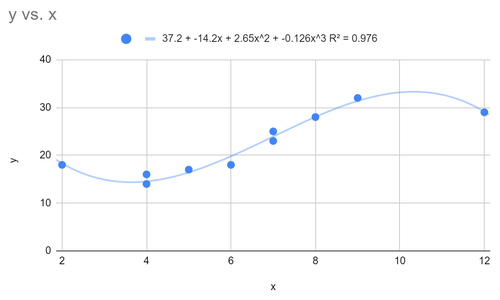
Dadurch ändert sich die angepasste polynomiale Regressionsgleichung zu:

y = 37,2 – 14,2x + 2,64x ² – 0,126x ³

Das R-Quadrat für dieses Modell beträgt 0,976.

Beachten Sie, dass das R-Quadrat für dieses Modell erheblich höher ist als das polynomiale Regressionsmodell mit einem Grad von 2. Dies deutet darauf hin, dass dieses Regressionsmodell den Trend in den zugrunde liegenden Daten erheblich besser erfassen kann.

Wenn Sie den Grad des Polynoms auf 4 ändern, steigt das R-Quadrat nur knapp auf 0,981. Dies deutet darauf hin, dass ein polynomiales Regressionsmodell mit einem Grad von 3 ausreicht, um den Trend für diese Daten zu erfassen.

Wir können die angepasste Regressionsgleichung verwenden, um den erwarteten Wert für die Antwortvariable basierend auf einem gegebenen Wert für die Prädiktorvariable zu finden. Wenn zum Beispiel x = 4 ist, wäre der erwartete Wert für y :

y = 37,2 – 14,2(4) + 2,64(4) ² – 0,126(4) ³ = 14,576

Weitere Google Tabellen-Tutorials finden Sie auf dieser Seite.