Durchführen einer logistischen Regression in Stata

Die logistische Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen, wenn die Antwortvariable binär ist. Hier sind einige Beispiele, wann wir logistische Regression verwenden können:

• Wir möchten wissen, wie sich Bewegung, Ernährung und Gewicht auf die Wahrscheinlichkeit eines Herzinfarkts auswirken. Die Antwortvariable ist heart attack und hat zwei mögliche Folgen: Ein Herzinfarkt tritt auf oder tritt nicht auf.
• Wir möchten wissen, wie sich GPA, ACT-Score und Anzahl der absolvierten AP-Klassen auf die Wahrscheinlichkeit auswirken, an einer bestimmten Universität aufgenommen zu werden. Die Antwortvariable ist acceptance und hat zwei mögliche Ergebnisse: akzeptiert oder nicht akzeptiert.
• Wir möchten wissen, ob die Anzahl der Wörter und der E-Mail-Titel die Wahrscheinlichkeit beeinflussen, dass eine E-Mail Spam ist. Die Antwortvariable ist spam und hat zwei mögliche Folgen: Spam oder nicht Spam.

In diesem Tutorial wird erläutert, wie Sie eine logistische Regression in Stata durchführen.

Beispiel: Logistische Regression in Stata

Angenommen, wir möchten verstehen, ob das Alter einer Mutter und ihre Rauchgewohnheiten die Wahrscheinlichkeit beeinflussen, ein Baby mit einem niedrigen Geburtsgewicht zu bekommen.

Um dies zu untersuchen, können wir eine logistische Regression durchführen, indem wir Alter und Rauchen (entweder Ja oder Nein) als erklärende Variablen und niedriges Geburtsgewicht (entweder Ja oder Nein) als Antwortvariable verwenden. Da die Antwortvariable binär ist – es gibt nur zwei mögliche Ergebnisse – ist es angebracht, die logistische Regression zu verwenden.

Führen Sie die folgenden Schritte in Stata aus, um eine logistische Regression mit dem Datensatz lbw durchzuführen, der Daten zu 189 verschiedenen Müttern enthält.

Schritt 1: Laden Sie die Daten.

Laden Sie die Daten, indem Sie Folgendes in das Befehlsfeld eingeben:

use http://www.stata-press.com/data/r13/lbw

Schritt 2: Holen Sie sich eine Zusammenfassung der Daten.

Machen Sie sich ein schnelles Bild von den Daten, mit denen Sie arbeiten, indem Sie Folgendes in das Befehlsfeld eingeben:

summarize

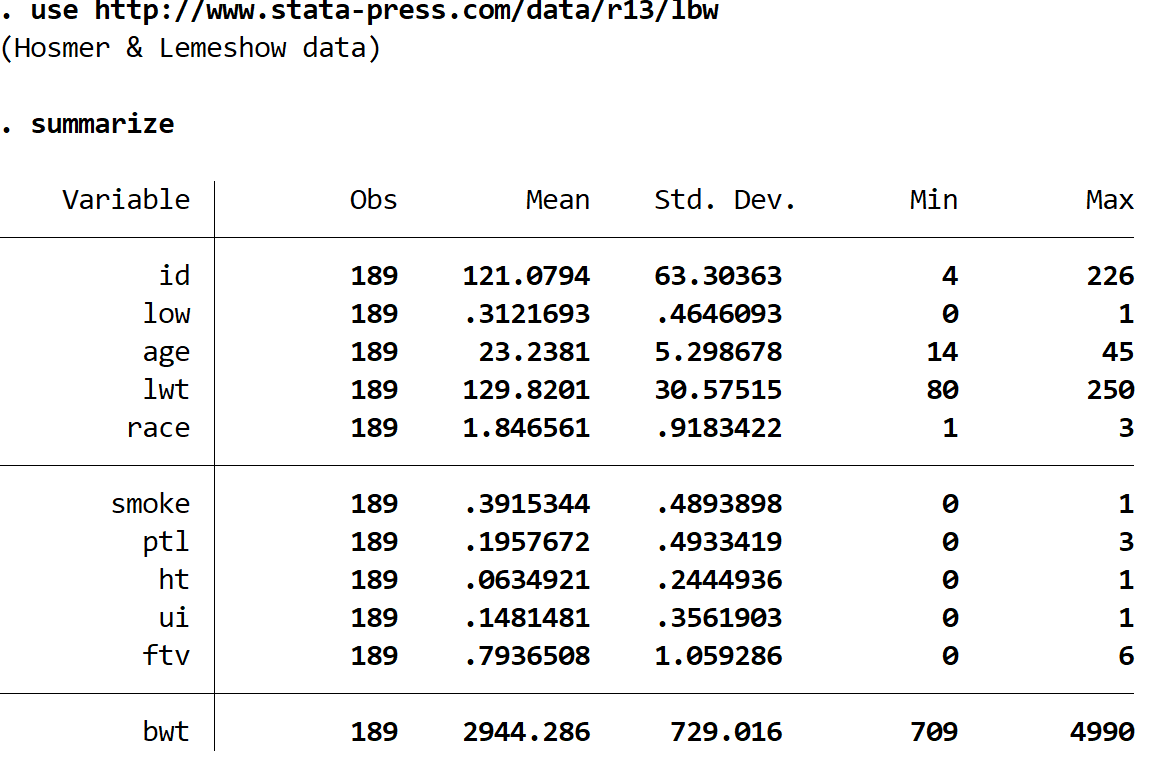
Wir können sehen, dass der Datensatz 11 verschiedene Variablen enthält, aber die einzigen drei, die uns interessieren, sind die folgenden:

• niedrig – ob das Baby ein niedriges Geburtsgewicht hatte oder nicht. 1 = ja, 0 = nein.
• Alter – Alter der Mutter.
• Rauch – ob die Mutter während der Schwangerschaft geraucht hat oder nicht. 1 = ja, 0 = nein.

Schritt 3: Führen Sie eine logistische Regression durch.

Geben Sie Folgendes in das Befehlsfeld ein, um eine logistische Regression durchzuführen, wobei age und smoke als erklärende Variablen und low als Antwortvariable verwendet werden.

logit low age smoke

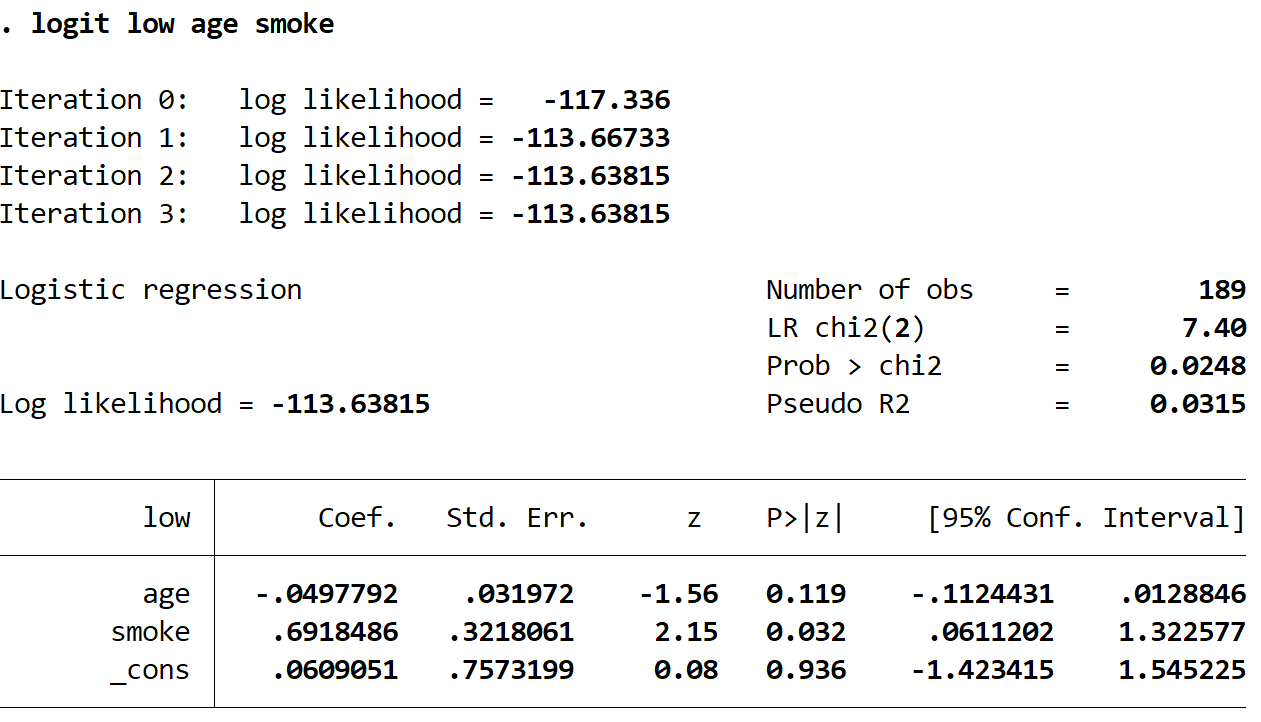
So interpretieren Sie die interessantesten Zahlen in der Ausgabe:

Coef (age): -.0497792. Wenn der Rauch konstant gehalten wird, ist jede Zunahme des Alters um ein Jahr mit einer Zunahme (-. 0497792) = 0,951 Zunahme der Wahrscheinlichkeit eines Babys mit niedrigem Geburtsgewicht verbunden. Da diese Zahl kleiner als 1 ist, bedeutet dies, dass eine Zunahme des Alters tatsächlich mit einer Abnahme der Wahrscheinlichkeit verbunden ist, ein Baby mit niedrigem Geburtsgewicht zu bekommen.

Angenommen, Mutter A und Mutter B sind beide Raucher. Wenn Mutter A ein Jahr älter als Mutter B ist, beträgt die Wahrscheinlichkeit, dass Mutter A ein Baby mit niedrigem Geburtsgewicht hat, nur 95,1% der Wahrscheinlichkeit, dass Mutter B ein Baby mit niedrigem Geburtsgewicht hat.

P> | z | (age): 0,119. Dies ist der p-Wert, der mit der Teststatistik für das Alter verknüpft ist. Da dieser Wert nicht weniger als 0,05 beträgt, ist das Alter kein statistisch signifikanter Prädiktor für ein niedriges Geburtsgewicht.

Quotenverhältnis (smoke): .6918486. Bei konstantem Alter (age) hat eine Mutter, die während der Schwangerschaft raucht, eine höhere Wahrscheinlichkeit (.6918486) = 1.997, ein Baby mit niedrigem Geburtsgewicht zu bekommen als eine Mutter, die während der Schwangerschaft nicht raucht.

Angenommen, Mutter A und Mutter B sind beide 30 Jahre alt. Wenn Mutter A während der Schwangerschaft raucht und Mutter B nicht, ist die Wahrscheinlichkeit, dass Mutter A ein Baby mit niedrigem Geburtsgewicht hat, um 99,7% höher als die Wahrscheinlichkeit, dass Mutter B ein Baby mit niedrigem Geburtsgewicht hat.

P> | z | (smoke): 0,032. Dies ist der p-Wert, der mit der Teststatistik für smoke verknüpft ist. Da dieser Wert weniger als 0,05 beträgt, ist smoke ein statistisch signifikanter Prädiktor für ein niedriges Geburtsgewicht.

Schritt 4: Reporten Sie die Ergebnisse.

Zuletzt möchten wir die Ergebnisse unserer logistischen Regression melden. Hier ist ein Beispiel dafür:

Eine logistische Regression wurde durchgeführt, um festzustellen, ob das Alter einer Mutter und ihre Rauchgewohnheiten die Wahrscheinlichkeit beeinflussen, ein Baby mit einem niedrigen Geburtsgewicht zu bekommen. Bei der Analyse wurde eine Stichprobe von 189 Müttern verwendet.

Die Ergebnisse zeigten, dass es eine statistisch signifikante Beziehung zwischen Rauchen und Wahrscheinlichkeit eines niedrigen Geburtsgewichts gab (z = 2,15, p = 0,032), während es keine statistisch signifikante Beziehung zwischen Alter und Wahrscheinlichkeit eines niedrigen Geburtsgewichts gab (z = -1,56, p =). 119).