Einführung in die logistische Regression

Wenn wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer kontinuierlichen Antwortvariablen verstehen wollen, verwenden wir häufig eine lineare Regression.

Wenn die Antwortvariable jedoch kategorisch ist, können wir stattdessen die logistische Regression verwenden.

Die logistische Regression ist eine Art Klassifizierungsalgorithmus, da versucht wird, Beobachtungen aus einem Datensatz in verschiedene Kategorien zu „klassifizieren“.

Hier einige Beispiele, wann wir die logistische Regression verwenden könnten:

• Wir möchten die Kreditwürdigkeit und das Bankguthaben verwenden, um vorherzusagen, ob ein bestimmter Kunde einen Kredit nicht in Anspruch nimmt oder nicht. (Antwortvariable = "Standard" oder "Kein Standard")
• Wir möchten durchschnittliche Rebounds pro Spiel und durchschnittliche Punkte pro Spiel verwenden, um vorherzusagen, ob ein bestimmter Basketballspieler in die NBA eingezogen wird oder nicht (Antwortvariable = "Drafted" oder "Not Drafted").
• Wir möchten anhand der Fläche und der Anzahl der Badezimmer vorhersagen, ob ein Haus in einer bestimmten Stadt zu einem Verkaufspreis von 200.000 USD oder mehr angeboten wird. (Antwortvariable = "Ja" oder "Nein")

Beachten Sie, dass die Antwortvariable in jedem dieser Beispiele nur einen von zwei Werten annehmen kann. Vergleichen Sie dies mit der linearen Regression, bei der die Antwortvariable einen kontinuierlichen Wert annimmt.

Die logistische Regressionsgleichung

Die logistische Regression verwendet eine Methode, die als Maximum-Likelihood-Schätzung bekannt ist (Details werden hier nicht behandelt), um eine Gleichung der folgenden Form zu finden:

log [p (X) / (1-p (X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ +… + β _p X _p

wo:

• X _j: Die j-te Prädiktorvariable
• β _j: Die Koeffizientenschätzung für die j-te Prädiktorvariable

Die Formel auf der rechten Seite der Gleichung sagt die logarithmische Wahrscheinlichkeit voraus, dass die Antwortvariable einen Wert von 1 annimmt.

Wenn wir also ein logistisches Regressionsmodell anpassen, können wir die folgende Gleichung verwenden, um die Wahrscheinlichkeit zu berechnen, dass eine bestimmte Beobachtung einen Wert von 1 annimmt:

p (X) = e ^{& bgr; ₀ + & bgr; ₁ X ₁ + & bgr; ₂ X ₂ +… + & bgr; _p X _p} / (1 + e ^{& bgr; ₀ + & bgr; ₁ X ₁ + & bgr; ₂ X ₂ +… + & bgr; _p X _p} )

Wir verwenden dann einen Wahrscheinlichkeitsschwellenwert, um die Beobachtung entweder als 1 oder als 0 zu klassifizieren.

Zum Beispiel könnten wir sagen, dass Beobachtungen mit einer Wahrscheinlichkeit größer oder gleich 0,5 als „1“ und alle anderen Beobachtungen als „0“ klassifiziert werden.

Interpretieren der logistischen Regressionsausgabe

Angenommen, wir verwenden ein logistisches Regressionsmodell, um vorherzusagen, ob ein bestimmter Basketballspieler basierend auf seinen durchschnittlichen Rebounds pro Spiel und den durchschnittlichen Punkten pro Spiel in die NBA eingezogen wird oder nicht.

Hier ist die Ausgabe für das logistische Regressionsmodell:

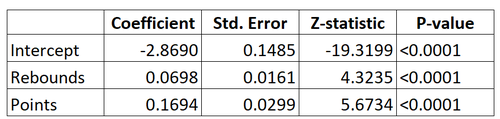
Unter Verwendung der Koeffizienten können wir die Wahrscheinlichkeit, dass ein bestimmter Spieler in die NBA eingezogen wird, basierend auf seinen durchschnittlichen Rebounds und Punkten pro Spiel unter Verwendung der folgenden Formel berechnen:

P(Entwurf) = e ^{-2,8690 + 0,0698 * (Rebs) + 0,1694 * (Punkte)} / (1 + e ^{-2,8690 + 0,0698 * (Rebs) + 0,1694 * (Punkte)} )

Angenommen, ein bestimmter Spieler erzielt durchschnittlich 8 Rebounds pro Spiel und 15 Punkte pro Spiel. Nach dem Modell beträgt die Wahrscheinlichkeit, dass dieser Spieler in die NBA eingezogen wird, 0,557.

P(Entwurf) = e ^{-2,8690 + 0,0698 * (8) + 0,1694 * (15)} / (1 + e ^{-2,8690 + 0,0698 * (8) + 0,1694 * (15)} ) = 0,557

Da diese Wahrscheinlichkeit größer als 0,5 ist, würden wir vorhersagen, dass dieser Spieler eingezogen wird.

Vergleichen Sie dies mit einem Spieler, der durchschnittlich nur 3 Rebounds und 7 Punkte pro Spiel erzielt. Die Wahrscheinlichkeit, dass dieser Spieler in die NBA eingezogen wird, beträgt 0,186.

P(Entwurf) = e ^{-2,8690 + 0,0698 * (3) + 0,1694 * (7)} / (1 + e ^{-2,8690 + 0,0698 * (3) + 0,1694 * (7)} ) = 0,186

Da diese Wahrscheinlichkeit weniger als 0,5 beträgt, würden wir vorhersagen, dass dieser Spieler nicht eingezogen wird.

Annahmen der logistischen Regression

Die logistische Regression verwendet die folgenden Annahmen:

1. Die Antwortvariable ist binär. Es wird angenommen, dass die Antwortvariable nur zwei mögliche Ergebnisse annehmen kann.

2. Die Beobachtungen sind unabhängig. Es wird angenommen, dass die Beobachtungen im Datensatz unabhängig voneinander sind. Das heißt, die Beobachtungen sollten nicht aus wiederholten Messungen desselben Individuums stammen oder in irgendeiner Weise miteinander in Beziehung stehen.

3. Es gibt keine schwerwiegende Multikollinearität zwischen Prädiktorvariablen. Es wird angenommen, dass keine der Prädiktorvariablen stark miteinander korreliert ist.

4. Es gibt keine extremen Ausreißer. Es wird davon ausgegangen, dass der Datensatz keine extremen Ausreißer oder einflussreichen Beobachtungen enthält.

5. Es besteht eine lineare Beziehung zwischen den Prädiktorvariablen und dem Logit der Antwortvariablen. Diese Annahme kann mit einem Box-Tidwell-Test überprüft werden.

6. Die Stichprobengröße ist ausreichend groß. Als Faustregel sollten Sie mindestens 10 Fälle mit dem seltensten Ergebnis für jede erklärende Variable haben. Wenn Sie beispielsweise 3 erklärende Variablen haben und die erwartete Wahrscheinlichkeit für das am wenigsten häufige Ergebnis 0,20 beträgt, sollten Sie eine Stichprobengröße von mindestens (10 * 3) / 0,20 = 150 haben.

In diesem Beitrag finden Sie eine ausführliche Erläuterung zur Überprüfung dieser Annahmen.