Was ist das Latin Hypercube Stichprobenverfahren?

Das Latin Hypercube Stichprobenverfahren ist eine Methode, die zur Stichprobenziehung von Zufallszahlen verwendet werden kann, bei der die Stichproben gleichmäßig über einen Stichprobenraum verteilt sind.

Es wird häufig verwendet, um Stichproben zu erzeugen, die als kontrollierte Zufallsstichproben bekannt sind, und wird häufig in der Monte-Carlo-Analyse eingesetzt, da es die Anzahl der für genaue Ergebnisse erforderlichen Simulationen drastisch reduzieren kann.

Einführendes Beispiel

Um die Idee der Latin-Hypercube-Stichprobe zu verstehen, betrachten Sie das folgende einfache Beispiel:

Angenommen, wir möchten eine Stichprobe von 2 Werten aus einem normalverteilten Datensatz mit einem Mittelwert von 0 und einer Standardabweichung von 1 erhalten.

Wenn wir einen echten Zufallszahlengenerator verwenden, um diese Stichprobe zu erhalten, ist es möglich, dass beide Werte größer als 0 sind oder dass beide Werte kleiner als 0 sind.

Wenn wir jedoch eine Latin-Hypercube-Stichprobe verwenden würden, um diese Stichprobe zu erhalten, dann wäre garantiert, dass ein Wert über 0 und einer unter 0 liegt, da wir den Stichprobenraum gezielt in eine Region mit Werten über 0 und eine Region mit Werten unter 0 unterteilen und dann aus jeder Region eine Zufallsstichprobe auswählen könnten.

Eindimensionales Latin Hypercube Stichprobenverfahren

Die Idee hinter der eindimensionalen Latin-Hypercube-Stichprobe ist einfach: Man unterteilt eine gegebene CDF (kumulative Verteilungsfunktion) in n verschiedene Regionen und wählt zufällig einen Wert aus jeder Region aus, um eine Stichprobe der Größe n zu erhalten.

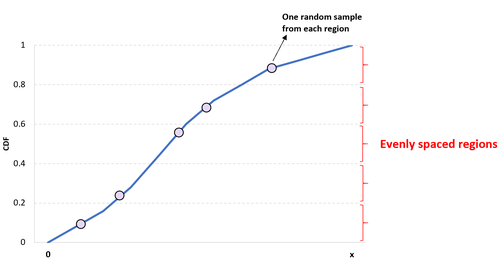
Der Vorteil dieses Ansatzes ist, dass er sicherstellt, dass mindestens ein Wert aus jeder Region in die Stichprobe aufgenommen wird.

Zweidimensionales Latin Hypercube Stichprobenverfahren

Wir können die Idee des eindimensionalen Latin-Hypercube-Stichprobenverfahrens auch leicht auf zwei Dimensionen ausweiten.

Für zwei Variablen, x und y, können wir den Stichprobenraum jeder Variablen in n gleichmäßig beabstandete Regionen unterteilen und aus jedem Stichprobenraum eine Zufallsstichprobe ziehen, um Zufallswerte über zwei Dimensionen hinweg zu erhalten.

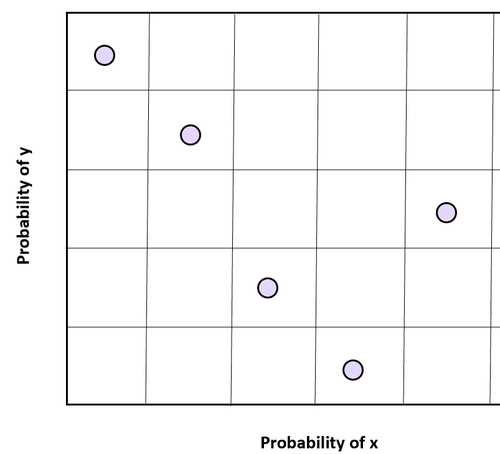
Es ist wichtig zu beachten, dass die beiden Variablen unabhängig sein müssen, damit diese Stichprobentechnik die gewünschten Ergebnisse erzielt.

N-Dimensionales Latin Hypercube Stichprobenverfahren

Um Latin Hypercube Stichprobenverfahren in größeren Dimensionen durchzuführen, können wir die Idee des zweidimensionalen Latin Hypercube Stichprobenverfahrens einfach auf noch mehr Dimensionen ausdehnen.

Jede Variable wird einfach in gleichmäßig verteilte Regionen aufgeteilt und aus jeder Region werden dann Zufallsstichproben gezogen, um eine kontrollierte Zufallsstichprobe zu erhalten.

Verwandt: Was sind hochdimensionale Daten?

Warum Latin Hypercube Stichprobenverfahren verwenden?

Der Hauptvorteil der Latin-Hypercube-Stichprobe besteht darin, dass sie Stichproben erzeugt, die die tatsächliche zugrundeliegende Verteilung widerspiegeln, und dass sie in der Regel einen viel geringeren Stichprobenumfang erfordert als einfache Zufallsstichproben.

Diese Methode der Stichprobenziehung kann besonders vorteilhaft sein, wenn Sie mit Daten arbeiten, die eine hohe Anzahl von Dimensionen aufweisen, und wenn Sie Stichproben benötigen, die mit Sicherheit die tatsächliche zugrunde liegende Verteilung der Daten widerspiegeln.