Hauptkomponentenanalyse in R: Schritt-für-Schritt-Beispiel

Die Hauptkomponentenanalyse, oft als PCA (engl. Principal Component Analysis) abgekürzt, ist eine unüberwachte maschinelle Lerntechnik, mit der versucht wird, Hauptkomponenten - lineare Kombinationen der ursprünglichen Prädiktoren - zu finden, die einen großen Teil der Variation in einem Datensatz erklären.

Das Ziel von PCA ist es, den größten Teil der Variabilität in einem Datensatz mit weniger Variablen als dem ursprünglichen Datensatz zu erklären.

Für einen gegebenen Datensatz mit p Variablen könnten wir die Streudiagramme jeder paarweisen Kombination von Variablen untersuchen, aber die bloße Anzahl von Streudiagrammen kann sehr schnell groß werden.

Für p Prädiktoren gibt es p(p-1)/2 Streudiagramme.

Für einen Datensatz mit p = 15 Prädiktoren gäbe es also 105 verschiedene Streudiagramme!

Glücklicherweise bietet PCA eine Möglichkeit, eine niedrigdimensionale Darstellung eines Datensatzes zu finden, die so viele Variationen der Daten wie möglich erfasst.

Wenn wir den größten Teil der Variation in nur zwei Dimensionen erfassen können, können wir alle Beobachtungen im Originaldatensatz auf ein einfaches Streudiagramm projizieren.

Wir finden die Hauptkomponenten folgendermaßen:

Berechnen Sie bei einem Datensatz mit p Prädiktoren: X ₁ , X ₂ ,…, X _p ,, Z ₁ ,…, Z _M als die M linearen Kombinationen der ursprünglichen p Prädiktoren, wobei:

• Z _m = ΣΦ _jm X _j für einige Konstanten Φ _1m , Φ _2m , Φ _pm , m = 1,…, M.
• Z ₁ ist die lineare Kombination der Prädiktoren, die die größtmögliche Varianz erfasst.
• Z ₂ ist die nächste lineare Kombination der Prädiktoren, die die größte Varianz erfasst, während sie orthogonal (d.h. nicht korreliert) zu Z ₁ ist.
• Z ₃ ist dann die nächste lineare Kombination der Prädiktoren, die die größte Varianz erfasst, während sie orthogonal zu Z _{2 ist}.
• Und so weiter.

In der Praxis verwenden wir die folgenden Schritte, um die linearen Kombinationen der ursprünglichen Prädiktoren zu berechnen:

1. Skalieren Sie jede der Variablen auf einen Mittelwert von 0 und eine Standardabweichung von 1.

2. Berechnen Sie die Kovarianzmatrix für die skalierten Variablen.

3. Berechnen Sie die Eigenwerte der Kovarianzmatrix.

Mit Hilfe der linearen Algebra kann gezeigt werden, dass der Eigenvektor, der dem größten Eigenwert entspricht, die erste Hauptkomponente ist. Mit anderen Worten, diese spezielle Kombination der Prädiktoren erklärt die größte Varianz in den Daten.

Der dem zweitgrößten Eigenwert entsprechende Eigenvektor ist die zweite Hauptkomponente und so weiter.

Dieses Tutorial enthält ein schrittweises Beispiel für die Durchführung dieses Prozesses in R

Schritt 1: Laden Sie die Daten

Zuerst laden wir das tidyverse-Paket, das mehrere nützliche Funktionen zum Visualisieren und Bearbeiten von Daten enthält:

library(tidyverse)

In diesem Beispiel verwenden wir den in R integrierten Datensatz USArrests, der die Anzahl der Festnahmen pro 100.000 Einwohner in jedem US-Bundesstaat im Jahr 1973 für Mord, Überfall und Vergewaltigung enthält.

Es enthält auch den Prozentsatz der Bevölkerung in jedem Staat, die in städtischen Gebieten lebt, UrbanPop.

Der folgende Code zeigt, wie die ersten Zeilen des Datasets geladen und angezeigt werden:

#lade Daten
data("USArrests")

# Die ersten sechs Datenzeilen anzeigen
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama      13.2     236       58 21.2
Alaska       10.0     263       48 44.5
Arizona       8.1     294       80 31.0
Arkansas      8.8     190       50 19.5
California    9.0     276       91 40.6
Colorado      7.9     204       78 38.7

Schritt 2: Berechnen Sie die Hauptkomponenten

Nach dem Laden der Daten können wir die in R integrierte Funktion prcomp() verwenden, um die Hauptkomponenten des Datensatzes zu berechnen.

Stellen Sie sicher, dass scale = TRUE angegeben wird, damit jede der Variablen im Datensatz auf einen Mittelwert von 0 und eine Standardabweichung von 1 skaliert wird, bevor Sie die Hauptkomponenten berechnen.

Beachten Sie auch, dass Eigenvektoren in R standardmäßig in die negative Richtung zeigen, sodass wir mit -1 multiplizieren, um die Vorzeichen umzukehren.

# Hauptkomponenten berechnen
results <- prcomp(USArrests, scale = TRUE)

# die Vorzeichen umkehren
results$rotation <- -1*results$rotation

# Hauptkomponenten anzeigen
results$rotation

               PC1        PC2        PC3         PC4
Murder   0.5358995 -0.4181809  0.3412327 -0.64922780
Assault  0.5831836 -0.1879856  0.2681484  0.74340748
UrbanPop 0.2781909  0.8728062  0.3780158 -0.13387773
Rape     0.5434321  0.1673186 -0.8177779 -0.08902432

Wir können sehen, dass die erste Hauptkomponente (PC1) hohe Werte für Mord, Körperverletzung und Vergewaltigung aufweist, was darauf hinweist, dass diese Hauptkomponente die größte Variation dieser Variablen beschreibt.

Wir können auch sehen, dass die zweite Hauptkomponente (PC2) einen hohen Wert für UrbanPop hat, was darauf hinweist, dass diese Hauptkomponente den größten Schwerpunkt auf die städtische Bevölkerung legt.

Beachten Sie, dass die Bewertungen der Hauptkomponenten für jeden Status in results$x gespeichert sind. Wir werden diese Werte auch mit -1 multiplizieren, um die Vorzeichen umzukehren:

#die Vorzeichen umkehren
results$x <- -1*results$x

#Die ersten sechs Punkte anzeigen
head(results$x)

                  PC1        PC2         PC3          PC4
Alabama     0.9756604 -1.1220012  0.43980366 -0.154696581
Alaska      1.9305379 -1.0624269 -2.01950027  0.434175454
Arizona     1.7454429  0.7384595 -0.05423025  0.826264240
Arkansas   -0.1399989 -1.1085423 -0.11342217  0.180973554
California  2.4986128  1.5274267 -0.59254100  0.338559240
Colorado    1.4993407  0.9776297 -1.08400162 -0.001450164

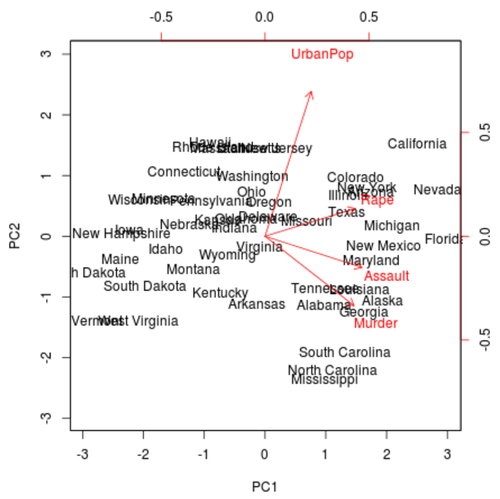
Schritt 3: Visualisieren Sie die Ergebnisse mit einem Biplot

Als nächstes können wir ein Biplot erstellen - ein Diagramm, das jede der Beobachtungen im Datensatz auf ein Streudiagramm projiziert, das die erste und die zweite Hauptkomponente als Achsen verwendet:

Beachten Sie, dass scale = 0 sicherstellt, dass die Pfeile im Diagramm skaliert werden, um die Belastungen darzustellen.

biplot(results, scale = 0)

Aus der Darstellung können wir jeden der 50 Zustände in einem einfachen zweidimensionalen Raum sehen.

Die Zustände, die im Diagramm nahe beieinander liegen, weisen ähnliche Datenmuster in Bezug auf die Variablen im Originaldatensatz auf.

Wir können auch sehen, dass bestimmte Staaten stärker mit bestimmten Verbrechen verbunden sind als andere. Zum Beispiel ist Georgia der Staat, der der Variablen Mord im Diagramm am nächsten kommt.

Wenn wir uns die Staaten mit den höchsten Mordraten im Originaldatensatz ansehen, können wir sehen, dass Georgien tatsächlich ganz oben auf der Liste steht:

#Anzeigen der Staaten mit den höchsten Mordraten im Originaldatensatz
head(USArrests[order(-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia          17.4     211       60 25.8
Mississippi      16.1     259       44 17.1
Florida          15.4     335       80 31.9
Louisiana        15.4     249       66 22.2
South Carolina   14.4     279       48 22.5
Alabama          13.2     236       58 21.2

Schritt 4: Finden Sie die Varianz, die von jeder Hauptkomponente erklärt wird

Wir können den folgenden Code verwenden, um die Gesamtvarianz im Originaldatensatz zu berechnen, die von jeder Hauptkomponente erklärt wird:

#Berechnen Sie die Gesamtvarianz, die von jeder Hauptkomponente erklärt wird
results$sdev^2 / sum(results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

Aus den Ergebnissen können wir Folgendes beobachten:

• Die erste Hauptkomponente erklärt 62% der Gesamtvarianz im Datensatz.
• Die zweite Hauptkomponente erklärt 24,7% der Gesamtvarianz im Datensatz.
• Die dritte Hauptkomponente erklärt 8,9% der Gesamtvarianz im Datensatz.
• Die vierte Hauptkomponente erklärt 4,3% der Gesamtvarianz im Datensatz.

Somit erklären die ersten beiden Hauptkomponenten einen Großteil der Gesamtvarianz in den Daten.

Dies ist ein gutes Zeichen, da der vorherige Biplot jede der Beobachtungen aus den Originaldaten auf ein Streudiagramm projizierte, das nur die ersten beiden Hauptkomponenten berücksichtigte.

Daher ist es gültig, Muster im Biplot zu betrachten, um Zustände zu identifizieren, die einander ähnlich sind.

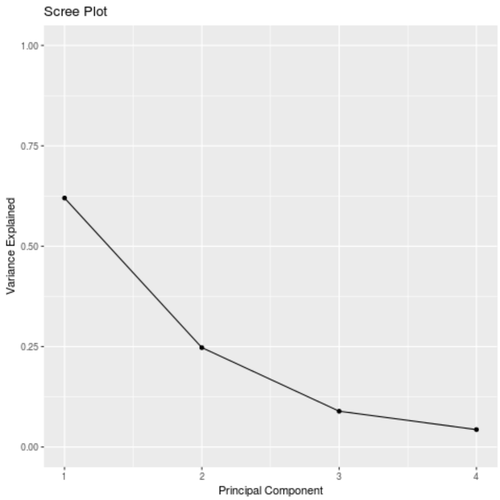
Wir können auch ein Scree Diagramm erstellen - ein Diagramm, das die von jeder Hauptkomponente erklärte Gesamtvarianz anzeigt -, um die Ergebnisse der PCA zu visualisieren:

#Berechnen Sie die Gesamtvarianz, die von jeder Hauptkomponente erklärt wird
var_explained = results$sdev^2 / sum(results$sdev^2)

# Screen Diagramm erstellen
qplot(c(1:4), var_explained) + 
 geom_line() + 
 xlab(" Principal Component") + 
 ylab(" Variance Explained") +
 ggtitle(" Scree Plot") +
 ylim(0, 1)

Hauptkomponentenanalyse in der Praxis

In der Praxis wird PCA aus zwei Gründen am häufigsten verwendet:

1. Explorative Datenanalyse - Wir verwenden PCA, wenn wir zum ersten Mal einen Datensatz untersuchen, und verstehen wollen, welche Beobachtungen in den Daten einander am ähnlichsten sind.

2. Regression der Hauptkomponenten - Wir können PCA auch verwenden, um Hauptkomponenten zu berechnen, die dann bei der Regression der Hauptkomponenten verwendet werden können. Diese Art der Regression wird häufig verwendet, wenn zwischen Prädiktoren in einem Datensatz Multikollinearität besteht.

Den vollständigen R-Code, der in diesem Tutorial verwendet wird, finden Sie hier.